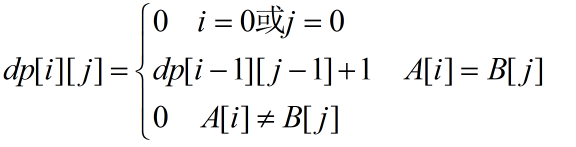dp求解各种子串子序列
注:dp可能并不是求解该这些问题的最优算法,这里只是做一个dp 算法的简介。
概念
定义:假设现有一个 string = abcdefghijklmn
最长连续子串:要求在原序列中连续,比如 str = abcd、fghijklm都是valid substring
最长连续子序列:相对顺序在原序列中不变即可;比如 str = afgh、dfkn等等都是valid subsequence
说完了上面的定义;下面来说一说怎么用dp求解最长连续子串和最长连续子序列;既然用到了dp 的方法求解,就要找出相关的状态转移方程。
最长上升子序列
#include <bits/stdc++.h>
using namespace std;
const int maxn=3e4+10;
int a[maxn],b[maxn],n;
int dp[maxn],ans; //dp[i]表示前i个的最长上升子序列
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
dp[i]=1;
for(int j=1;j<i;++j){
if(a[j]<a[i]&&b[j]<b[i]) dp[i]=max(dp[i],dp[j]+1);
ans=max(ans,dp[i]);
}
}
printf("%d\n",ans);
system("pause");
}
最长连续子串
递推方程:
int f[maxn][maxn];
int solve(char *x, char *y)
{
int ans=0;
int lenx=strlen(x);
int leny=strlen(y);
for (int i=0;i<lenx;i++)
{
for (int j=0;j<leny;j++){
if (x[i]!=y[j]) f[i][j]=0;
else if(x[i]==y[j]) f[i][j]=f[i-1][j-1]+1;
ans=max(ans,f[i][j]);
}
}
return ans;
}
最长公共子序列
状态转移方程:
模板(花里胡哨的dp请忽略,网上版本,也可成二维数组):
int dp[maxn][maxn]; //a[1]~a[i]与b[1]~b[j]的最长公共子序列
int solve(int n,int m)
{
for (int i=0;i<=n;i++) dp[i][0] = 0;
for (int i=0;i<=m;i++) dp[0][i] = 0;
for (int i=1;i<=n;i++){ //n,m分别为两个数组的长度
for (int j=1;j<=m;j++){
if (a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[n][m];
}
最长公共上升子序列
dp[i][j]的含义同最长公共子序列;
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn=3e3+10;
int a[maxn],b[maxn];
int dp[maxn][maxn]; //表示a[1]~a[i]与b[1]~b[j]且以b[j]为结尾的最长上升公共子序列
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(a[i]==b[j]){
dp[i][j]=1;
for(int k=1;k<j;++k){
if(b[k]<a[i]) dp[i][j]=max(dp[i][j],dp[i-1][k]+1);
}
}
else dp[i][j]=dp[i-1][j];
}
}
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,dp[n][i]);
printf("%d\n",ans);
system("pause");
}
上面是未优化前的代码;起代码复杂度未O(n^3);其中的k循环可以被优化;优化后时间复杂度为O(n^2),看代码:
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn=3e3+10;
int a[maxn],b[maxn];
int dp[maxn][maxn]; //表示a[1]~a[i]与b[1]~b[j]且以b[j]为结尾的最长上升公共子序列
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
int maxv=1;
for(int j=1;j<=n;++j){
dp[i][j]=dp[i-1][j];
if(a[i]==b[j]) dp[i][j]=max(dp[i][j],maxv);
if(b[j]<a[i]) maxv=max(maxv,dp[i][j]+1);
}
}
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,dp[n][i]);
printf("%d\n",ans);
system("pause");
}
dp求解各种子串子序列的更多相关文章
- DP——最长上升子序列(LIS)
DP——最长上升子序列(LIS) 基本定义: 一个序列中最长的单调递增的子序列,字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符,即可以去掉字符串中的部分字符,但不可改变其前后顺序. LIS ...
- HDU 1087 简单dp,求递增子序列使和最大
Super Jumping! Jumping! Jumping! Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 ...
- hdu 1025 dp 最长上升子序列
//Accepted 4372 KB 140 ms //dp 最长上升子序列 nlogn #include <cstdio> #include <cstring> #inclu ...
- LeetCode OJ 322. Coin Change DP求解
题目链接:https://leetcode.com/problems/coin-change/ 322. Coin Change My Submissions Question Total Accep ...
- 动态规划(Dynamic Programming, DP)---- 最大连续子序列和
动态规划(Dynamic Programming, DP)是一种用来解决一类最优化问题的算法思想,简单来使,动态规划是将一个复杂的问题分解成若干个子问题,或者说若干个阶段,下一个阶段通过上一个阶段的结 ...
- uva 10069 Distinct Subsequences(高精度 + DP求解子串个数)
题目连接:10069 - Distinct Subsequences 题目大意:给出两个字符串x (lenth < 10000), z (lenth < 100), 求在x中有多少个z. ...
- 算法练习--- DP 求解最长上升子序列(LIS)
问题描写叙述: 对于2,5,3,1,9,4,6,8,7,找出最长上升子序列的个数 最长上升子序列定义: 对于i<j i,j∈a[0...n] 满足a[i]<a[j] 1. 找出DP公式:d ...
- 洛谷 P1020 导弹拦截(dp+最长上升子序列变形)
传送门:Problem 1020 https://www.cnblogs.com/violet-acmer/p/9852294.html 讲解此题前,先谈谈何为最长上升子序列,以及求法: 一.相关概念 ...
- HDU 4632 Palindrome subsequence(区间DP求回文子序列数)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4632 题目大意:给你若干个字符串,回答每个字符串有多少个回文子序列(可以不连续的子串).解题思路: 设 ...
随机推荐
- 为什么Oracle等数据库软件可以同时创建多个连接
首先我们要明确的是一个IP跟一个端口确定的是一个进程的地址,也就是我们运行了一个Oracle的数据库,这时候就已经确定的了. oracle监听器也是一个TCP/IP网络中的进程,默认的端口号是1521 ...
- dw 快捷键
<html></html> 创建一个HTML文档<head></head> 设置文档标题和其它在网页中不显示的信息<title></t ...
- HADOOP_SECURE_DN_USER has been replaced by HDFS_DATANODE_SECURE_USER
这个问题可能是我第一个遇到吧,hadoop启动时WARNING: HADOOP_SECURE_DN_USER has been replaced by HDFS_DATANODE_SECURE_USE ...
- [Reversal 剧情设计] 设定
在正式写之前,先交代一些设定,便于后续的展开.先在这里说明一点,我的文笔可能很烂(因为在写小说方面还没有得到过别人的评价),只要你们能体会我想表达的东西就行(不过也的确是这样,如果作者构筑得过于详细, ...
- 作业2:go实现一个压测工具,具备upload功能
作业:go实现压测工具,具备upload功能. upload内容是.tar.gz,使用http协议上传. 要求:upload的文件名,http目的地址灵活可配. deadline:2019.4.30
- JS高级---体会面向对象和面向过程的编程思想
体会面向对象和面向过程的编程思想 ChangeStyle是自定义的构造函数,再通过原型添加方法的函数. 实例化对象,导入json参数,和创建cs,调用原型添加的方法函数 过渡,先熟悉记忆 <!D ...
- 神奇的requestAnimationFrame解决传统定时器bug
可能你还没见过这个东西是个啥,其实他就是类似于setTimeout和setInterval,然而它与setTimeout和setInterval又有所不同,requestAnimationFrame不 ...
- Apache Shiro——初识
Shrio是什么? Shrio是一个用Java开发的安全框架,用来保证系统或系统数据安全的.他可以用在大多数程序上,比如移动应用程序.Web程序或者大型的企业应用程序等. Shrio能干什么? 能用来 ...
- 脚本中的random几率问题详解
random解释: 没有固定数值,随即给的意思,数值越大就几率越低,跟爆率也不多,如下脚本,所有都抽不到的话,就会执行最后面没有检测条件的那个. [@main] #if random 10 #ac ...
- 「CF858F」 Wizard's Tour
传送门 Luogu 解题思路 首先对于树的情况,我们很显然有一种贪心策略: 对于每一个节点先匹配子树,然后在还可以匹配的儿子间尽可能匹配,要是多出来一个就往上匹配. 推广到图的情况... 我们在图的生 ...