F.Three pahs on a tree

思路

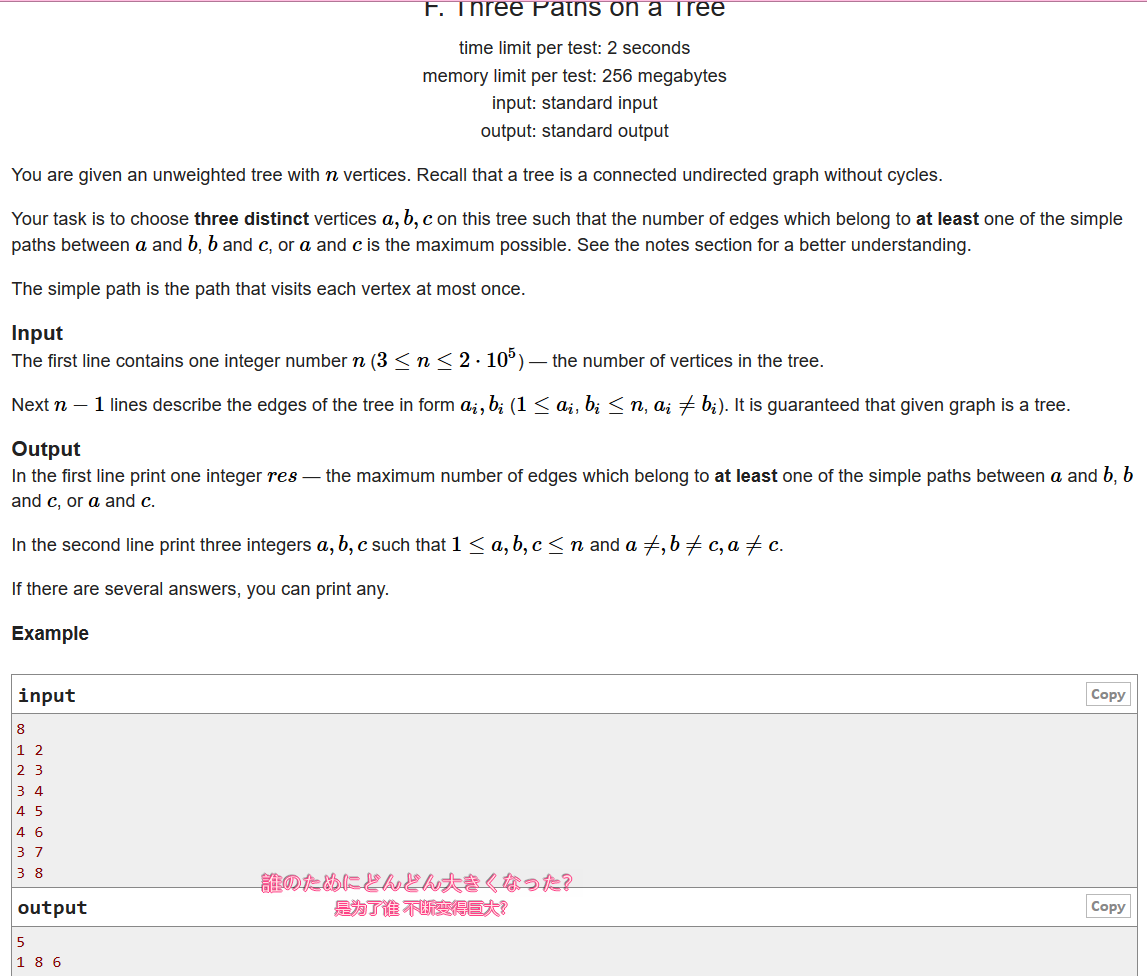
　　两次bfs找出树的直径并处理出端点离树上各叶子节点的距离，在直径上找一点的子树叶子p3，使得dis(p1,p2) + dis(p2,p3) + dis(p1,p3)最大

　　易知上式是路径实长的两倍

 #include <bits/stdc++.h>
 #define dbg(x) cout << #x << "=" << x << endl
 #define eps 1e-8
 #define pi acos(-1.0)

 using namespace std;
 typedef long long LL;

 template<class T>inline void read(T &res)
 {
     char c;T flag=;
     while((c=getchar())<''||c>'')if(c=='-')flag=-;res=c-'';
     while((c=getchar())>=''&&c<='')res=res*+c-'';res*=flag;
 }

 namespace _buff {
     const size_t BUFF =  << ;
     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
     char getc() {
         if (ib == ie) {
             ib = ibuf;
             ie = ibuf + fread(ibuf, , BUFF, stdin);
         }
         return ib == ie ? - : *ib++;
     }
 }

 int qread() {
     using namespace _buff;
     int ret = ;
     bool pos = true;
     char c = getc();
     for (; (c < '' || c > '') && c != '-'; c = getc()) {
         assert(~c);
     }
     if (c == '-') {
         pos = false;
         c = getc();
     }
     for (; c >= '' && c <= ''; c = getc()) {
         ret = (ret << ) + (ret << ) + (c ^ );
     }
     return pos ? ret : -ret;
 }

 const int maxn = 2e5 + ;

 int head[maxn << ], edge[maxn << ], nxt[maxn << ];
 int w[maxn << ];
 int vis[maxn];
 int dis[maxn];

 int n, cnt;

 void BuildGraph(int u, int v, int c) {
     cnt++;
     edge[cnt] = v;
     nxt[cnt] = head[u];
     w[cnt] = c;
     head[u] = cnt;
 }

 int bfs(int x) {
     memset(vis, , sizeof(vis));
     memset(dis, , sizeof(dis));
     int pos = ;
     queue <int> q;
     q.push(x);
     vis[x] = ;
     int u;
     while(!q.empty()) {
         u = q.front();
         //dbg(u);
         q.pop();
         for (int i = head[u]; i; i = nxt[i]) {
             int v = edge[i];
             int d = w[i];
             if(vis[v])
                 continue;
             else {
                 dis[v] = dis[u] + d;
                 vis[u] = ;
                 if(dis[v] > dis[pos]) {
                     pos = v;
                 }
                 q.push(v);
             }
         }
     }
     return pos;
 }

 int d1[maxn], d2[maxn];

 int main()
 {
     read(n);
     int a, b;
     for ( int i = ; i < n; ++i ) {
         read(a);
         read(b);
         BuildGraph(a, b, );
         BuildGraph(b, a, );
     }
     int p1, p2;
     p1 = bfs();
     p2 = bfs(p1);
     for ( int i = ; i <= n; ++i ) {
         d1[i] = dis[i];
     }
     int p3 = bfs(p2);
     for ( int i = ; i <= n; ++i ) {
         d2[i] = dis[i];
     }
     int p4 = ;
     for ( int i = ; i <= n; ++i ) {
         if(d1[i] + d2[i] > d1[p4] + d2[p4] && i != p1 && i != p2) {
             p4 = i;
         }
     }
     int ans = d1[p4]+d2[p4]+d1[p2];
     //dbg(ans);
     printf("%d\n",ans / );
     printf("%d %d %d\n",p1,p2,p4);
     return ;
 }