China Final J - Mr.Panda and TubeMaster

和一般的管道不同

不能类似“无限之环”或者“弯弯国”的建图，因为这两个题都是某些位置必须有，或者必须没有

但是本题可以有的位置随意，不能限制某个位置要么流2，要么流0，（实际上可能流了1过去）

所以建图方式不能一样了。

唯一的好处是：只有四种管道。

横的、竖的，所以考虑拆点

法一：

黑白染色

每个点拆成两个点，横、竖

黑色：横->竖，竖->上下的白点的竖，左右白点的横->横

白色：竖->横，横->到左右黑点的横，上下的黑点->竖

必须的就上下界[1,1]否则[0,1]

也即形如：

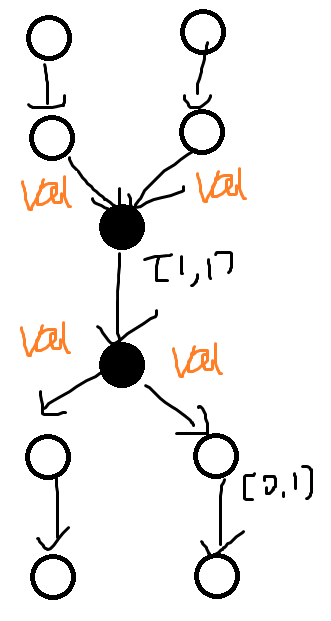
无源汇上下界最大费用可行流。

求出可行流，在第二步增广的时候，费用<0就break掉

直接跑最大费用最大流得到可行流即可。

PS：可能有正环，需要消圈。[学习笔记]费用流

法二：

考虑连成的若干个环

黑白染色

黑色：横向的是出边，纵向的是入边

白色：纵向的是出边，横向的是入边

然后类似“星际竞速”就可以了

如果一个边不需要选择，就入点直接向出点连边。

最大费用最大流。

之所以可以用“星际竞速”建图来做，因为每个边可以有固定的流向。

且一定一个边入，一个边出，最终成环

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);}
template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);}
}
// using namespace Modulo;
namespace Miracle{
const int N=;
const int inf=0x3f3f3f3f;
const int P=*N*N;
int n,m;
struct node{
    int nxt,to;
    int w,c;
}e[*(N*N**)];
int hd[P],cnt=;
int num(int i,int j,int t){
    return t*n*m+(i-)*m+j;
}
void add(int x,int y,int w,int c){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;e[cnt].w=w;e[cnt].c=c;
    hd[x]=cnt;

    e[++cnt].nxt=hd[y];
    e[cnt].to=x;e[cnt].w=;e[cnt].c=-c;
    hd[y]=cnt;
}
int dis[P],vis[P];
int incf[P],pre[P];
bool lim[N][N];
int s,t;
queue<int>q;
int ans,flow;
bool spfa(){
    memset(dis,0xcf,sizeof dis);
    dis[s]=;incf[s]=inf;
    pre[t]=;
    q.push(s);
    while(!q.empty()){
        int x=q.front();q.pop();
        vis[x]=;
        for(reg i=hd[x];i;i=e[i].nxt){
            int y=e[i].to;
            if(e[i].w&&dis[y]<dis[x]+e[i].c){
                dis[y]=dis[x]+e[i].c;
                pre[y]=i;incf[y]=min(incf[x],e[i].w);
                if(!vis[y]){
                    vis[y]=;
                    q.push(y);
                }
            }
        }
    }
    if(!pre[t]) return false;
    return true;
}
void upda(){
    int x=t;
    while(x!=s){
        e[pre[x]].w-=incf[t];
        e[pre[x]^].w+=incf[t];
        x=e[pre[x]^].to;
    }
    ans+=dis[t]*incf[t];
    flow+=incf[t];
}
void clear(){
    memset(hd,,sizeof hd);
    cnt=;
    ans=;flow=;
    s=;t=;
    memset(lim,,sizeof lim);
}
int main(){
    int T;
    rd(T);
    for(reg o=;o<=T;++o){
        rd(n);rd(m);
        clear();
        s=;t=num(n,m,)+;
        int v;
        for(reg i=;i<=n;++i){
            for(reg j=;j<m;++j){
                rd(v);
                if((i+j)&){//white
                    add(num(i,j+,),num(i,j,),,v);
                }else{//black
                    add(num(i,j,),num(i,j+,),,v);
                }
            }
        }
        for(reg i=;i<n;++i){
            for(reg j=;j<=m;++j){
                rd(v);
                if((i+j)&){//white
                    add(num(i,j,),num(i+,j,),,v);
                }else{
                    add(num(i+,j,),num(i,j,),,v);
                }
            }
        }
        int k;
        rd(k);
        int x,y;
        for(reg i=;i<=k;++i){
            rd(x);rd(y);
            lim[x][y]=;
        }
        for(reg i=;i<=n;++i){
            for(reg j=;j<=m;++j){
                add(s,num(i,j,),,);
                add(num(i,j,),t,,);
                if(!lim[i][j]) add(num(i,j,),num(i,j,),,);
            }
        }
        while(spfa()) upda();
        printf("Case #%d: ",o);
        if(flow==n*m){
            printf("%d\n",ans);
        }else{
            printf("Impossible\n");
        }
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

其实两个方法有点类似

都是相当于黑白染色，然后给边定向

法一，通过循环流直接就是环

法二，“星际竞速”图，可以拼成环