Levenshtein distance 编辑距离算法

这几天再看 virtrual-dom，关于两个列表的对比，讲到了 Levenshtein distance 距离，周末抽空做一下总结。

Levenshtein Distance 介绍

在信息理论和计算机科学中，Levenshtein 距离是用于测量两个序列之间的差异量（即编辑距离）的度量。两个字符串之间的 Levenshtein 距离定义为将一个字符串转换为另一个字符串所需的最小编辑数，允许的编辑操作是单个字符的插入，删除或替换。

例子

‘kitten’和’sitten’之间的 Levenshtein 距离是 3，因为一下三个编辑将一个更改为另一个，并且没有办法用少于三个编辑来执行操作。

1. k itten sitten => 用’s’代替’k’
2. sitt e n sitt i => 用’i’代替’e’
3. sittin sittin g 在结尾插入’g’

Levenshtein Distance (编辑距离) 算法详解

为了得到编辑距离，我们用 beauty 和 batyu 为例：

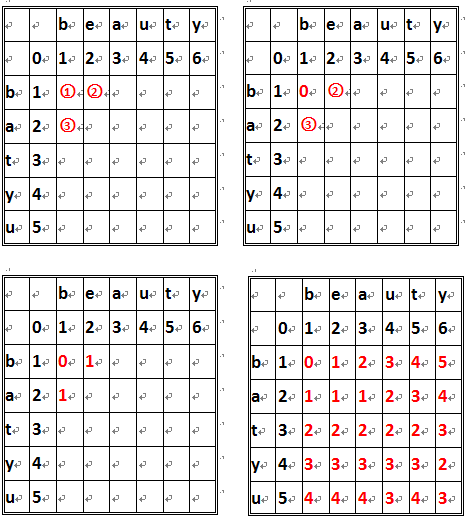
图示如 ① 单元位置是两个单词的第一个字符 [b] 比较得到的值，其的值有它的上方的值 (1)、它左方的值 (1) 和它左上角的值 (0) 来决定。当单元格所在的行和列所对应的字符相等时，单元格的值为左上方的值。

否则，单元格左上角的值与其上方和左方的值进行比较，它们之间的最小值 + 1 即是单元格的值。

图中 ① 的值由于单元格行和列相等，所以取左上角值 0。

图中 ② 的值由于单元格行列不相等，(1, 2, 0) 取最小为 0， 结果 + 1， 所以 ② 值为 1。

图示 ③ 的值由于单元格行列不相等，(1, 0, 2) 取最小 0， 结果 + 1， 所以 ③ 值为 1。

算法证明

这个算法计算的是将 s [1…i] 转换为 t [1…j]（例如将 beauty 转换为 batyu）所需最少的操作数（也就是所谓的编辑距离），这个操作数被保存在 d [i,j]（d 代表的就是上图所示的二维数组）中。

• 在第一行与第一列肯定是正确的，这也很好理解，例如我们将 beauty 转换为空字符串，我们需要进行的操作数为 beauty 的长度（所进行的操作为将 beauty 所有的字符丢弃）。
• 我们对字符的可能操作有三种：
• 将 s [1…n] 转换为 t [1…m] 当然需要将所有的 s 转换为所有的 t，所以，d [n,m]（表格的右下角）就是我们所需的结果。
• 如果我们可以使用 k 个操作数把 s [1…i] 转换为 t [1…j-1]，我们只需要把 t [j] 加在最后面就能将 s [1…i] 转换为 t [1…j]，操作数为 k+1
• 如果我们可以使用 k 个操作数把 s [1…i-1] 转换为 t [1…j]，我们只需要把 s [i] 从最后删除就可以完成转换，操作数为 k+1
• 如果我们可以使用 k 个操作数把 s [1…i-1] 转换为 t [1…j-1]，我们只需要在需要的情况下（s [i] != t [j]）把 s [i] 替换为 t [j]，所需的操作数为 k+cost（cost 代表是否需要转换，如果 s [i]==t [j]，则 cost 为 0，否则为 1）。

可能的改进

• 现在的算法复杂度为 O (m*n)，可以将其改进为 O (m)。因为这个算法只需要上一行和当前行被存储下来就可以了。
• 如果需要重现转换步骤，我们可以把每一步的位置和所进行的操作保存下来，进行重现。
• 如果我们只需要比较转换步骤是否小于一个特定常数 k，那么只计算高宽宽为 2k+1 的矩形就可以了，这样的话，算法复杂度可简化为 O (kl)，l 代表参加对比的最短 string 的长度。
• 我们可以对三种操作（添加，删除，替换）给予不同的权值（当前算法均假设为 1，我们可以设添加为 1，删除为 0，替换为 2 之类的），来细化我们的对比。
• 如果我们将第一行的所有 cell 初始化为 0，则此算法可以用作模糊字符查询。我们可以得到最匹配此字符串的字符串的最后一个字符的位置（index number），如果我们需要此字符串的起始位置，我们则需要存储各个操作的步骤，然后通过算法计算出字符串的起始位置。
• 这个算法不支持并行计算，在处理超大字符串的时候会无法利用到并行计算的好处。但我们也可以并行的计算 cost values（两个相同位置的字符是否相等），然后通过此算法来进行整体计算。
• 如果只检查对角线而不是检查整行，并且使用延迟验证（lazy evaluation），此算法的时间复杂度可优化为 O (m (1+d))（d 代表结果）。这在两个字符串非常相似的情况下可以使对比速度速度大为增加。

字符串比较代码

这一部分的代码，参考了 https://rosettacode.org/wiki/Levenshtein_distance#ES5

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

const ld = (a, b) => { let t = [], u, i, j, m = a.length, n = b.length; if (!m) return b; if (!n) return a; for (j = 0; j <= m; j++) { t[j] = j; } console.log(t); for (i = 1; i <= n; i++) { for (u = [i], j = 1; j <= m; j++) { u[j] = a[j - 1] === b[i - 1] ? t[j - 1] : Math.min(t[j - 1], t[j], u[j - 1]) + 1 // Levenshtein Distance 算法核心比较部分。 } t = u; console.log(t); } return u[m]; } [['beauty', 'batyu', 3], ].forEach(function (v) { var a = v[0], b = v[1], t = v[2], d = ld(a, b); if (d !== t) { console.log('levenstein("' + a + '","' + b + '") was ' + d + ' should be ' + t); } }); // 打印出来 [ 0, 1, 2, 3, 4, 5, 6 ] [ 1, 0, 1, 2, 3, 4, 5 ] [ 2, 1, 1, 1, 2, 3, 4 ] [ 3, 2, 2, 2, 2, 2, 3 ] [ 4, 3, 3, 3, 3, 3, 2 ] [ 5, 4, 4, 4, 3, 4, 3 ]

还原字符串

上面总结了传统的计算字符串之间的差距，那么当我们怎么能在计算的过程中，记录需要转换的步骤，并且进行还原呢。

这里我们需要对比较的每一位的步骤有一个了解。

为了得到编辑距离，我们用 beauty 和 batyu 为例：
从上面一节的图中可以看到，'beauty' 转换为 '' ，对一个的第一行的 [1，2，3，4，5，6]，每一个步骤都相对与上一个元素新建一个元素，同理 '' 转换为 'batyu'，每一个值都是相对一上一个元素的删除步骤。

那么对角线也显而易见就是先相对于替换操作。那么我们现在需要做的就是，记录下相对应的索引和元素以及需要进行的操作，并将其保存为一个对象，每次新增的对象用数组来保存就可以了。

1 2 3 4 5 6 7 8 9 10 11 12 13 14

const actionType = { TYPE_REPLACE: 'TYPE_REPLACE', TYPE_NEW: 'TYPE_NEW', TYPE_DELETE: 'TYPE_DELETE' } // 生成对象的方法 const patchObj = (index, type, item = '') => { return { index, type, item } }

下面是 compare 方法：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

/** * * @param { array } r 替换操作 replace * @param { array } n 新建操作 new * @param { array } d 删除操作 delete * @param { number } i 需要转换元素的 index * @param { number } j 需要删除元素的 index * @param { string } b 比较字符串 */ const compare = (r, n, d, i, j, b) => { const min = Math.min(r.length, n.length, d.length); switch (min) { case r.length: return [...r, patchObj(i, actionType.TYPE_REPLACE, b[i])]; case n.length: return [...n, patchObj(i, actionType.TYPE_NEW, b[i])]; case d.length: return [...d, patchObj(j, actionType.TYPE_DELETE)]; } }

上面需要注意的是，我们一组保存了多个数组对象，不要对原数组进行操作，每一次操作我们都需要拷贝一个新的数组对象。

具体的的 diff 代码参考 diff 代码

得到了，patches 对象，剩下的我们就需要 patch 了

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

const patch = (a, diffs) => { let aList = a.split(''); let delCount = 0; // 删除之后，后续的index计算需要加上之前删除的数量 diffs.forEach((diff) => { switch (diff.type) { case actionType.TYPE_DELETE: aList.splice(diff.index - delCount, 1); delCount++ break; case actionType.TYPE_NEW: aList.splice(diff.index, 0, diff.item); break; case actionType.TYPE_REPLACE: aList.splice(diff.index, 1, diff.item); break; default: break; } }) // console.log(aList.join('')) return aList.join('') }

具体代码参考代码地址

参考资料

• http://www.cnblogs.com/zhoug2020/p/4224866.html
• https://rosettacode.org/wiki/Levenshtein_distance#ES5