可持久化线段树（主席树）——静态区间第k大

主席树基本操作：静态区间第k大

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+,MAXN=2e5+,SIZE=MAXN*;
int N,M,K;
int tmp[MAXN],A[MAXN],rt[MAXN],order[MAXN];
int sz,lson[SIZE],rson[SIZE],sum[SIZE];
int init(int l,int r){
    int cur=++sz;
    if(l<r){
        int mid=(l+r)>>;
        lson[cur]=init(l,mid);
        rson[cur]=init(mid+,r);
    }
    return cur;
}
int modify(int pre,int l,int r,int x){
    int cur=++sz;
    lson[cur]=lson[pre];
    rson[cur]=rson[pre];
    sum[cur]=sum[pre]+;
    int mid=(l+r)>>;
    if(l<r){
        if(x<=mid)
            lson[cur]=modify(lson[pre],l,mid,x);
        else
            rson[cur]=modify(rson[pre],mid+,r,x);
    }
    return cur;
}
int query(int x,int y,int l,int r,int k){
    if(l==r)
        return l;
    int ii=sum[lson[y]]-sum[lson[x]],mid=(l+r)>>;
    if(ii>=k){
        return query(lson[x],lson[y],l,mid,k);
    }else{
        return query(rson[x],rson[y],mid+,r,k-ii);
    }
}
int main(){
    scanf("%d%d",&N,&K);
    for(int i=;i<=N;i++){
        scanf("%d",tmp+i);
        A[i]=tmp[i];
    }
    sort(A+,A+N+);
    int M=unique(A+,A+N+)-A-;
    rt[]=init(,M);
    for(int i=;i<=N;i++){
        order[i]=lower_bound(A+,A+M+,tmp[i])-A;
        rt[i]=modify(rt[i-],,M,order[i]);
    }
    while(K--){
        int ii,jj,kk;
        scanf("%d%d%d",&ii,&jj,&kk);
        printf("%d\n",A[query(rt[ii-],rt[jj],,M,kk)]);
    }
    return ;
}

模板代码

题面：给一个长为n的序列，m次询问，每次询问[l, r]内第k大的数是几。 n <= 100000, m <= 5000

主席树实现：参考自bestFy （作者：bestFy，来源：CSDN ）

首先我们要将所有数字离散化。主席树相当于是在每个位置维护了一个线段树，线段树的节点是一个区间[x, y]，这里的x和y都是离散后数的编号。

当然如果真的在每个位置建一棵线段树，空间肯定爆炸，不过我们先不管这个问题。

主席树节点中维护的值，是1~i之间这个区间内出现了数的次数。然后当我们查询的时候，就是利用到了前缀和的思想

区间[x,y]中每个数字出现的次数即为第y棵线段树中的值-第x-1棵线段树中的值

然后我们来模拟一下一组数据吧。

首先建树。

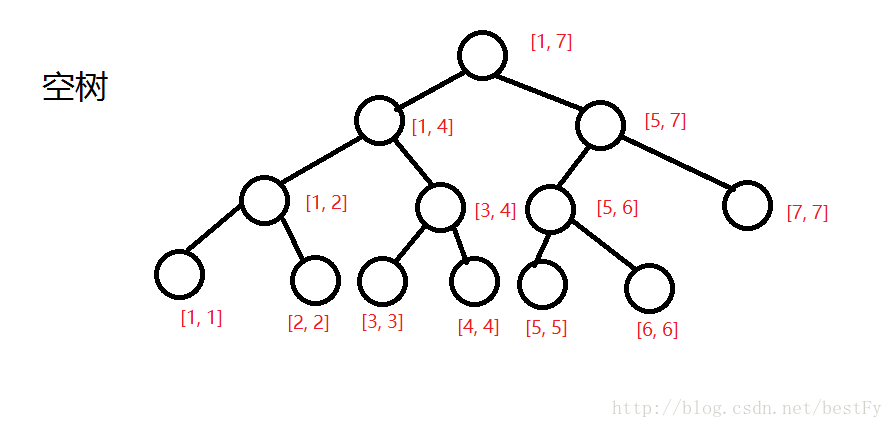
然后我们逐一插入数字。

将每个数字的大小（即离散化后的编号）插入到它的位子上，然后并把所有包括它的区间的sum都++。

  

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

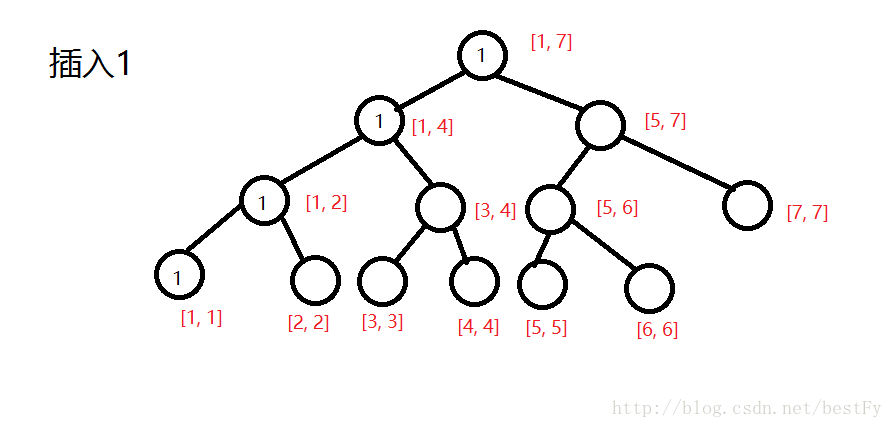
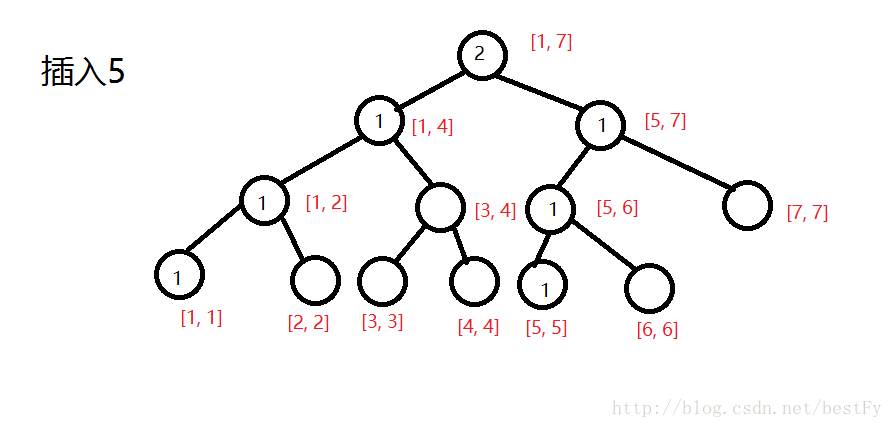
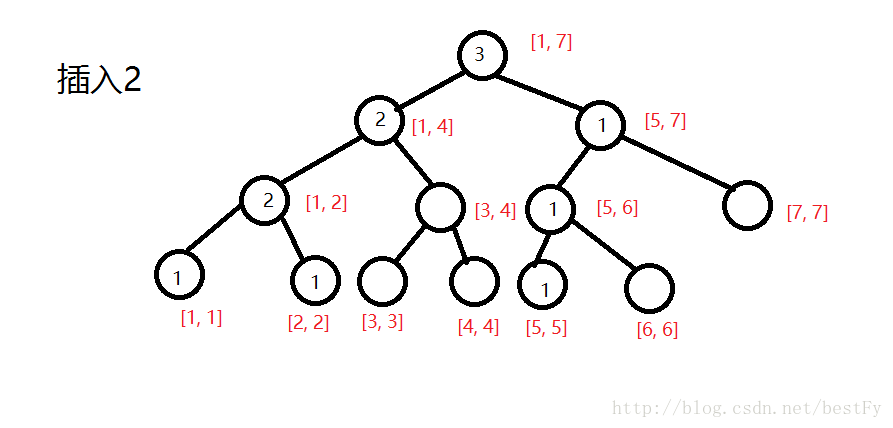
直到把所有数字插入以后，情况是这样的。

那么建树的具体过程大致如上

接下来我们考虑查询。

要查询[2, 5]中第3大的数我们首先把第1棵线段树和第5棵拿出来。

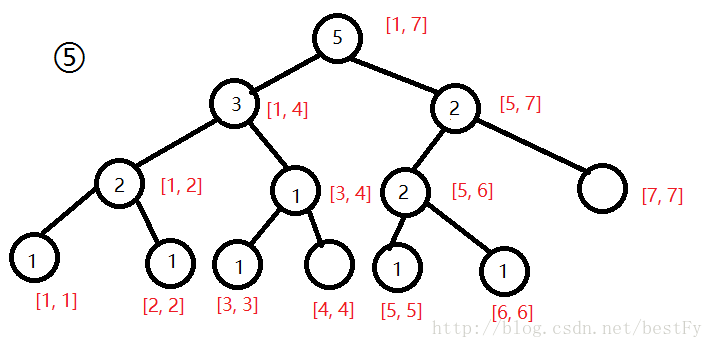
然后我们发现，将对应节点的数相减，刚刚好就是[2, 5]内某个范围内的数的个数。比如[1, 4]这个节点相减是2，就说明[2. 5]内有2个数是在1~4范围内（就是2, 3）。

所以对于一个区间[l, r]，我们可以每次算出在[l, mid]范围内的数，如果数量>=k（k就是第k大），就往左子树走，否则就往右子树走。

代码实现：

我们用动态开点线段树，定义一些变量

int N：数字总数,M：离散化后数字总数,K：查询数量;
int tmp[MAXN]：记录数值大小,A[MAXN]：排序的数值,rt[MAXN]：每一个节点的线段树的根节点,order[MAXN]：每一个数字的排名;
int sz：线段树节点总数,lson[SIZE]：左儿子下标,rson[SIZE]：右儿子下标,sum[SIZE]：统计和;

建树：先建一棵空的权值线段树，所有点的值都是0

int init(int l,int r){
    int cur=++sz;
    if(l<r){
        int mid=(l+r)>>;
        lson[cur]=init(l,mid);
        rson[cur]=init(mid+,r);
    }
    return cur;
}

插入：

我们将N个数离散化，按照排名统计到N棵线段树上

for(int i=;i<=N;i++){
    scanf("%d",tmp+i);
    A[i]=tmp[i];
}
sort(A+,A+N+);
int M=unique(A+,A+N+)-A-;
rt[]=init(,M);
for(int i=;i<=N;i++){
    order[i]=lower_bound(A+,A+M+,tmp[i])-A;
    rt[i]=modify(rt[i-],,M,order[i]);
}

每次建立一棵新的线段树，但如果建一棵全新的，空间和时间都会爆炸

因为我们更新一个节点的值，只有一条logM的链上的值会改变，所以没有更改的节点都可以使用上一棵树的

每一次只要按照线段树的方式遍历，需要加的儿子则新建，否则将儿子指向上一棵树的儿子

int modify(int pre,int l,int r,int x){
    int cur=++sz;
    lson[cur]=lson[pre];
    rson[cur]=rson[pre];
    sum[cur]=sum[pre]+;
    int mid=(l+r)>>;
    if(l<r){
        if(x<=mid)
            lson[cur]=modify(lson[pre],l,mid,x);
        else
            rson[cur]=modify(rson[pre],mid+,r,x);
    }
    return cur;
}

查询：

因为第i棵线段树每个节点的值为区间[1,i]上每个数字出现的数字，所以第y棵树的每个节点的值-第x-1棵树的每个节点的值即为区间[x,y]上每一个数字出现的次数

while(K--){
    int ii,jj,kk;
    scanf("%d%d%d",&ii,&jj,&kk);
    printf("%d\n",A[query(rt[ii-],rt[jj],,M,kk)]);
}

每一次在权值线段树上查询区间第k大：

int query(int x,int y,int l,int r,int k){
    if(l==r)
        return l;
    int ii=sum[lson[y]]-sum[lson[x]],mid=(l+r)>>;
    if(ii>=k){
        return query(lson[x],lson[y],l,mid,k);
    }else{
        return query(rson[x],rson[y],mid+,r,k-ii);
    }
}

最终代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF=1e9+,MAXN=2e5+,SIZE=MAXN*;
 int N,M,K;
 int tmp[MAXN],A[MAXN],rt[MAXN],order[MAXN];
 int sz,lson[SIZE],rson[SIZE],sum[SIZE];
 int init(int l,int r){
     int cur=++sz;
     if(l<r){
         int mid=(l+r)>>;
         lson[cur]=init(l,mid);
         rson[cur]=init(mid+,r);
     }
     return cur;
 }
 int modify(int pre,int l,int r,int x){
     int cur=++sz;
     lson[cur]=lson[pre];
     rson[cur]=rson[pre];
     sum[cur]=sum[pre]+;
     int mid=(l+r)>>;
     if(l<r){
         if(x<=mid)
             lson[cur]=modify(lson[pre],l,mid,x);
         else
             rson[cur]=modify(rson[pre],mid+,r,x);
     }
     return cur;
 }
 int query(int x,int y,int l,int r,int k){
     if(l==r)
         return l;
     int ii=sum[lson[y]]-sum[lson[x]],mid=(l+r)>>;
     if(ii>=k){
         return query(lson[x],lson[y],l,mid,k);
     }else{
         return query(rson[x],rson[y],mid+,r,k-ii);
     }
 }
 int main(){
     scanf("%d%d",&N,&K);
     for(int i=;i<=N;i++){
         scanf("%d",tmp+i);
         A[i]=tmp[i];
     }
     sort(A+,A+N+);
     int M=unique(A+,A+N+)-A-;
     rt[]=init(,M);
     for(int i=;i<=N;i++){
         order[i]=lower_bound(A+,A+M+,tmp[i])-A;
         rt[i]=modify(rt[i-],,M,order[i]);
     }
     while(K--){
         int ii,jj,kk;
         scanf("%d%d%d",&ii,&jj,&kk);
         printf("%d\n",A[query(rt[ii-],rt[jj],,M,kk)]);
     }
     return ;
 }