leetcode-分治

题目169：

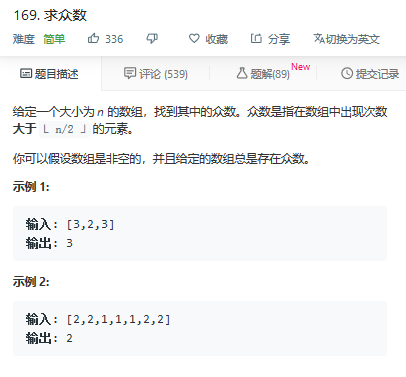
分治：O(nlgn)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        def majorE(lo,hi):
            if lo == hi:
                return nums[lo]
            mid = (lo + hi)//2
            left = majorE(lo,mid)
            right = majorE(mid+1,hi)
            if left == right:
                return left
            else:
                left_count = sum(1 for i in range(lo,hi+1) if left==nums[i])
                right_count = sum(1 for i in range(lo,hi+1) if right==nums[i])
                return left if left_count>right_count else right
        res = majorE(0,len(nums)-1)
        return res

题241：

分治：

class Solution:
    def diffWaysToCompute(self, input):
        if input.isdigit():
            return [int(input)]
        elif not input:
            return []
        tem = []
        for k in range(len(input)):
            if input[k] == '+':
                tem.extend([i + j for i in self.diffWaysToCompute(input[:k]) for j in self.diffWaysToCompute(input[k + 1:])])
            elif input[k] == '-':
                tem.extend([i - j for i in self.diffWaysToCompute(input[:k]) for j in self.diffWaysToCompute(input[k + 1:])])
            elif input[k] == '*':
                tem.extend([i * j for i in self.diffWaysToCompute(input[:k]) for j in self.diffWaysToCompute(input[k + 1:])])
        return te

题932：*

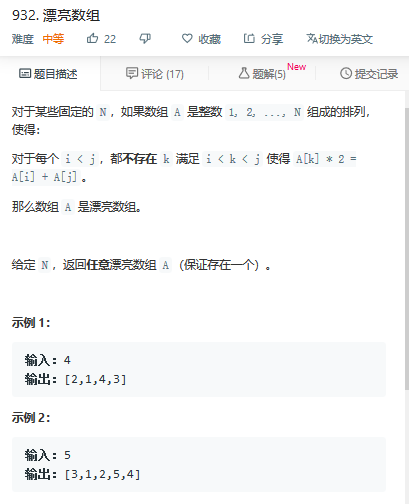
分治：

class Solution:
    def beautifulArray(self, N):
        memo = {1: [1]}
        def f(N):
            if N not in memo:
                odds = f((N+1)/2)
                evens = f(N/2)
                memo[N] = [2*x-1 for x in odds] + [2*x for x in evens]
            return memo[N]
        return f(N)

题973：

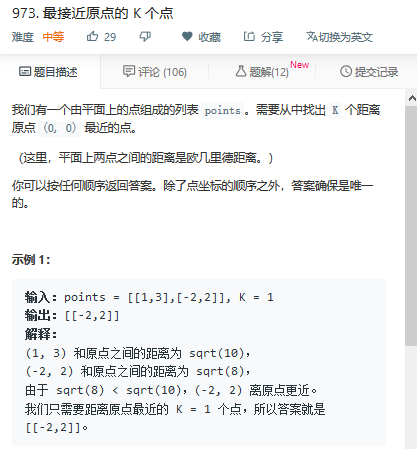
可参考：题215

分治：

class Solution:
    def kClosest(self, points: List[List[int]], K: int) -> List[List[int]]:
        # 计算欧几里得距离
        distance = lambda i: points[i][0] ** 2 + points[i][1] ** 2

        def work(i, j, K):
            if i > j:
                return
            # 记录初始值
            oi, oj = i, j
            # 取最左边为哨兵值
            pivot = distance(oi)
            while i != j:
                while i < j and distance(j) >= pivot:
                    j -= 1
                while i < j and distance(i) <= pivot:
                    i += 1
                if i < j:
                    # 交换值
                    points[i], points[j] = points[j], points[i] 

            # 交换哨兵
            points[i], points[oi] = points[oi], points[i]

            # 递归
            if K <= i - oi + 1:
                # 左半边排序
                work(oi, i - 1, K)
            else:
                # 右半边排序
                work(i + 1, oj, K - (i - oi + 1))

        work(0, len(points) - 1, K)
        return points[:K]

题：23

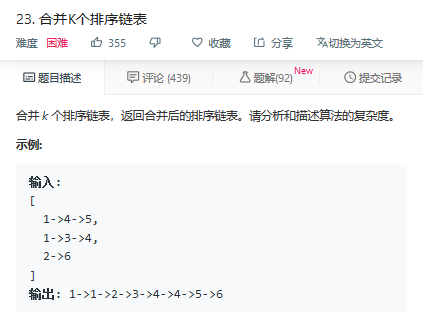
方法一：分治

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if not lists:return
        return self.merge(lists,0,len(lists)-1)
    def merge2lists(self,l1,l2):
        if not l1:return l2
        if not l2:return l1
        if l1.val<l2.val:
            l1.next = self.merge2lists(l1.next,l2)
            return l1
        else:
            l2.next = self.merge2lists(l1,l2.next)
            return l2
    def merge(self,lists,left,right):
        if left==right:
            return lists[left]
        mid = (right-left)//2 + left
        l1 = self.merge(lists,left,mid)
        l2 = self.merge(lists,mid+1,right)
        return self.merge2lists(l1,l2)

题目218：

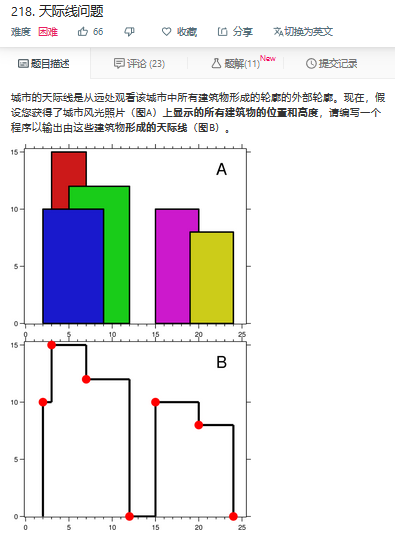
方法一：分治 O(nlogn)

class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        if not buildings:return []
        if len(buildings)==1:
            return [[buildings[0][0], buildings[0][2]], [buildings[0][1], 0]]
        mid = len(buildings)//2
        left = self.getSkyline(buildings[:mid])
        right = self.getSkyline(buildings[mid:])
        return self.merge(left,right)

    def merge(self,left,right):
        l,r = 0,0
        lh,rh = 0,0
        res = []
        while l<len(left) and r<len(right):
            if left[l][0]<right[r][0]:
                cp = [left[l][0], max(left[l][1], rh)]
                lh = left[l][1]
                l += 1
            elif left[l][0] > right[r][0]:
                cp = [right[r][0], max(right[r][1], lh)]
                rh = right[r][1]
                r += 1
            # 相等情况
            else:
                cp = [left[l][0], max(left[l][1], right[r][1])]
                lh = left[l][1]
                rh = right[r][1]
                l += 1
                r += 1
            if len(res)==0 or res[-1][1]!=cp[1]:
                res.append(cp)
        res.extend(left[l:] or right[r:])
        return res