路径规划算法 - 求解最短路径 - Dijkstra(迪杰斯特拉)算法

Dijkstra(迪杰斯特拉)算法的思想是广度优先搜索（BFS） 贪心策略。

是从一个顶点到其余各顶点的最短路径算法，节点边是不各自不同的权重，但都必须是正数

如果是负数，则需要 Bellman-Ford 算法

如果想求任意两点之间的距离，就需要用 Floyd 算法

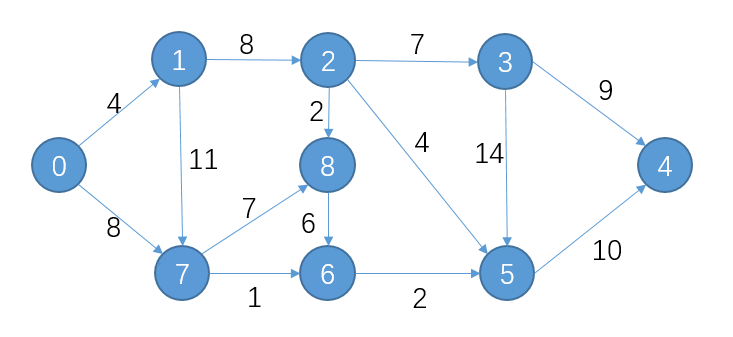
求节点0 -> 4 的最短路径

• 每次从未标记的节点中选择距离出发点最近的节点，标记，收录到最优路径集合中
• 计算刚加入节点A的邻近节点B的距离（不包括标记的节点），若（节点A的距离 + 节点A到节点B的边长）< 节点B的距离，就更新节点B的距离和前序节点

初始状态

节点	0	1	2	3	4	5	6	7	8	备注
最优节点										每一步，找出未标记的节点中，最短的距离，标记为最优节点
出发节点	∞	∞	∞	∞	∞	∞	∞	∞	∞	当前节点，到每个节点的距离，刚开始，所有的节点都认为是 ∞ 无穷大
前序点										为了记录最短路径，需要记录每个节点的前序节点

从0出发

节点	0	1	2	3	4	5	6	7	8
最优节点	️
0 出发	0	∞	∞	∞	∞	∞	∞	∞	∞
前序点

首先，节点0的距离是0，所有节点中距离最短的是它自己，0为最优路径中的节点

更新0邻近节点1、7

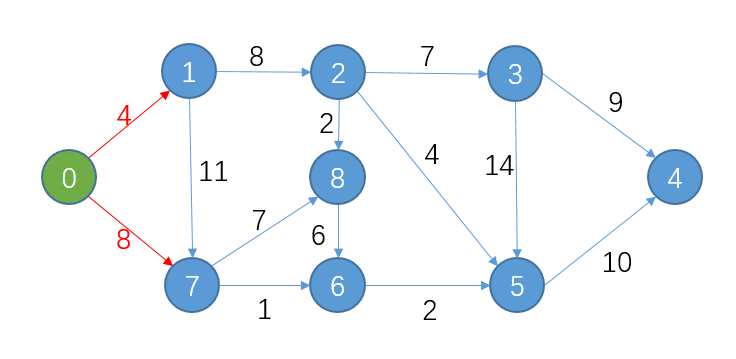
从0点出发，到 相邻的节点 1、7

0->1 = 4 , 节点 1 此时为 ∞，因此 节点 1 的 距离 标为 4，前序节点为 0

0->7 = 8 , 节点 7 此时为 ∞，因此 节点 7 的 距离 标为 8，前序节点为 0

从未标记最优节点（1~8）中，找距离出发点最小的节点 => 1

节点	0	1	2	3	4	5	6	7	8
最优节点		️
0 出发	0	4	∞	∞	∞	∞	∞	8	∞
前序点		0						0

更新1邻近节点2、7

上一次的最优节点是 1

从0点出发，到 节点 1 相邻的节点 2、7

0->1->2 = 4 + 8 = 12 , 节点 2 此时为 ∞，因此 节点 2 的 距离 标为 12，前序节点为 1

0->1->7 = 4 + 11 = 15 , 节点 7 已有值 8，8<15，因此 节点7 的 距离、前序节点保持不变

从未标记最优节点（2~8）中，找距离出发点最小的节点 => 7

节点	0	1	2	3	4	5	6	7	8
最优节点								️
0 出发	0	4	12	∞	∞	∞	∞	8	∞
前序点		0	1					0

更新7邻近节点 8、6

上一次的最优节点是 7

从0点出发，到 节点 7 相邻的节点 8、6

0->7->8 = 8 + 7 = 15 , 节点 8 此时为 ∞，因此 节点 8 的 距离 标为 15，前序节点为 7

0->7->6 = 8 + 1 = 9 , 节点 6 此时为 ∞，因此 节点 6 的 距离 标为 9，前序节点为 7

从未标记最优节点（2~6、8）中，找距离出发点最小的节点 => 6

节点	0	1	2	3	4	5	6	7	8
最优节点							️
0 出发	0	4	12	∞	∞	∞	9	8	15
前序点		0	1				7	0	7

更新6邻近节点 8、5

上一次的最优节点是 6

从0点出发，到 节点 6 相邻的节点 8、5

0->7->6->8 = 8 + 1 + 6 = 15 , 节点 8 已有值 15，15=15，因此 节点 8 的 距离、前序节点保持不变

0->7->6->5 = 8 + 1 + 2 = 11 , 节点 5 此时为 ∞，因此 节点 5 的 距离 标为 11，前序节点为 6

从未标记最优节点（2~5、8）中，找距离出发点最小的节点 => 5

节点	0	1	2	3	4	5	6	7	8
最优节点						️
0 出发	0	4	12	∞	∞	11	9	8	15
前序点		0	1			6	7	0	7

更新5邻近节点 2、3、4

上一次的最优节点是 5

从0点出发，到 节点 5 相邻的节点 2、3、4

0->7->6->5->2 = 8 + 1 + 2 + 4 = 15 , 节点 2 已有值 12，12<15，因此 节点2 的 距离、前序节点保持不变

0->7->6->5->3 = 8 + 1 + 2 + 14 = 25 , 节点 3 此时为 ∞，因此 节点 3 的 距离 标为 25，前序节点为 5

0->7->6->5->4 = 8 + 1 + 2 + 10 = 21 , 节点 4 此时为 ∞，因此 节点 4 的 距离 标为 21，前序节点为 5

从未标记最优节点（2、3、4、8）中，找距离出发点最小的节点 => 2

节点	0	1	2	3	4	5	6	7	8
最优节点			️
0 出发	0	4	12	25	21	11	9	8	15
前序点		0	1	5	5	6	7	0	7

更新2邻近节点 3、8

上一次的最优节点是 2

从0点出发，到 节点 2 相邻的节点 3、5、8，节点5已标记，所以不处理节点5

0->1->2->3 = 4 + 8 + 7 = 19 , 节点 3 已有值 25，25>19，因此 节点 3 的 距离 标为 19，前序节点为 2

0->1->2->8 = 4 + 8 + 2 = 14 , 节点 8 已有值 15，15>14，因此 节点 8 的 距离 标为 14，前序节点为 2

从未标记最优节点（3、4、8）中，找距离出发点最小的节点 => 8

节点	0	1	2	3	4	5	6	7	8
最优节点									️
0 出发	0	4	12	19	21	11	9	8	14
前序点		0	1	2	5	6	7	0	2

更新8邻近节点

上一次的最优节点是 8

8的邻近节点，2、7、6 都已被标记为最优节点，所以不需要处理

从未标记最优节点（3、4）中，找距离出发点最小的节点 => 3

节点	0	1	2	3	4	5	6	7	8
最优节点				️
0 出发	0	4	12	19	21	11	9	8	14
前序点		0	1	2	5	6	7	0	2

更新3邻近节点

上一次的最优节点是 3

最优节点3的邻近节点：2、5、4中 2、5都已被标记为最优节点，处理 4

0->1->2->3->4 = 19 + 9 = 28 , 节点 4 已有值 21，21<28，因此 节点 4 的 距离 、前序节点保持不变

从未标记最优节点（4）中，找距离出发点最小的节点 => 4

节点	0	1	2	3	4	5	6	7	8
最优节点					️
0 出发	0	4	12	19	21	11	9	8	14
前序点		0	1	2	5	6	7	0	2

已时已全部结束

最短距离

从出发点0 到节点 4 的最短距离 = 21

最短路径

反向追溯

4 的前序节点 5，5的前面是 6 ... => 4 -> 5 -> 6 -> 7 -> 0

因此 0 -> 7 -> 6 -> 5 -> 4 是最短路径

https://www.bilibili.com/video/BV1zz4y1m7Nq