线性dp:大盗阿福(打家劫舍)
大盗阿福
- 本题与leetcode198题——打家劫舍的题意一模一样,阅读完本文以后可以尝试以下题目
题目叙述:
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有N家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。作为一向谨慎作案的大盗阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
- 输入的第一行是一个整数T,表示一共有T组数据。
- 接下来的每组数据,第一行是一个整数N,表示一有N家店铺。
- 第二行是N个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。
输出格式
- 对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24
样例解释:
- 对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。对于第二组样例,阿福选择第1和4家店铺行窃获得的现金数量为10+14=24.
动态规划思路分析
- 设我们打劫的店铺数量为
i,获取的价值和为dp,那么dp明显是i的一个函数,那么我们就用dp[i]作为状态变量,dp[i]表示偷前i家店铺所能获取的价值最大值
状态变量以及它的含义
- 由上面分析可知,我们设立
dp[i]作为状态变量,并且dp[i]的含义是偷前i家店铺所能获取收益的最大值.
递推公式
- 我们设
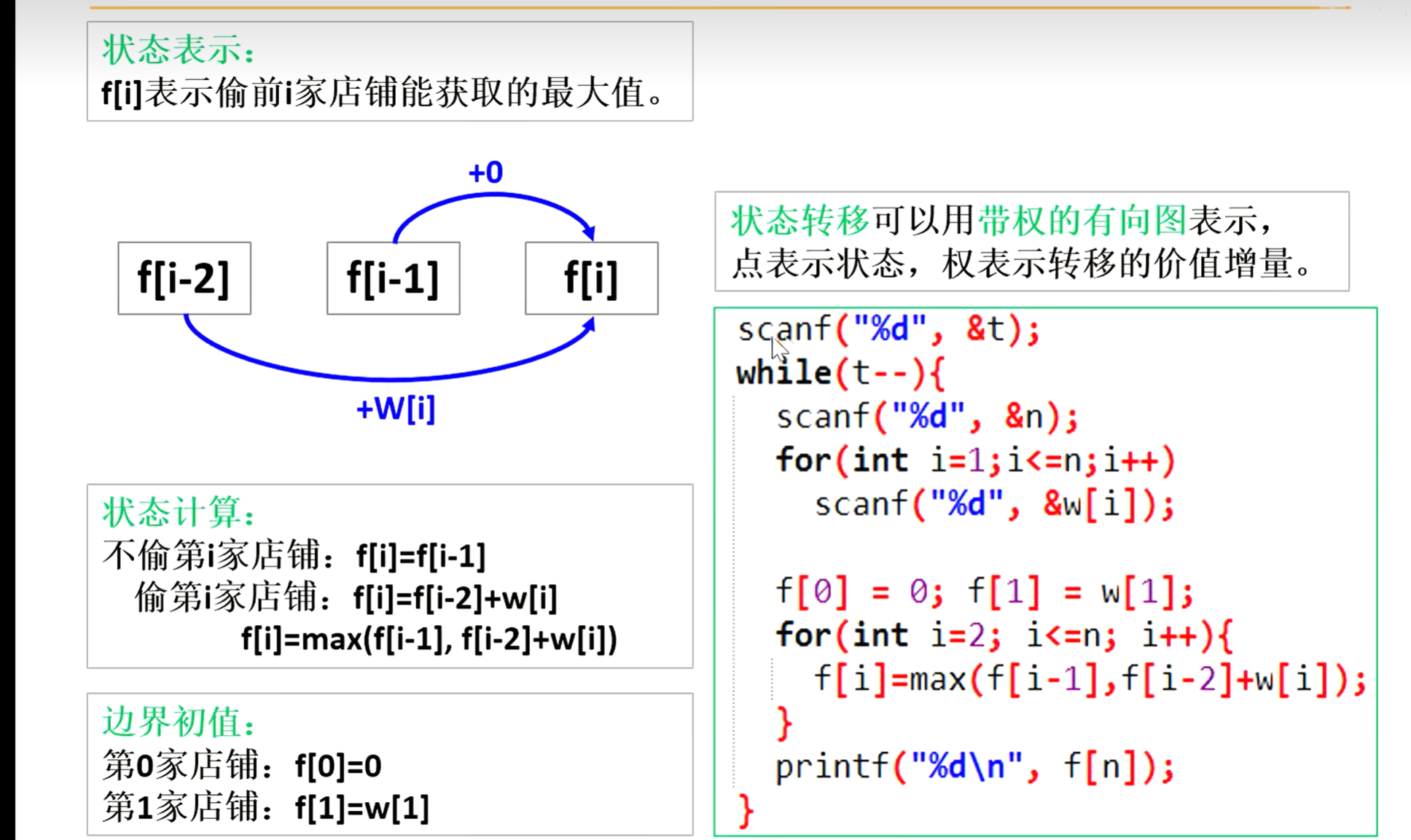
dp[i],在i的这个位置有两种状态:- 1.第i家店铺不偷——
dp[i]=dp[i-1] - 2.第i家店铺偷——
dp[i]=dp[i-2]+w[i],w[i]为第i家店铺的价值
- 1.第i家店铺不偷——
具体细节如下图所示:
遍历顺序:
- 由上面两步分析可知,
dp[i]的状态一定是由前面dp[i-1],dp[i-2],推出来的,所以说遍历顺序一定是从前向后遍历。
如何初始化?
- 我们首先得处理好边界条件:
dp[0]和dp[1]怎么处理? - 偷前0家店铺的最大价值显然是
0,偷前1家店铺的最大价值显然为w[1] - 处理好边界条件以后,我们再从前向后,依据递推公式进行递推就行了
举例验证dp数组
下标:1,2,3,4
w[i]:10,7,6,14
dp[i]:10,10,16,24
- 通过样例2分析可知,我们的dp数组没有分析错。因此我们验证了我们的dp数组的正确性。
优化
我们可以用
dp[i-1]的状态直接推出dp[i]的状态。我们状态表示可以优化成:
f[i][0]表示不偷第i家店铺能获取的最大值f[i][1]表示偷第i家店铺能获取的最大值
那么我们的状态转移方程就可以从
dp[i-1]推出,不偷第i家店铺,那么我们就可以偷第i-1家店铺,也可以不偷,我们选取这两个之中的最大值,如果偷第i家店铺的话,第i-1家店铺我们一定只能选择不偷。- 不偷:
dp[i][0]=max(dp[i-1][0],dp[i-1][1]) - 偷:
dp[i][1]=dp[i-1][0]+w[i]
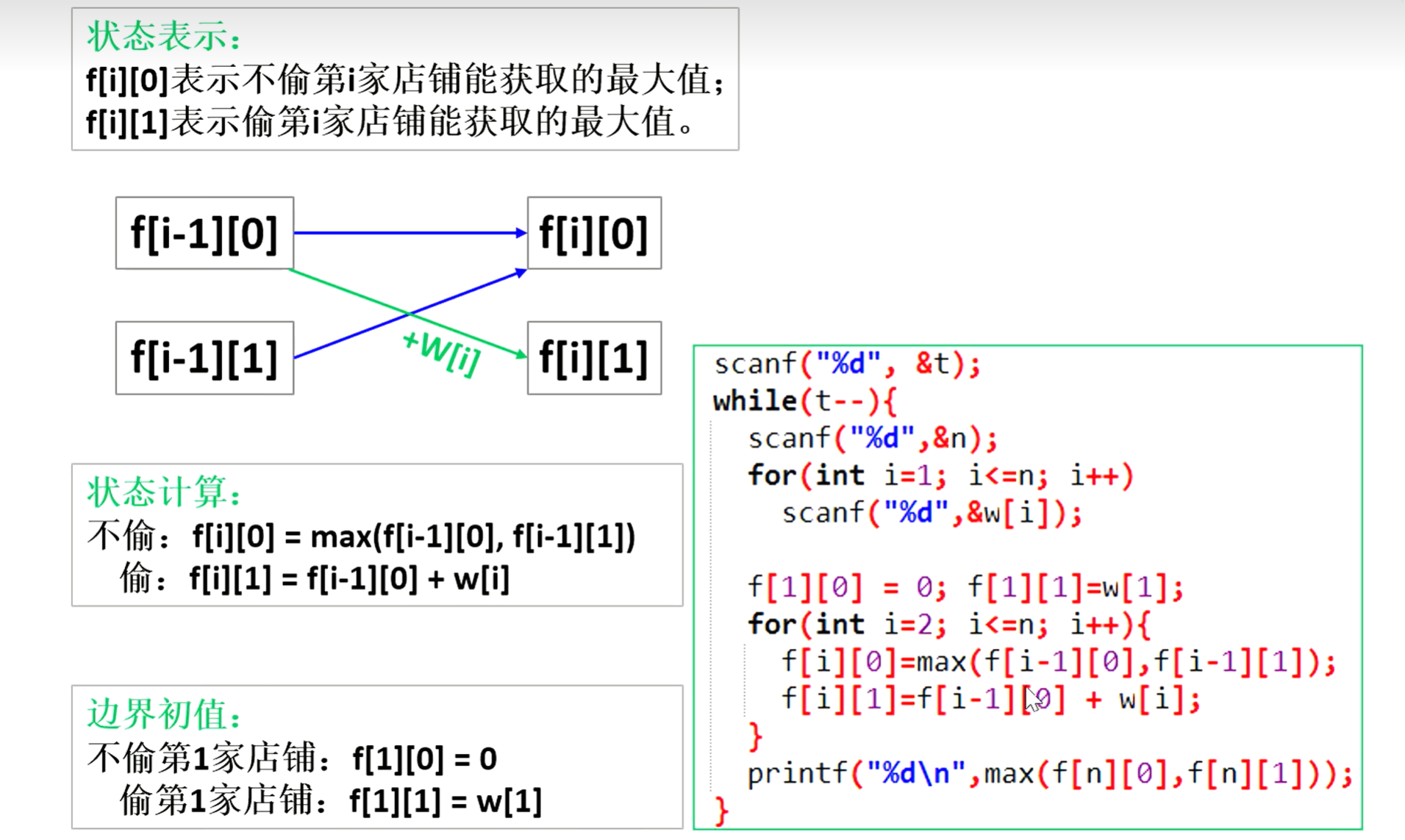
- 不偷:
优化后的边界处理:
- 不偷第1家店铺:
f[i][0]=0 - 偷第1家店铺:
f[i][1]=w[1]
优化后的代码处理:
scanf("%d",&t)
while(t--){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
f[1][0]=0;f[1][1]=w[1];
for(int i=2;i<=n;i++){
f[i][0]=max(f[i-1][0],f[i-1][1]);
f[i][1]=f[i-1][0]+w[i];
}
printf("%d\n",max(f[n][0],f[n][1]));
}
总结:

- 我们上面讲述的两种方法,第一种方法叫做分步转移,第二种方法叫做分类转移,在有些情况下,二者都能使用,而在某些题目当中,只能使用分类转移的方法,我们在以后也会介绍的!希望大家能理解这两种做法。
线性dp:大盗阿福(打家劫舍)的更多相关文章
- [OpenJudge8462][序列DP]大盗阿福
大盗阿福 总时间限制: 1000ms 内存限制: 65536kB [描述] 阿福是一名经验丰富的大盗.趁着月黑风高,阿福打算今晚洗劫一条街上的店铺. 这条街上一共有 N 家店铺,每家店中都有一些现金. ...
- LightOJ1044 Palindrome Partitioning(区间DP+线性DP)
问题问的是最少可以把一个字符串分成几段,使每段都是回文串. 一开始想直接区间DP,dp[i][j]表示子串[i,j]的答案,不过字符串长度1000,100W个状态,一个状态从多个状态转移来的,转移的时 ...
- Codeforces 176B (线性DP+字符串)
题目链接: http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=28214 题目大意:源串有如下变形:每次将串切为两半,位置颠倒形成 ...
- hdu1712 线性dp
//Accepted 400 KB 109 ms //dp线性 //dp[i][j]=max(dp[i-1][k]+a[i][j-k]) //在前i门课上花j天得到的最大分数,等于max(在前i-1门 ...
- 动态规划——线性dp
我们在解决一些线性区间上的最优化问题的时候,往往也能够利用到动态规划的思想,这种问题可以叫做线性dp.在这篇文章中,我们将讨论有关线性dp的一些问题. 在有关线性dp问题中,有着几个比较经典而基础的模 ...
- POJ 2479-Maximum sum(线性dp)
Maximum sum Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 33918 Accepted: 10504 Des ...
- poj 1050 To the Max(线性dp)
题目链接:http://poj.org/problem?id=1050 思路分析: 该题目为经典的最大子矩阵和问题,属于线性dp问题:最大子矩阵为最大连续子段和的推广情况,最大连续子段和为一维问题,而 ...
- nyoj44 子串和 线性DP
线性DP经典题. dp[i]表示以i为结尾最大连续和,状态转移方程dp[i] = max (a[i] , dp[i - 1] + a[i]) AC代码: #include<cstdio> ...
- 『最大M子段和 线性DP』
最大M子段和(51nod 1052) Description N个整数组成的序列a[1],a[2],a[3],-,a[n],将这N个数划分为互不相交的M个子段,并且这M个子段的和是最大的.如果M &g ...
- 『最长等差数列 线性DP』
最长等差数列(51nod 1055) Description N个不同的正整数,找出由这些数组成的最长的等差数列. 例如:1 3 5 6 8 9 10 12 13 14 等差子数列包括(仅包括两项的不 ...
随机推荐
- 半夜被慢查询告警吵醒,limit深度分页的坑
分享是最有效的学习方式. 博客:https://blog.ktdaddy.com/ 故事 梅雨季,闷热的夜,令人窒息,窗外一道道闪电划破漆黑的夜幕,小猫塞着耳机听着恐怖小说,辗转反侧,终于睡意来了,然 ...
- Nuxt3 的生命周期和钩子函数(八)
title: Nuxt3 的生命周期和钩子函数(八) date: 2024/6/30 updated: 2024/6/30 author: cmdragon excerpt: 摘要:本文介绍了Nuxt ...
- Java基础:线程的三种创建方式
一.继承Thread类 定义一个类继承线程类Thread 重写run()方法 创建线程对象 调用线程对象的start()方法创建线程 Thread类的常用API setName(String name ...
- 随机数据下 Sqrt Tree 的平替实现
原理 在随机数据下,把原序列分成 \(\sqrt n\) 个块,维护每个块的前缀后缀最大值,那么,在随机询问下,对于在一个块中的询问,暴力查询. 复杂度 概率 $ n ^ {-\frac{1}{2}} ...
- spring cloud 上云的情况下,Ribbon 客户端负载均衡 与 ALB 服务端负载均衡的选择
在云环境(例如AWS)中,由于云提供商通常提供强大的负载均衡服务(如AWS的ALB),一般不再需要使用Ribbon这种客户端负载均衡方案.云环境中的负载均衡器通常能够提供更高的可靠性.可扩展性和简化的 ...
- 2. 标签上 title 与 alt 属性的区别是什么?
1. alt 是给搜索引擎识别,在图像无法显示时的替代文本2. title 是关于元素的注释信息,主要是给用户解读.3.当鼠标放到文字或是图片上时有 title 文字显示.(因为 IE 不标准)在 I ...
- Oracle 存储过程 捕获异常
1.带参数插入并带返回值,异常信息 CREATE OR REPLACE PROCEDURE test_pro (v_id in int,v_name in varchar2,app_code out ...
- 使用@nuxtjs/sitemap给项目添加sitemap(网站地图)
安装使用步骤参照:此博客内容转载博客地址:https://huangliangbo.com/2097 如何使用?(详细图文) 在项目根目录下使用yarn/npm/cnpm 安装 @nuxtjs/sit ...
- P2918
[USACO08NOV]Buying Hay S 题意描述 约翰的干草库存已经告罄,他打算为奶牛们采购 H(1 \leq H \leq 50000)H(1≤H≤50000) 磅干草. 他知道 N(1 ...
- 机器学习策略篇:详解处理数据不匹配问题(Addressing data mismatch)
处理数据不匹配问题 如果您的训练集来自和开发测试集不同的分布,如果错误分析显示有一个数据不匹配的问题该怎么办?这个问题没有完全系统的解决方案,但可以看看一些可以尝试的事情.如果发现有严重的数据不匹配问 ...