2021-05-26：给定一个char[][] matrix

2021-05-26：给定一个char[][] matrix，也就是char类型的二维数组，再给定一个字符串word，可以从任何一个某个位置出发，可以走上下左右，能不能找到word？char[][] m = {{ ‘a’, ‘b’, ‘z’ }, { ‘c’, ‘d’, ‘o’ }, { ‘f’, ‘e’, ‘o’ }}。设定1：可以走重复路的情况下，返回能不能找到。比如，word = “zoooz”，是可以找到的，z -> o -> o -> o -> z，因为允许走一条路径中已经走过的字符。设定2：不可以走重复路的情况下，返回能不能找到。比如，word = “zoooz”，是不可以找到的，因为允许走一条路径中已经走过的字符不能重复走。

福大大 答案2021-05-26：

自然智慧即可。
递归。对于不可重复的情况，进入递归，走过的位置需要标记为0；退出递归，走过的位置需要恢复成原来的值。

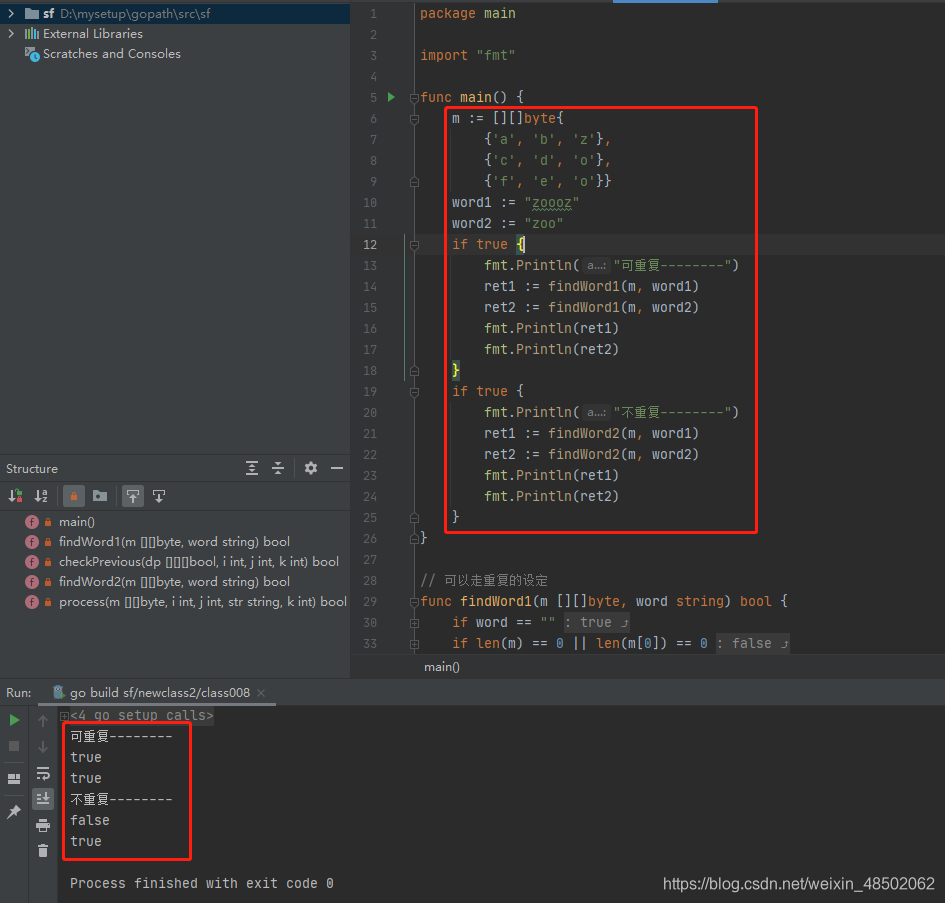
代码用golang编写。代码如下：

package main

import "fmt"

func main() {
    m := [][]byte{
        {'a', 'b', 'z'},
        {'c', 'd', 'o'},
        {'f', 'e', 'o'}}
    word1 := "zoooz"
    word2 := "zoo"
    if true {
        fmt.Println("可重复--------")
        ret1 := findWord1(m, word1)
        ret2 := findWord1(m, word2)
        fmt.Println(ret1)
        fmt.Println(ret2)
    }
    if true {
        fmt.Println("不重复--------")
        ret1 := findWord2(m, word1)
        ret2 := findWord2(m, word2)
        fmt.Println(ret1)
        fmt.Println(ret2)
    }
}

// 可以走重复的设定
func findWord1(m [][]byte, word string) bool {
    if word == "" {
        return true
    }
    if len(m) == 0 || len(m[0]) == 0 {
        return false
    }
    N := len(m)
    M := len(m[0])
    wlen := len(word)
    // dp[i][j][k]表示：必须以m[i][j]这个字符结尾的情况下，能不能找到w[0...k]这个前缀串
    dp := make([][][]bool, N)
    for i := 0; i < N; i++ {
        dp[i] = make([][]bool, M)
        for j := 0; j < M; j++ {
            dp[i][j] = make([]bool, wlen)
        }
    }
    for i := 0; i < N; i++ {
        for j := 0; j < M; j++ {
            dp[i][j][0] = m[i][j] == word[0]
        }
    }
    for k := 1; k < wlen; k++ {
        for i := 0; i < N; i++ {
            for j := 0; j < M; j++ {
                dp[i][j][k] = m[i][j] == word[k] && checkPrevious(dp, i, j, k)
            }
        }
    }
    for i := 0; i < N; i++ {
        for j := 0; j < M; j++ {
            if dp[i][j][wlen-1] {
                return true
            }
        }
    }
    return false
}

func checkPrevious(dp [][][]bool, i int, j int, k int) bool {
    up := false
    down := false
    left := false
    right := false
    if i > 0 {
        up = dp[i-1][j][k-1]
    }
    if i < len(dp)-1 {
        down = dp[i+1][j][k-1]
    }
    if j > 0 {
        left = dp[i][j-1][k-1]
    }
    if j < len(dp[0])-1 {
        right = dp[i][j+1][k-1]
    }
    return up || down || left || right
}

// 不可以走重复路的设定
func findWord2(m [][]byte, word string) bool {
    if word == "" {
        return true
    }
    if len(m) == 0 || len(m[0]) == 0 {
        return false
    }

    for i := 0; i < len(m); i++ {
        for j := 0; j < len(m[0]); j++ {
            if process(m, i, j, word, 0) {
                return true
            }
        }
    }
    return false
}

// 从m[i][j]这个字符出发，能不能找到w[k...]这个后缀串
func process(m [][]byte, i int, j int, str string, k int) bool {
    if k == len(str) {
        return true
    }
    if i == -1 || i == len(m) || j == -1 || j == len(m[0]) || m[i][j] == 0 || m[i][j] != str[k] {
        return false
    }
    m[i][j] = 0
    ans := false
    if process(m, i+1, j, str, k+1) || process(m, i-1, j, str, k+1) || process(m, i, j+1, str, k+1) || process(m, i, j-1, str, k+1) {
        ans = true
    }
    m[i][j] = str[k]
    return ans
}

执行结果如下：

---

左神java代码