8.26考试总结(NOIP模拟48)[Lighthouse·Miner·Lyk Love painting·Revive]
告诉我,神会流血吗?——神不会,但你会。
前言
我直接打娱乐赛
T1 Lighthouse
解题思路
子集反演(但是 fengwu 硬要说是二项式反演咱也没法。。。)
发现其实 \(m\) 的值非常的小,因此我们可以选择 状压 。
设 \(f_{i}\) 表示将应该删除掉的边至少保留 \(i\) 条的方案数。
那么表示恰好的 \(g_i\) 就可以由子集反演得到,因此最后的答案就是 \(g_0\)
对于当前算到的子集中有超过两条边有公共点,或者两个点之间有超过两种路径就是不合法的,这样显然是构成了环的。
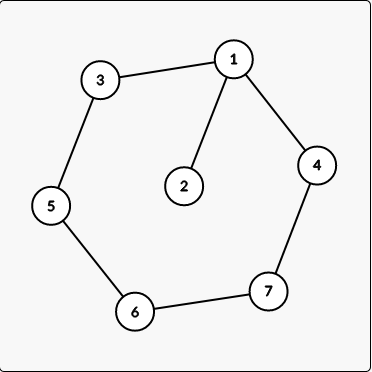
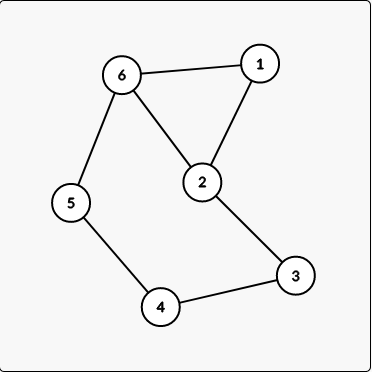
然后如果要构成一个长度为 n 的大环的话,除了当前选到的边,其他的可以直接圆排列。
对于选中的这几条边而言,因为整个图是一个完全图,因此他们的正负都是可以的,因此就有了 \(2^{选中边数}\) 种选择。
但是要注意如果将所有的边都翻转是和不反转一样的,因此需要将方案数除以 2
最后就是特盘一下边的集合组成的是一个长度为 \(n\) 的环的情况就好了。
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e7+10,M=30,mod=1e9+7;
int n,m,top,ans,sta[N],fac[N],p2[N];
int u[M],v[M],vis[N],f[M];
int power(int x,int y)
{
int temp=1;
while(y)
{
if(y&1) temp=temp*x%mod;
x=x*x%mod;
y>>=1;
}
return temp;
}
signed main()
{
n=read();m=read(); fac[0]=p2[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
for(int i=1;i<=n;i++) p2[i]=p2[i-1]*2%mod;
for(int i=1;i<=m;i++) u[i]=read(),v[i]=read();
for(int st=0;st<(1<<m);st++)
{
int e=0,p=0;bool jud=false;
for(int i=1;i<=m;i++)
if((st>>i-1)&1)
{
e++;
if(vis[u[i]]==2||vis[v[i]]==2){jud=true;break;}
if(!vis[u[i]]) p++; vis[u[i]]++;
if(!vis[v[i]]) p++; vis[v[i]]++;
}
for(int i=1;i<=top;i++) if((st&sta[i])==sta[i]){jud=true;break;}
if(e==p&&!jud&&st)
{
jud=true; sta[++top]=st;
if(e==n) f[e]=(f[e]+2)%mod;
}
for(int i=1;i<=m;i++) vis[u[i]]=vis[v[i]]=0;
if(!jud) f[e]=(f[e]+fac[n-e-1]*p2[p-e])%mod;
}
for(int i=0,bas=1;i<=m;i++,bas*=-1) ans=(ans+mod+bas*f[i]*power(2,mod-2)%mod)%mod;
printf("%lld",ans);
return 0;
}
T2 Miner
解题思路
欧拉路,实在是调吐了。。。
对于每一个联通块里的出度奇数点每走一次最多使两个出度为奇数的点变为偶数。
因此,答案就是 \(\sum\limits_{i=1}^{k}\max(1,\dfrac{siz_i}{2})-1\),\(siz_i\) 表示每一个联通块里的出度计数点个数,\(k\) 为联通块个数。
然后对于整个图跑欧拉路,优先跑 出度为奇数 的点。
接下来我就被建边顺序给卡了,然后我就试了一下 random_shuffle 可以获得 \(63pts\sim 84pts\) 不等的分数,主要是他还可能会。。

然后我又试了试将 vector 建边通过翻转变成了前向星建边的顺序,然后发现一直不对的点对了!!!
在然后嘞,测试点分治。。(应该是我的做法有问题。。)
code
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=3e5+10;
int n,m,tot=1,cnt,first,all,Ans,top,sta[N<<1],fa[N],du[N],siz[N],head[N];
pair<bool,int> ans[N<<1];
vector<pair<int,int> > v[N];
bool vis[N<<1],work;
struct Road
{
int l,r;
}pat[N];
void add_edge(int x,int y)
{
v[x].push_back(make_pair(y,++tot));
}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void oula(int fro)
{
bool flag=true,jud=true;
for(int i=head[fro];i<v[fro].size();i++)
if(!vis[v[fro][i].second])
flag=false;
if(flag) return head[fro]=v[fro].size(),void();
ans[++all]=make_pair(1,fro);
int pree=all;
sta[++top]=fro;
Ans--;
while(top)
{
int x=sta[top],pre=top;
if(jud||work||Ans<=0)
for(int i=head[x];i<v[x].size();i++)
{
int to=v[x][i].first;
if(vis[v[x][i].second]){head[x]=i+1;continue;}
vis[v[x][i].second^1]=vis[v[x][i].second]=true;
sta[++top]=to; head[x]=i+1;
du[x]--;du[to]--;
if(to!=x)break;
}
if(pre==top)
{
top--; jud=false;
if(top) ans[++all]=make_pair(0,x);
}
}
reverse(ans+pree+1,ans+all+1);
}
signed main()
{
n=read(); m=read(); srand(time(0));
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1,x,y;i<=m;i++)
{
x=read(); y=read();
pat[i].l=x;pat[i].r=y;
add_edge(pat[i].l,pat[i].r);
add_edge(pat[i].r,pat[i].l);
fa[find(pat[i].l)]=find(pat[i].r);
if(x!=y) du[pat[i].r]++,du[pat[i].l]++;
}
first=pat[1].l;
for(int i=1;i<=n;i++)
if(du[i]&1)
siz[find(i)]++;
for(int i=1;i<=n;i++)
if(find(i)==i&&v[i].size())
Ans+=max(1ll,siz[i]/2);
printf("%lld\n",max(0ll,Ans-1));
for(int i=1;i<=n;i++)
{
if(first!=71131)reverse(v[i].begin(),v[i].end());
for(int j=1,fir=0;j<v[i].size();j++)
{
int to=v[i][j].first;
if(to!=i) continue;
swap(v[i][j],v[i][fir]);
fir++;
}
}
for(int i=1,x,y;i<=m;i++)
if(pat[i].l==pat[i].r)
du[pat[i].l]+=2;
for(int i=1;i<=n;i++)
if(head[i]<v[i].size()&&(du[i]&1))
oula(i);
for(int i=1;i<=n;i++)
if(head[i]<v[i].size()&&du[i])
{
work=true;
oula(i);
}
printf("%lld\n",ans[1].second);
for(int i=2;i<=all;i++)
printf("%d %lld\n",ans[i].first,ans[i].second);
return 0;
}
T3 Lyk Love painting
解题思路
二分答案+DP
考场是是写挂了的,本来想降低一个 \(n\) 的复杂度,没想到弄巧成拙,喜提 \(10pts\)
60pts 的做法是 \(f_{i,j,k}\) 表示第 i 行从 j 到 k 的一段区间内的最优解,更新比较简单,向前跳看区域是否符合当前的二分值就好了。
然后再搞一个 \(g_i\) 表示两行一共到 位置 i 的最小划分数,转移和上面差不多,复杂度 \(n^3log\)
80pts 就比较理智了,先处理出第一行,第二行,两行一共,可以向前跳的最长长度,分别记为 \(f1_i,f2_i,f3_i\)。
然后 \(g_{i,j}\) 表示第一行在 i 位置,第二行在 j 位置的最小划分数。转移就是:
\]
对于 \(i=j\) 的情况还可由 \(g_{f3_i,f3_j}+1\) 转移过来复杂度是 \(n^2log\) 的。
优化一下,发现最大就可以向前面跳 \(m\) 下每次选择下标较大的向前跳,统计答案就好了。
code
60pts
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=1e3+10,INF=1e18;
int n,m,pre[3][N],s[3][N];
int f[3][M][M],g[N];
bool check(int x)
{
memset(f,0x3f,sizeof(f));
memset(g,0x3f,sizeof(g));
g[0]=0;
for(int i=1;i<=2;i++)
for(int l=1;l<=n;l++)
{
f[i][l][l-1]=0;
for(int j=l;j<=n;j++)
for(int k=j-1;k>=l-1;k--)
if(pre[i][j]-pre[i-1][j]-pre[i][k]+pre[i-1][k]<=x) f[i][l][j]=min(f[i][l][j],f[i][l][k]+1);
else break;
}
if(f[1][1][n]+f[2][1][n]<=m) return true;
for(int i=1;i<=n;i++)
for(int j=i-1;j>=0;j--)
if(pre[2][i]-pre[2][j]<=x) g[i]=min(g[i],min(g[j],f[1][1][j]+f[2][1][j])+1);
else g[i]=min(g[i],g[j]+f[1][j+1][i]+f[2][j+1][i]);
if(g[n]<=m) return true;
return false;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=2;i++)
for(int j=1;j<=n;j++)
s[i][j]=read();
for(int i=1;i<=2;i++)
for(int j=1;j<=n;j++)
pre[i][j]=pre[i][j-1]+pre[i-1][j]-pre[i-1][j-1]+s[i][j];
int l=0,r=pre[2][n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
80pts
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=3e3+10,INF=1e18;
int n,m,pre[N],s1[N],s2[N],pre1[N],pre2[N];
int f1[N],f2[N],f3[N],g[M][M];
bool check(int x)
{
memset(g,0x3f,sizeof(g)); g[0][0]=0;
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre1[i]-pre1[j]<=x&&pre1[i]-pre1[j-1]>x)
{
temp=j;
break;
}
if(~temp) f1[i]=temp;
else f1[i]=0;
}
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre2[i]-pre2[j]<=x&&pre2[i]-pre2[j-1]>x)
{
temp=j;
break;
}
if(~temp) f2[i]=temp;
else f2[i]=0;
}
for(int i=1;i<=n;i++)
{
int temp=-1;
for(int j=i;j>=1;j--)
if(pre[i]-pre[j]<=x&&pre[i]-pre[j-1]>x)
{
temp=j;
break;
}
if(~temp) f3[i]=temp;
else f3[i]=0;
}
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
{
if(!i&&!j) continue;
g[i][j]=min(g[f1[i]][j],g[i][f2[j]])+1;
g[i][j]=min(g[i][j],g[max(f1[i],f2[j])][max(f1[i],f2[j])]+2);
if(i==j) g[i][j]=min(g[i][j],g[f3[i]][f3[j]]+1);
}
return g[n][n]<=m;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=n;i++) s1[i]=read();
for(int i=1;i<=n;i++) s2[i]=read();
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+s1[i]+s2[i];
for(int i=1;i<=n;i++) pre1[i]=pre1[i-1]+s1[i];
for(int i=1;i<=n;i++) pre2[i]=pre2[i-1]+s2[i];
int l=0,r=pre[n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
正解
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=1e5+10,M=3e3+10,INF=1e18;
int n,m,pre[N],s1[N],s2[N],pre1[N],pre2[N];
int f1[N],f2[N],f3[N],g[N];
bool check(int x)
{
memset(g,0x3f,sizeof(g)); g[0]=0;
for(int i=1;i<=n;i++)
{
f1[i]=f1[i-1];
for(int j=f1[i]-1;j<i;j++)
if(pre1[i]-pre1[j+1]<=x)
{
f1[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
f2[i]=f2[i-1];
for(int j=f2[i]-1;j<i;j++)
if(pre2[i]-pre2[j+1]<=x)
{
f2[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
f3[i]=f3[i-1];
for(int j=f3[i]-1;j<i;j++)
if(pre[i]-pre[j+1]<=x)
{
f3[i]=j+1;
break;
}
}
for(int i=1;i<=n;i++)
{
g[i]=g[f3[i]]+1;
int pos1=i,pos2=i;
for(int j=1;j<=m&&(pos1||pos2);j++)
{
if(f2[pos2]>f1[pos1]||f1[pos1]==pos1) pos2=f2[pos2];
else pos1=f1[pos1];
g[i]=min(g[i],g[max(pos1,pos2)]+j);
}
}
return g[n]<=m;
}
signed main()
{
n=read(); m=read();
for(int i=1;i<=n;i++) s1[i]=read();
for(int i=1;i<=n;i++) s2[i]=read();
for(int i=1;i<=n;i++) pre[i]=pre[i-1]+s1[i]+s2[i];
for(int i=1;i<=n;i++) pre1[i]=pre1[i-1]+s1[i];
for(int i=1;i<=n;i++) pre2[i]=pre2[i-1]+s2[i];
int l=0,r=pre[n],ans=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
T4 Revive
大坑未补
8.26考试总结(NOIP模拟48)[Lighthouse·Miner·Lyk Love painting·Revive]的更多相关文章
- 20210826 Lighthouse,Miner,Lyk Love painting,Revive
考场 T1 这不裸的容斥 T2 这不裸的欧拉路,先从奇数度点开始走,走不了就传送 T3 什么玩意,暴力都不会 T4 点分树??? 仔细想了一波,发现 T1 T2 都好做,T3 二分答案后可以暴力贪心, ...
- 2021.9.26考试总结[NOIP模拟62]
T1 set 从\(0\)到\(n\)前缀余数有\(n+1\)个,但只有\(n\)种取值,找到一样的两个输出区间即可. \(code:\) T1 #include<bits/stdc++.h&g ...
- 6.17考试总结(NOIP模拟8)[星际旅行·砍树·超级树·求和]
6.17考试总结(NOIP模拟8) 背景 考得不咋样,有一个非常遗憾的地方:最后一题少取膜了,\(100pts->40pts\),改了这么多年的错还是头一回看见以下的情景... T1星际旅行 前 ...
- 5.23考试总结(NOIP模拟2)
5.23考试总结(NOIP模拟2) 洛谷题单 看第一题第一眼,不好打呀;看第一题样例又一眼,诶,我直接一手小阶乘走人 然后就急忙去干T2T3了 后来考完一看,只有\(T1\)骗到了\(15pts\)[ ...
- 5.22考试总结(NOIP模拟1)
5.22考试总结(NOIP模拟1) 改题记录 T1 序列 题解 暴力思路很好想,分数也很好想\(QAQ\) (反正我只拿了5pts) 正解的话: 先用欧拉筛把1-n的素数筛出来 void get_Pr ...
- 2021.9.17考试总结[NOIP模拟55]
有的考试表面上自称NOIP模拟,背地里却是绍兴一中NOI模拟 吓得我直接文件打错 T1 Skip 设状态$f_i$为最后一次选$i$在$i$时的最优解.有$f_i=max_{j<i}[f_j+a ...
- [考试总结]noip模拟23
因为考试过多,所以学校的博客就暂时咕掉了,放到家里来写 不过话说,vscode的markdown编辑器还是真的很好用 先把 \(noip\) 模拟 \(23\) 的总结写了吧.. 俗话说:" ...
- noip模拟48
A. Lighthouse 很明显的容斥题,组合式与上上场 \(t2\) 一模一样 注意判环时长度为 \(n\) 的环是合法的 B. Miner 题意实际上是要求偶拉路 对于一个有多个奇数点的联通块, ...
- [考试总结]noip模拟26
首先看到这样中二的题目心头一震.... 然而发现又是没有部分分数的一天. 然而正解不会打.... 那还是得要打暴力. 但是这套题目有两个题目只有一个参数. 所以... (滑稽).jpg 然后我就成功用 ...
- 2021.7.28考试总结[NOIP模拟26]
罕见的又改完了. T1 神炎皇 吸取昨天三个出规律的教训,开场打完T2 20pts直接大力打表1h. 但怎么说呢,我不懂欧拉函数.(其实exgcd都忘了 于是只看出最大平方因子,不得不线性筛,爆拿60 ...
随机推荐
- spring boot @propertySource @importResource @Bean [六]
@propertySource 指定property的配置源. 创建一个person.property: 然后修改person注解; 在运行test之后,结果为: @importResource 这个 ...
- VScode 使用emmet
背景 在很多的编辑场合,很多时候回出现很多逻辑性的问题.可能觉得html是一门没有逻辑的语言,实际上,它是有一定的思想编辑的.后来出现了emmet,这个不仅仅是一种快捷方式,同时也是一种思考方式. 解 ...
- Python - PEP572: 海象运算符
海象运算符 PEP572 的标题是「Assignment Expressions」,也就是「赋值表达式」,也叫做「命名表达式」 不过它现在被广泛的别名是「海象运算符」(The Walrus Opera ...
- 2024-04-17:用go语言,欢迎各位勇者莅临力扣城,本次的挑战游戏名为「力扣泡泡龙」。 游戏的起点是一颗形状如二叉树的泡泡树,其中每个节点的值代表该泡泡的分值。勇者们有一次机会可以击破一个节点泡
2024-04-17:用go语言,欢迎各位勇者莅临力扣城,本次的挑战游戏名为「力扣泡泡龙」. 游戏的起点是一颗形状如二叉树的泡泡树,其中每个节点的值代表该泡泡的分值.勇者们有一次机会可以击破一个节点泡 ...
- 阿里云2020上云采购季,你的ECS买好了吗?
阿里云2020上云采购季,超级品类日,天天有爆款. 今日爆款推荐:云服务器. 重磅推荐两款,限时抢购. 新品共享型s6: 企业级共享型n4: 想看更多云产品,来阿里云采购季: https://www. ...
- 重温设计模式之 Factory
简介: 创建型模式的核心干将,工厂.简单工厂.抽象工厂,还记得清么,一文回顾和对比下. 作者 | 弥高来源 | 阿里技术公众号 前言 创建型模式的核心干将,工厂.简单工厂.抽象工厂,还记得清么,一文回 ...
- WPF 简单实现一个支持删除自身的应用
我准备写一个逗比的应用,然而我担心被小伙伴看到这个应用的文件从而知道是我写的,于是我就需要实现让应用能自删除的功能.核心实现方法就是调用 cmd 传入命令行,等待几秒之后删除文件 应用程序在运行时,是 ...
- Java根据URL截图的4种方式
方案选择 XHTMLRenderer(不要用) PhantomJs(三方库,已停更) Puppeteer(Chrome团队开发和维护) Selenium(支持多浏览器.多语言,服务器需要安谷歌浏览器) ...
- EPAI手绘建模APP资源管理和模型编辑器2
g) 矩形 图 26模型编辑器-矩形 i. 修改矩形的中心位置. ii. 修改矩形的长度和宽度. h) 正多边形 图 27模型编辑器-内接正多边形 图 28模型编辑器-外切正多边形 i. 修改正多 ...
- SAP Adobe Form 几种文本类型
前文: SAP Adobe Form 教程一 简单示例 SAP Adobe Form 教程二 表 SAP Adobe Form 教程三 日期,时间,floating field SAP Adobe F ...
