曲线艺术编程 coding curves 第十一章 玫瑰花形（ ROSES）

第十一章 玫瑰花形 ROSES

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

译者：池中物王二狗(sheldon)

源码：github: https://github.com/willian12345/coding-curves

曲线艺术编程系列第 11 章

这一篇我们将看到另一种我钟意的曲线类型 -- 玫瑰花形或玫形曲线。 在我看来这类曲线就像是圆形的利萨茹曲线 Lissajous curves，或者非常规则的谐波图。事实上它们是一类特别的长短幅内摆线，特别到足够自成一类。先给你看些例子，下面是玫形曲线：

（译都注：这是玫瑰花 roses 我是不信的...）

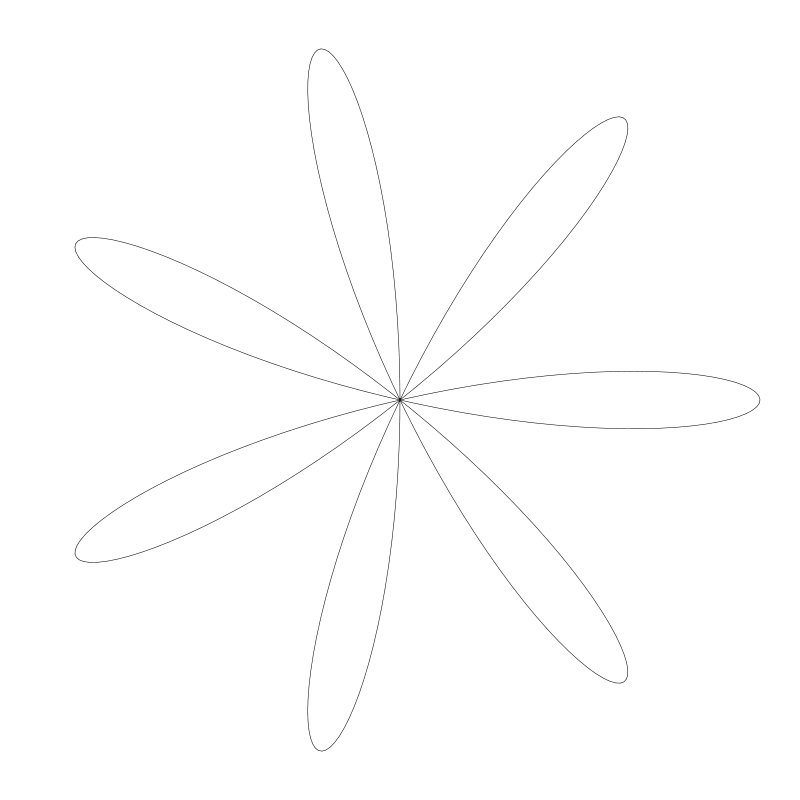
就像其它我们关注过的其它曲线一样，我们有参数方程, 用 t 从 0 到 2 * PI 递增，计算得到返回值并用它绘制出曲线。我们先往回看看圆的方程：

function circle(x, y, r) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    x1 = x + cos(t) * r
    y1 = y + sin(t) * r
    lineTo(x1, y1)
  }
}

你当然可以对 for 循环内的代码简化成一行，但为了解释的更清晰我还是将它展开了。

一个玫瑰花形曲线使用同样的策略，但使用以 t 和其它参数为基础的动态半径取代固定的半径。下面是半径方程：

r = a * cos(n * t)

现在我们有了 2 个新变量。a 是花的覆盖半径， n 控制着花瓣数（当然花瓣数量的计算有点儿复杂，捎后回来解释）。现在我们可以创建一个玫瑰花形函数：

function rose(x, y, a, n) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n * t)
    x1 = x + cos(t) * r
    y1 = y + sin(t) * r
    lineTo(x1, y1)
  }
}

当然如果你愿意，可以整理一下代码：

function rose(x, y, a, n) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

现阶段先假设函数的 n 参数为正整数。当然后面我们也会探索更大的范围。

现在我们就可以绘制我们第一个玫瑰花形：

width = 800
height = 800
canvas(800, 800)

rose(width / 2, height / 2, width * 0.45, 5)
stroke()

在这里我会经常用 width * 0.45。它刚好比 canvas 宽度的一半小一点儿，这让曲线几乎刚好覆盖整个 canvas 但又没能碰到边界。

上面代码会生成一个 5 个花瓣的玫瑰花形：

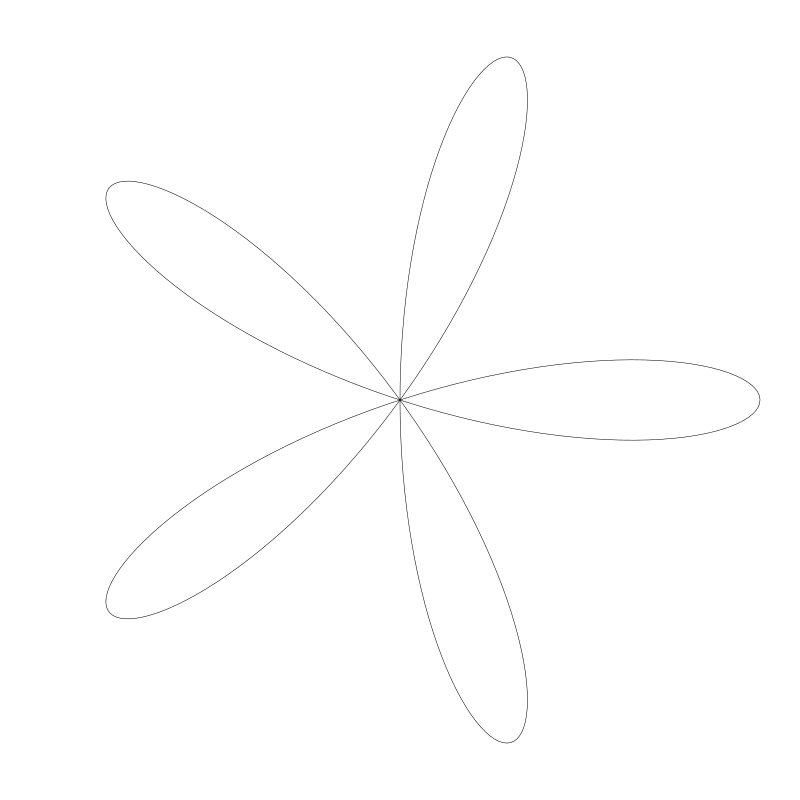
第一个例子中 n 用的是 7。 而下面这个花 n 用的是 11：

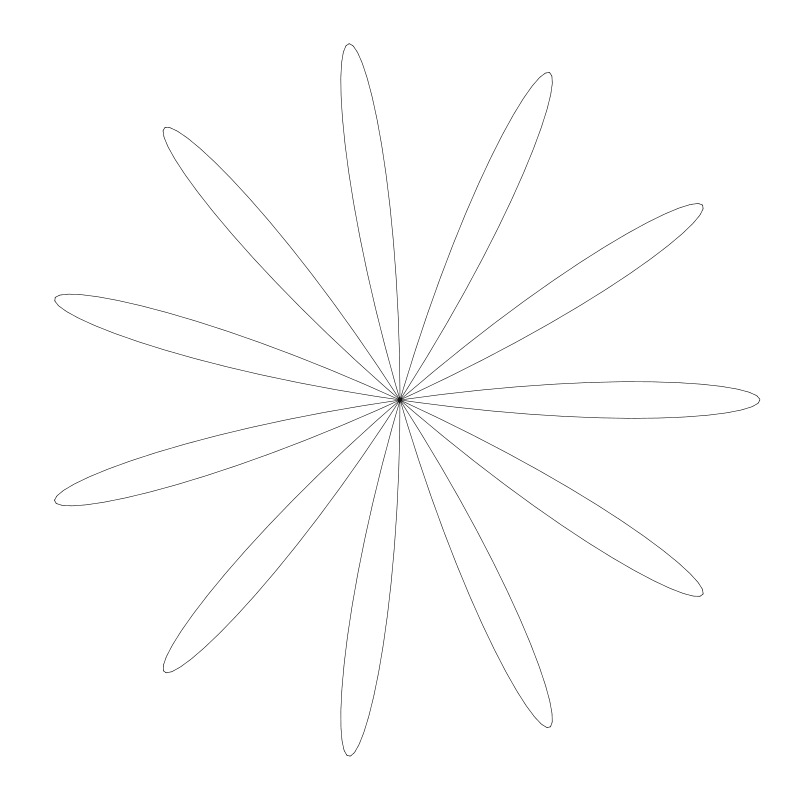
到目前为止我们可以看到 n 与 花瓣数量之间有很好的相关性。前面 n 用的都是奇数。如果我们用的是偶数 n 为 4 会如何呢？

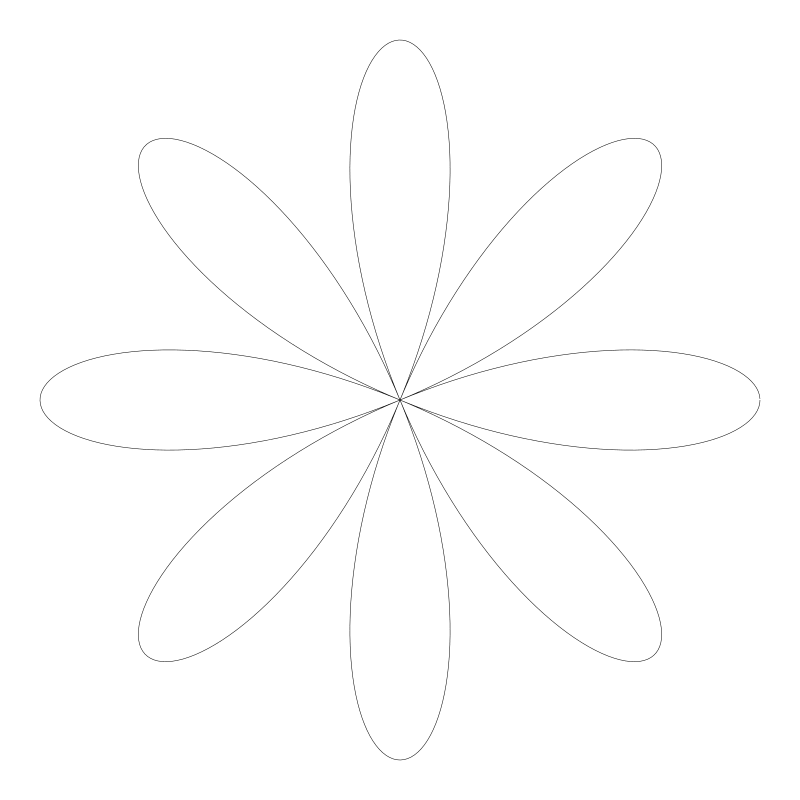
有意思，产生了 8 个花瓣。n 的值遵循 奇数 n 创建 n 个花瓣。 偶数 n 创建 2 * n 个花瓣。把 n 再设大一点看看，设 n = 40，它将产生 80 个花瓣。我不得不提升辨率 -- 将循环上的 t 改为 0.001 以保证花瓣没有锯齿。

相反，如果 n = 1，仅会得到一个单圆

有点怪，但在数学上说得通。你会发现 n 为负值时，玫瑰花看起来与 n 为正值时得到的结果图形一样。 下面左边的是 5 右边的是 -5

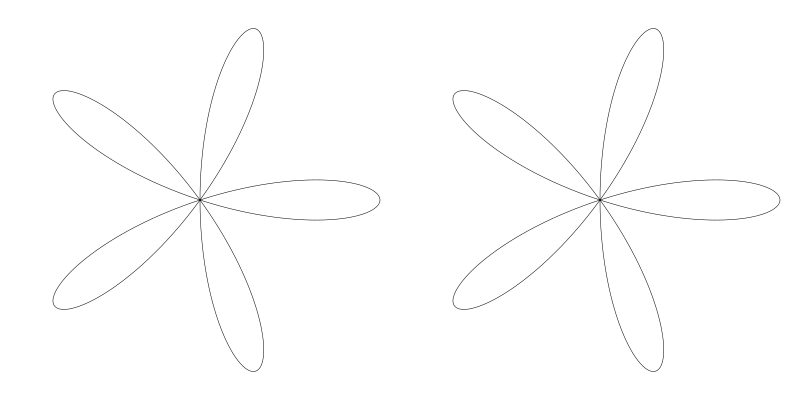
毫无意外， n = 0 时会得不到任何图形。并且我们已经覆盖了全部的整数玫瑰花形。如果这是全部了的话就太好了。可惜还有更多的类型。

（译者注：如果你用 javascript 代码实现测试，你会发现 n = 0 时你会画出一个大圆，n = 1 时是右侧一个小圆，

可用源码 https://github.com/willian12345/coding-curves/tree/main/examples/ch11/rose-3.html 测试）

交替玫瑰花形

在我讲完所有 n 值前， 我想先提一下交替玫瑰方程。在半径方程中用正弦 sine 代替余弦 cosine ：

r = a * sin(n * t)

它会生成与原来一样的花形，但是旋转了。左侧是用余弦 5 个花瓣的原图， 右侧是用正弦：

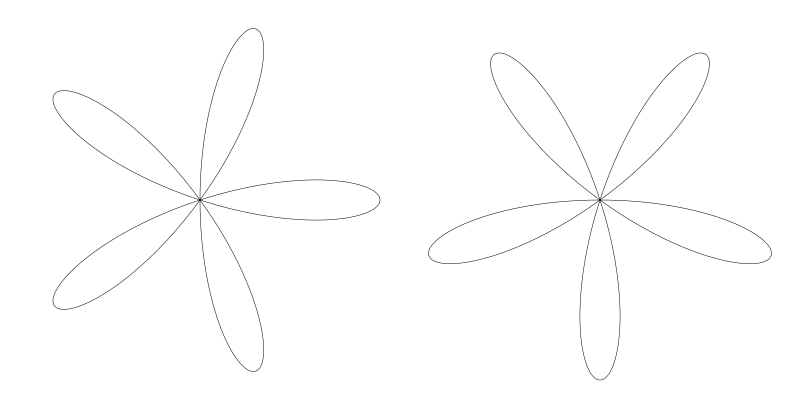
8 个花瓣的也是一样的效果 （n = 4）

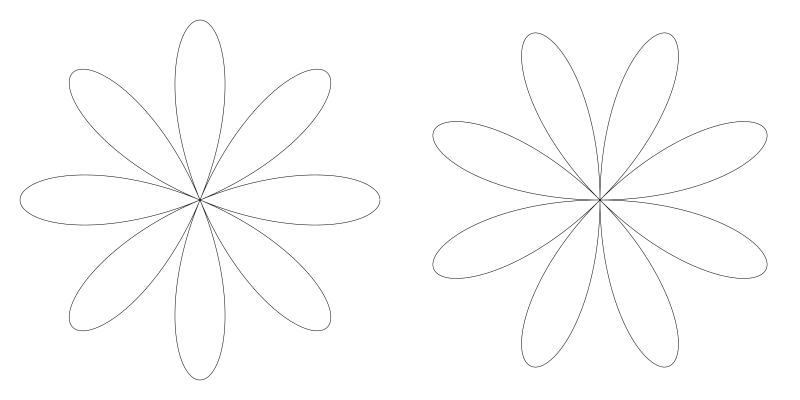
真实的旋转值是 PI / （2 * n) 弧度, 或 90 / n 度。n 为奇数时，视觉上看起来总是旋转了 90 度 （实际旋转可能不同，但由于旋转对称性，它看起来就像是旋转了90度）。当 n 为偶数时花瓣就会在原版本花瓣之间。

当 n 为分数

当我们给 n 的值是分数时事情就变的更有趣了。我们可以试着用分数生成玫瑰花 ：

rose(width/2, height/2, width * 0.45, 5.0 / 4.0)
stroke()

但是结果越令人相当失望

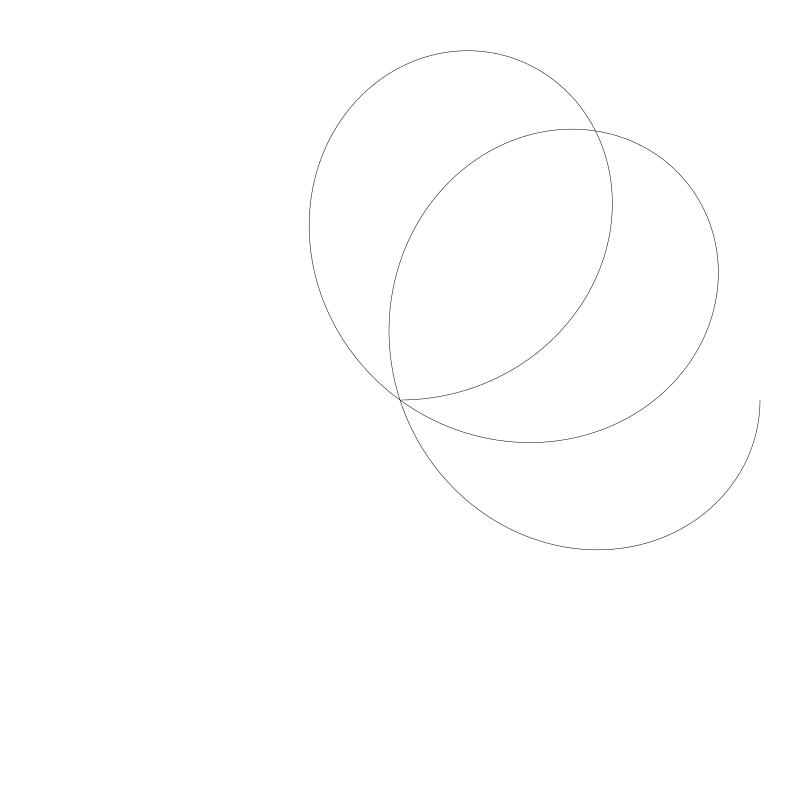
问题在于它需要超过 2 * PI 以获取整圆。那么要超过多少呢？ 好吧，我们用编程的方式来解决，我们首先需要确保 n 为有理数。如果它是无理数， 这朵玫瑰花就会无法闭合回起点（译者注：绕多少圈圆也无法与起始点相接）。我们也需要知道分数的分子与分母。我们可以通过调整玫瑰花形生成函数，为其额外添加一个参数，我们将 n 作为分子，d 作为分母。

rose(x, y, a, n, d) {
  for (t = 0; t < 2 * PI; t += 0.01) {
    r = a * cos(n / d * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

调整后的函数暂时还没有解决问题，但这是解决问题的第一步。你可以强制 n 和 d 为整数，以确保得到有理数分数（译者注：数学上，有理数是一个整数 a 和一个 正整数 b 的比）， 但确保相除前转换它们以保证它返回值为浮点数。

现在需要调整 for 循环 2*PI 的结束条件为我们需要的值。 这个范围值是：

limit = PI * d * m

但是这个新的 m 变量是什么？如果 d * n 结果为奇数则 m 应该为 1。如果 d * n 结果为偶数则 m 应该为 2。 Woo! 有点儿复杂了.. 别担心我们可以简化它。

我们通常将数对2取余来判断数的奇偶性。如果结果为 0 ，则这个数是偶数，如果结果为 1 则原值为奇数。 我们想：

m = 1 when d * n % 2 == 1

并且

m = 2 when d * n % 2 == 0

所以我们可以这样设置：

（译者注： d * n % 2 == 1 奇数 m = 1; d * n % 2 == 0 偶数 m = 2; ）

m = 2 - d * n % 2

下面是修改后的函数：

rose(x, y, a, n, d) {
  m = 2 - d * n % 2
  limit = PI * d * m
  for (t = 0; t < limit; t += 0.01) {
    r = a * cos(n / d * t)
    lineTo(x + cos(t) * r, y + sin(t) * r)
  }
}

记住，如果 n 和 d 强制为整数， 为了保证运行正常你可能需要对它们强制转换。我将这部分工作留给你们自己完成 。现在我们可以重新调用：

rose(width/2, height/2, width * 0.45, 5, 4)
stroke()

现在得到的结果就好多了：

（译者注：可用源码 https://github.com/willian12345/coding-curves/tree/main/examples/ch11/rose-6.html 测试）

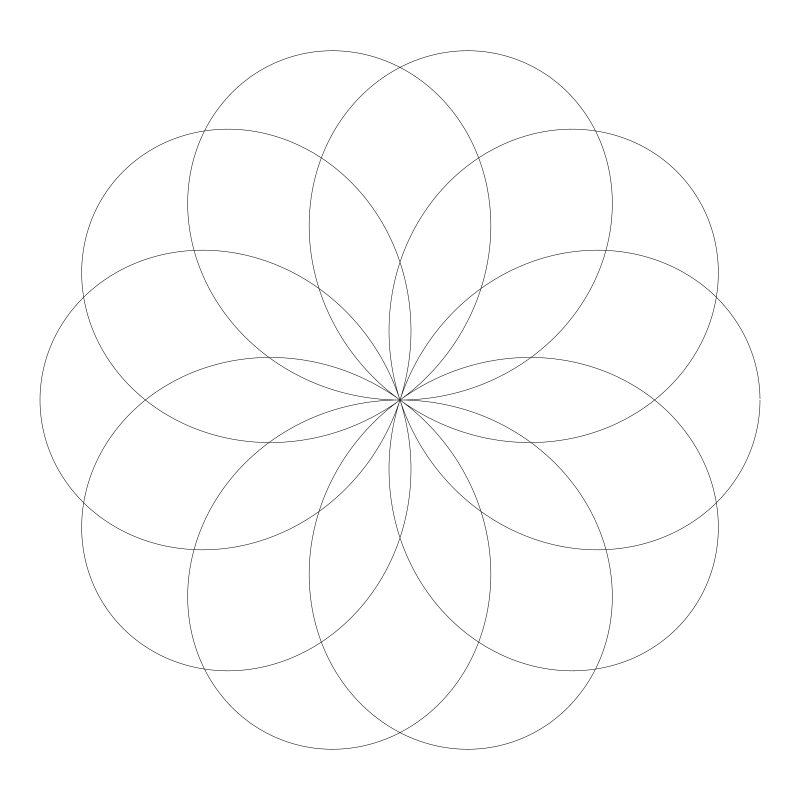
这回这玫瑰花算是完整了。

现在你可以用不同的分数来测试下效果了。我发现如果分子分母值大但相互很接近会生成非常有趣的数。举个例子， n = 22, d = 21:

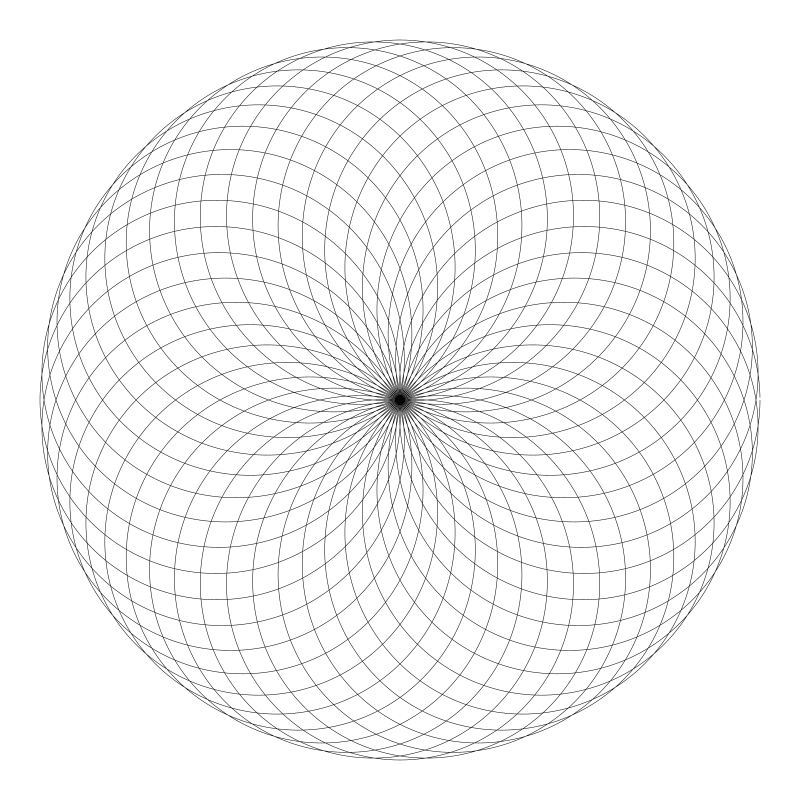
甚至是 81 和 80：

当分数小于 1.0 时图形变得完全不同但依然很有趣。举个例子，下图左侧图形 n 和 d 分别为 1，2，中间图形是 1，3， 右侧图形 1，4。

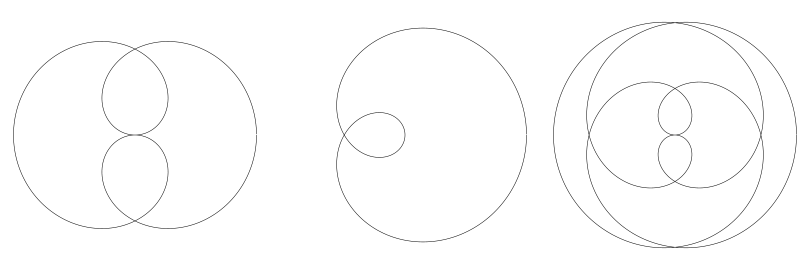
有个找到有趣图案的小技巧是可以对的这对值可以化简，比如 17 / 51 可以化简成 1 / 3, 结果图形就是上图的中间那一幅。当改动一点点其中的某个值时，比如变成 17 / 52:

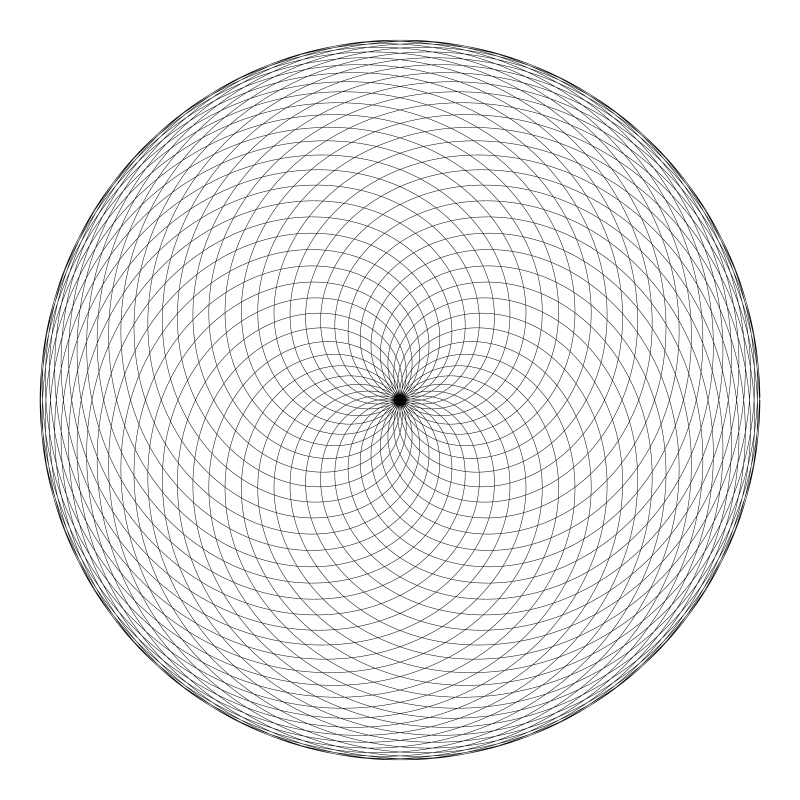
变动了 1 但造成的结果差异非常大。

有些特别的玫瑰曲线拥有自己的名称。我分享几个给你们。

蚶线三分角 （Limaçon Trisectrix）

n / d 是 1 / 3, 我们在前面已经见过了。

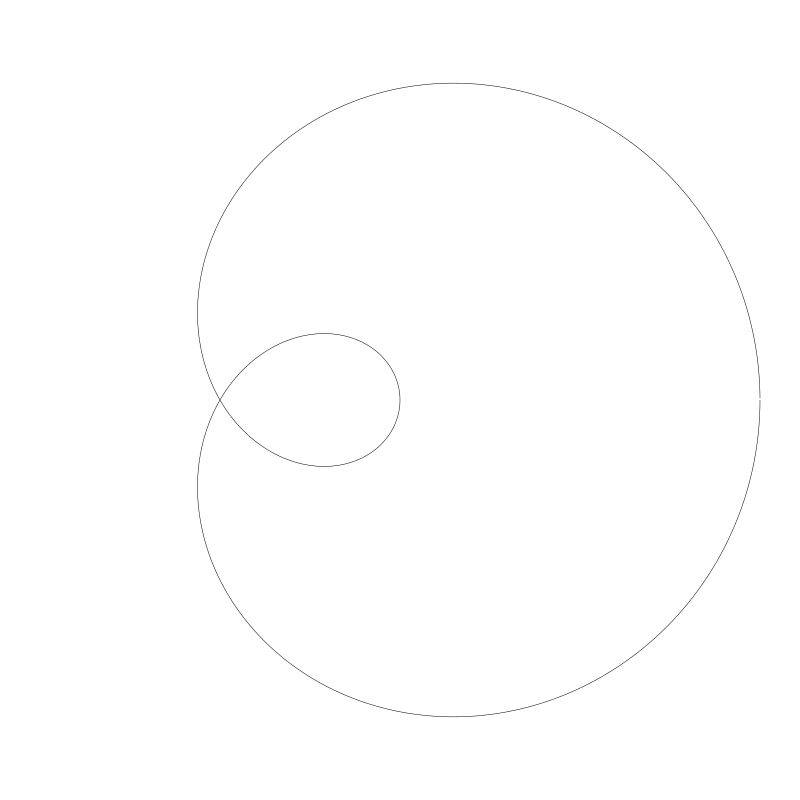
杜勒叶形线 （Dürer Folium）

n / d 是 1 / 2, 之前也见过了

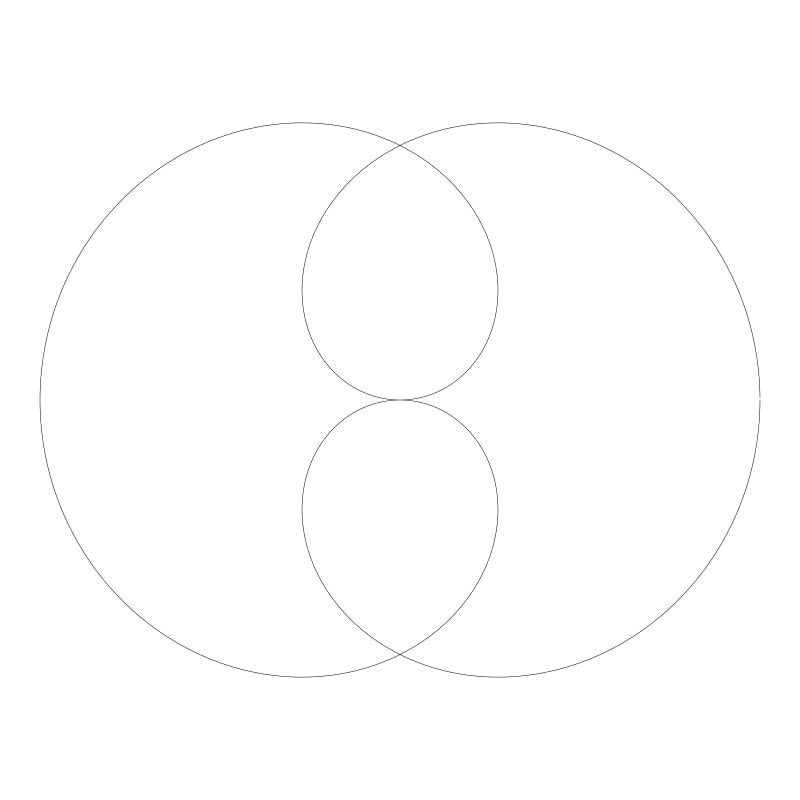
四叶玫瑰线（Quadrifolium）

比例是 2 / 1

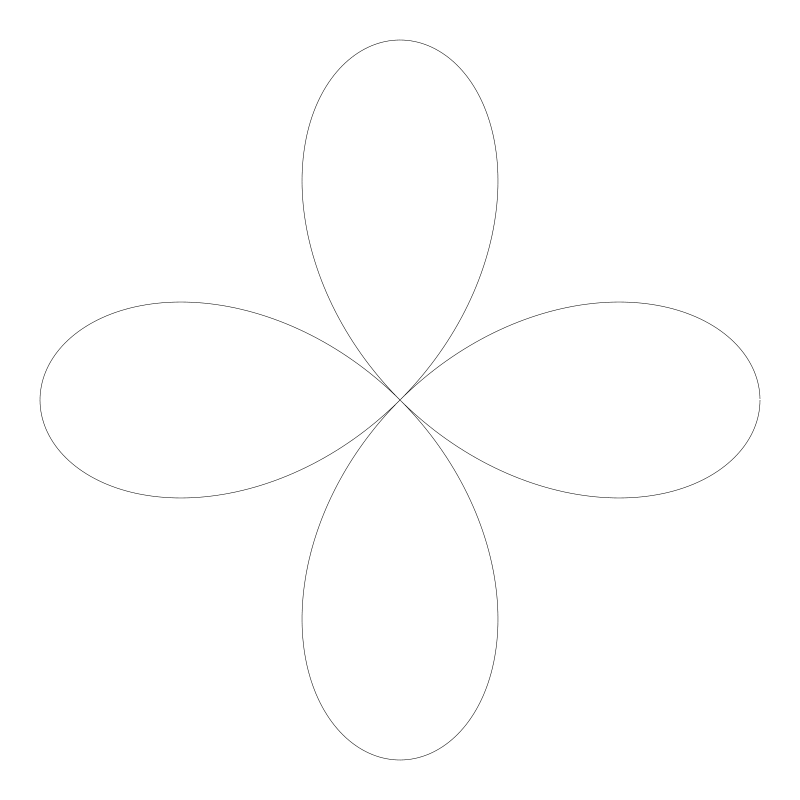
三叶玫瑰线（Quadrifolium）

比例是 3 / 1

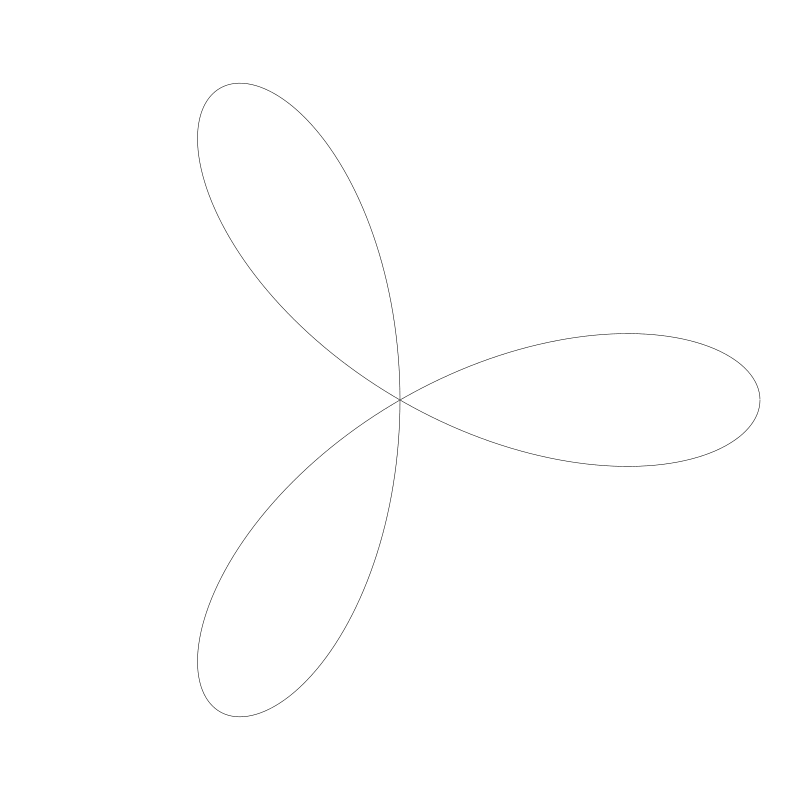
毛雷尔玫瑰（Maurer Roses）

你以为我们这就结束了？错！还有其它类型的玫瑰形曲线等我们探索呢 -- 毛雷尔玫瑰（Maurer Roses）！

毛雷尔玫瑰 建立在 rose 函数基础上， 与一直绘制曲线不同的是，它绘制的是一系列线段将延玫瑰曲线上的点连接起来。通常使用 360 个特殊角度的线段绘制，虽然这不是必须的。 我们先用比例为 4 / 1 建个玫瑰图， 然后挑一个角度值用于循环内。此例中我使用的是 49。然后我们使用 t 循环 0 到 360度，将 t 乘以这个角度值。 所以 t 会从 0 递增， 到 49, 98, 147, 196 继续往后。我们在我们的玫瑰曲线的下一个点上应用（当然角度要转变成弧度）。下面这个 gif 图 表现的是前 30 次循环时的画面。

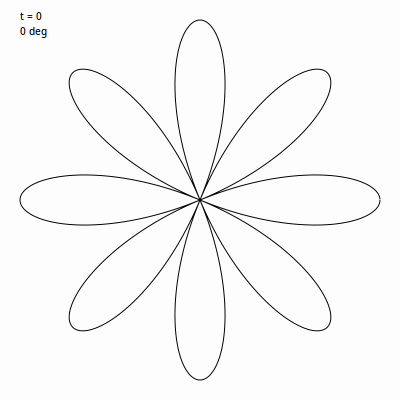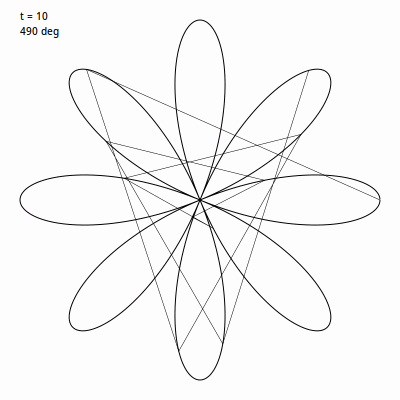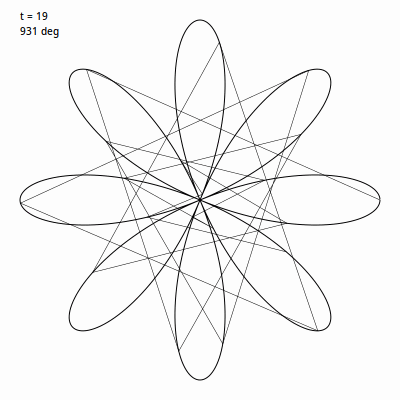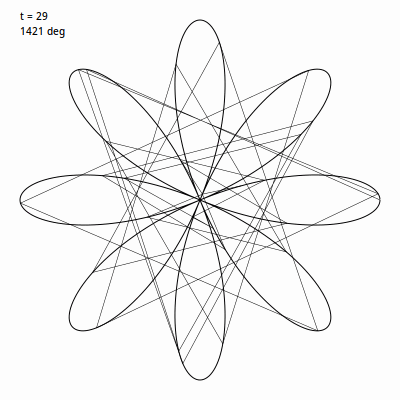
换种说法，在普通的玫瑰曲线中，递增间隔非常非常小，所以我们可以得到一个非常平滑的曲线。这里我们递增间隔巨大，这会让图看起来乱糟糟的。但是，我们等它完成 360 次迭代路径绘制完成，将会得到：

Aha! 全部完成后线条竟然不乱了！事实上，看起来还挺不错。上面我在毛雷尔玫瑰上还绘制了标准玫瑰图。但下面这个才是毛雷尔玫瑰的全貌：

我觉得两个图组合起来还挺好看。

所以具体怎么做呢？

我们还是得从基础的 rose 函数开始。 但这次，我们使用单个整数值。所以只有参数 n 没有参数 d 了。我们还要指定每次迭代角度的递增值。为了避免与之前 d 参数混淆，将参数名改成 deg 。这个函数签名是：

function maurer(x, y, a, n, deg)

还有，我们希望将 t 从 0 循环至 360。然后将 t 乘以 deg 。这就是角度了就像之前动画时那样。我们将它设为变量 k ，但在此之前还需要乘以 PI 再除以 180 转换成弧度

function maurer(x, y, a, n, deg) {
  for (t = 0; t < 360; t++) {
    k = t * deg * PI / 180
    r = a * cos(n * k)
    lineTo(x + cos(k) * r, y + sin(k) * r)
  }
}

我们用 k 代替之前的 t 后执行 rose 算法。

现在我们可以像下面这样调用函数了：

width = 800
height = 800
canvas(800, 800)

maurer(width / 2, height / 2, width * 0.45, 5, 37)
stroke()

// drawing the regular rose is optional
// 标准玫瑰图可画可不画
rose(width / 2, height / 2, width * 0.45, 5, 1)
stroke()

得到：

对 n 和 deg 用不同的值试试。你会发现 n 的作用与前面标准玫瑰图形一样。但是变量 deg 即便是微小的变化都能让图形完全不同。 例如，在这个图形中，n 为 7 且 deg 为 23：

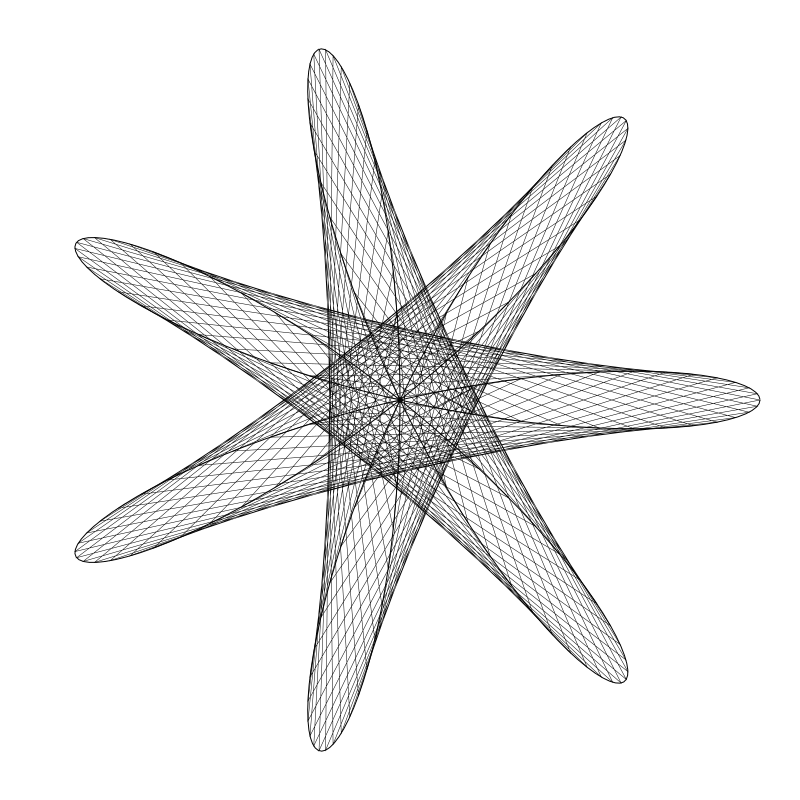
但将 deg 变为 24 时会得到下面这样的结果：

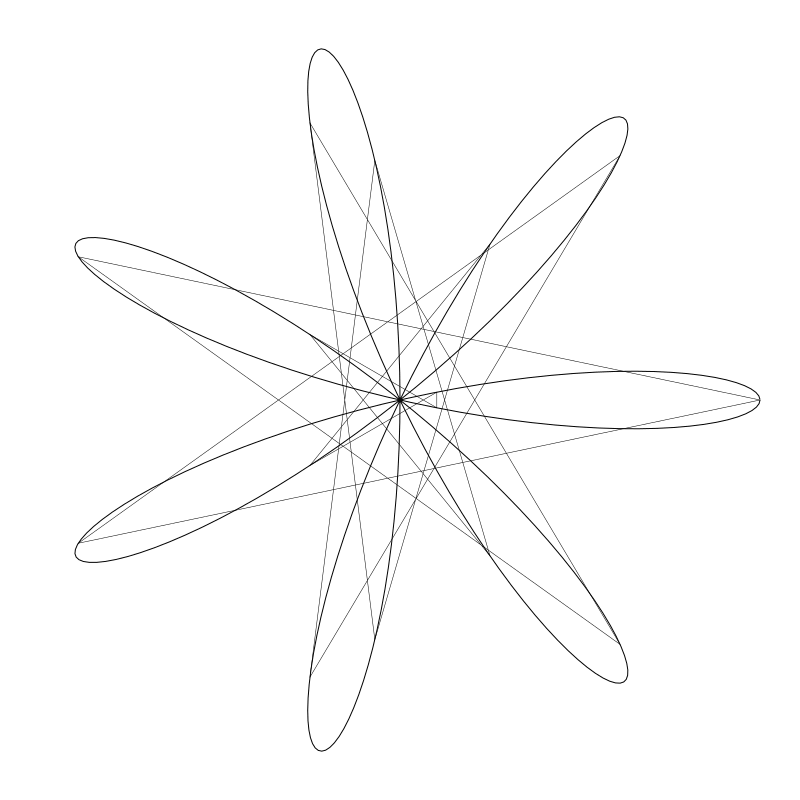
显然没那么好看了。

一般来说，变量 deg 使用奇数会比偶数时要好（当然也有例外）。

任何能被 360 整除的整数都不太行。举个例子， 4， 120：

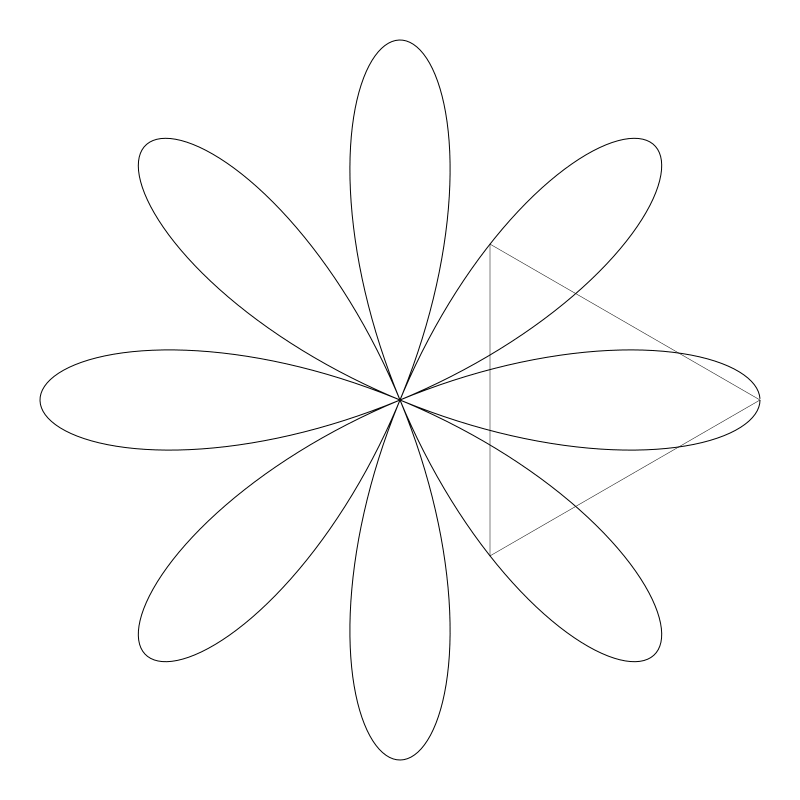
我还是绘制了完整的图，但毛雷尔图形却仅仅绘制成了右边一个三角形。 于是将值增大到 121， 这回可就好多了：

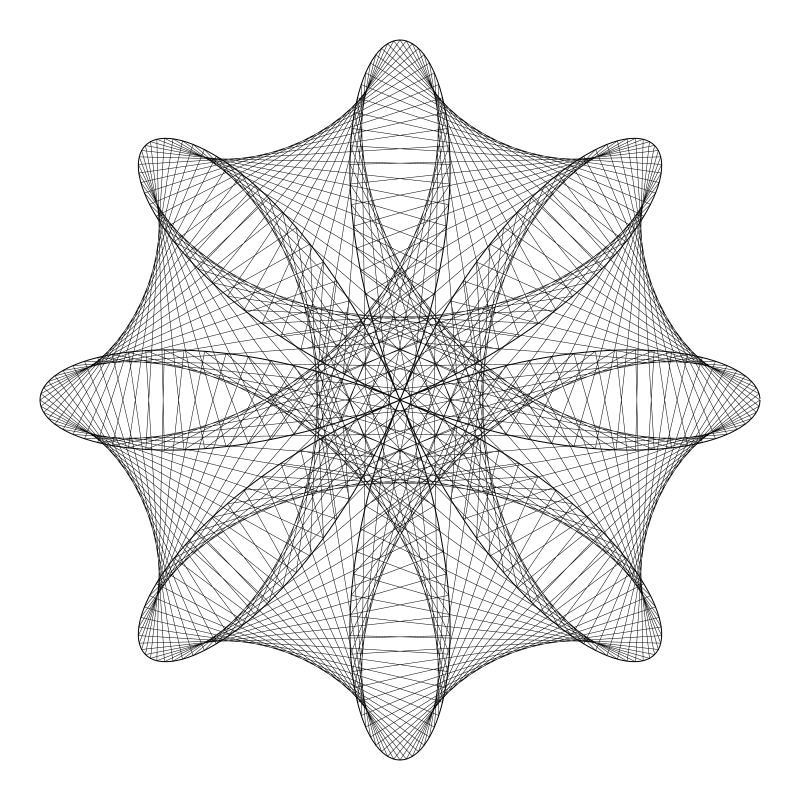
而且，较小的质数通常都都能得到较漂亮的图形。 我注意到如果 n 值够小那么 deg 质数大一点儿最后的效果也还行。 我还没有完整验证过。我要多尝试测试下。

还有一项你可能想尝试的东西，就是给毛雷尔玫瑰用分数值。你完全不用改动函数。 你就直接传一个分数值给 maurer 函数。 因为我们总是从0 循环至 360， 我们不需要调整循环范围。下面是个传分数值的例子，注意在给 rose 函数传递时两个参数还是分开传的。

maurer(0, 0, width * 0.45, 5.0 / 4.0, 229)
stroke()
rose(0, 0, width * 0.45, 5, 4)
stroke()

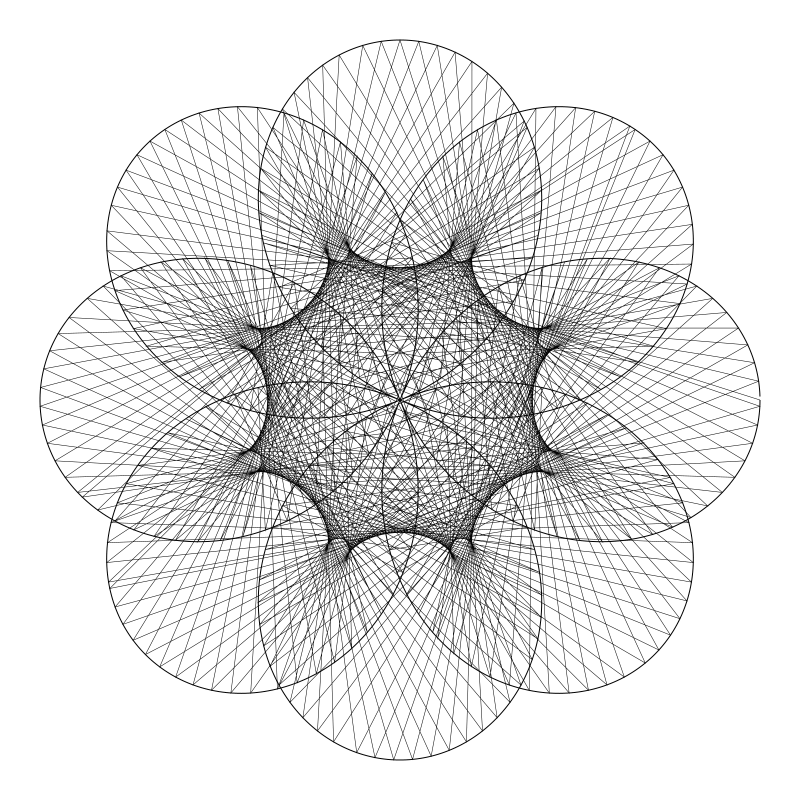
看看你能在所有可能的图形变化中找到什么。

本章 Javascript 源码 https://github.com/willian12345/coding-curves/blob/main/examples/ch11

---

博客园: http://cnblogs.com/willian/

github: https://github.com/willian12345/