bzoj 1195

http://www.lydsy.com/JudgeOnline/problem.php?id=1195

状压DP。

首先去掉被包含的字符串。

对于字符串i和j，我们求出 当字符串j的左端点在字符串i的左端点的左边或与字符串i的左端点重合时，字符串i和字符串j可以重合的最长长度cost是多少。

就是求下面红色部分的最长长度cost：

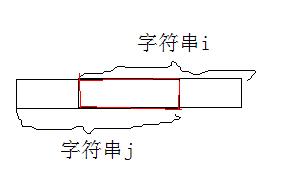
这个强行枚举就可以了，反正数据这么小。

注意，因为我们已经去掉了被包含的字符串，所以不会出现下面这种情况：

所以去掉了被包含的字符串是为了保证当左端点单调时，右端点也是单调的。

建一个图，我们在图中i连到j一条费用为cost的有向边。

然后就是求不重复经过点，可以走的最长路径。

这是哈密顿路径问题，为NP问题，但是这道题数据范围很小，可以用状压DP。

对于输出字典序最小字符串那里，我们在找决策的时候比较一下即可。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<fstream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<utility>
#include<set>
#include<bitset>
#include<vector>
#include<functional>
#include<deque>
#include<cctype>
#include<climits>
#include<complex>
//#include<bits/stdc++.h>适用于CF,UOJ，但不适用于poj

using namespace std;

typedef long long LL;
typedef double DB;
typedef pair<int,int> PII;
typedef complex<DB> CP;

#define mmst(a,v) memset(a,v,sizeof(a))
#define mmcy(a,b) memcpy(a,b,sizeof(a))
#define fill(a,l,r,v) fill(a+l,a+r+1,v)
#define re(i,a,b)  for(i=(a);i<=(b);i++)
#define red(i,a,b) for(i=(a);i>=(b);i--)
#define ire(i,x) for(typedef(x.begin()) i=x.begin();i!=x.end();i++)
#define fi first
#define se second
#define m_p(a,b) make_pair(a,b)
#define SF scanf
#define PF printf

template<class T>inline T sqr(T x){return x*x;}
template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;}
template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;}

const DB EPS=1e-;
inline int sgn(DB x){if(abs(x)<EPS)return ;return(x>)?:-;}
const DB Pi=acos(-1.0);

inline int gint()
  {
        int res=;bool neg=;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return ;
        if(z=='-'){neg=;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
        return (neg)?-res:res;
    }
inline LL gll()
  {
      LL res=;bool neg=;char z;
        for(z=getchar();z!=EOF && z!='-' && !isdigit(z);z=getchar());
        if(z==EOF)return ;
        if(z=='-'){neg=;z=getchar();}
        for(;z!=EOF && isdigit(z);res=res*+z-'',z=getchar());
        return (neg)?-res:res;
    }

const int maxN=;
const int maxlen=;

int N;
char s[maxN+][maxlen+];

int tempN;
char temps[maxN+][maxlen+];
int f[maxN+];

inline int smaller(char *s1,char *s2,int l1,int l2)
  {
      int i,len1=strlen(s1+),len2=strlen(s2+);
      re(i,,min(len1-l1+,len2-l2+))if(s1[l1+i-]!=s2[l2+i-])return s1[l1+i-]<s2[l2+i-];
      return len1-l1+<len2-l2+;
  }

inline int same(char *s1,char *s2,int l1,int l2,int len)
  {
      int i;
      if(l1+len->strlen(s1+))return ;
      if(l2+len->strlen(s2+))return ;
      re(i,,len)if(s1[l1+i-]!=s2[l2+i-])return ;
      return ;
  }

inline int check(char *s1,char *s2)
  {
      int i,l1=strlen(s1+),l2=strlen(s2+);
      re(i,,l2-l1+)if(same(s1,s2,,i,l1))return ;
      return ;
  }

int now,first[maxN+];
struct Tedge{int v,cost,next;}edge[maxN*maxN+];
inline void addedge(int u,int v,int cost){now++;edge[now].v=v;edge[now].cost=cost;edge[now].next=first[u];first[u]=now;}

#define two(k) (1<<((k)-1))
#define wei(v,k) ((v>>(k-1))&1)

int F[maxN+][(<<maxN)+],vis[maxN+][(<<maxN)+];
int head,tail;PII que[maxN*(<<maxN)+];

int cnt;char out[maxN*maxlen+];

int main()
  {
      /*freopen("substr.in","r",stdin);
      freopen("substr.out","w",stdout);*/
      int i,j;
      N=gint();
      re(i,,N)SF("%s\n",s[i]+);
      re(i,,N)re(j,,N)if(i!=j)if(check(s[i],s[j])){f[i]=;break;}
      mmcy(temps,s);
        tempN=N;N=;
      re(i,,tempN)if(!f[i])mmcy(s[++N],temps[i]);
      if(N==)N=;

      now=-;mmst(first,-);
      re(i,,N)re(j,,N)if(i!=j)
        {
            int leni=strlen(s[i]+),lenj=strlen(s[j]+),res=lenj;
            while(res!= && !same(s[i],s[j],,lenj-res+,res))res--;
            addedge(i,j,res);
        }

      mmst(F,-);mmst(vis,);
      head=;tail=-;
      re(i,,N)F[i][two(i)]=,vis[i][two(i)]=,que[++tail]=PII(i,two(i));
      while(head<=tail)
        {
            int u=que[head%(maxN*(<<maxN)+)].fi,state=que[head%(maxN*(<<maxN)+)].se,v,cost;head++;
            vis[u][state]=;
            for(i=first[u],v=edge[i].v,cost=edge[i].cost;i!=-;i=edge[i].next,v=edge[i].v,cost=edge[i].cost)
              if(!wei(state,v) && F[u][state]+cost>F[v][state+two(v)])
                {
                    F[v][state+two(v)]=F[u][state]+cost;
                    if(!vis[v][state+two(v)])
                      {
                          vis[v][state+two(v)]=;
                          que[(++tail)%(maxN*(<<maxN)+)]=PII(v,state+two(v));
                      }
                }
        }

      now=-;mmst(first,-);
      re(i,,N)re(j,,N)if(i!=j)
        {
            int leni=strlen(s[i]+),lenj=strlen(s[j]+),res=lenj;
            while(res!= && !same(s[i],s[j],,lenj-res+,res))res--;
            addedge(j,i,res);
        }

      int u=-,state=two(N+)-;
      re(i,,N)if(u==- || F[u][state]<F[i][state] || (F[u][state]==F[i][state] && smaller(s[i],s[u],,)))u=i;
      re(i,,strlen(s[u]+))out[++cnt]=s[u][i];
      for(int T=N-;T;T--)
        {
            int p=-,o,v,cost;
            for(i=first[u],v=edge[i].v,cost=edge[i].cost;i!=-;i=edge[i].next,v=edge[i].v,cost=edge[i].cost)
              if(wei(state,v) && F[v][state-two(u)]+cost==F[u][state])
                if(p==- || smaller(s[v],s[p],cost+,o))
                  p=v,o=cost+;
            re(i,o,strlen(s[p]+))out[++cnt]=s[p][i];
                state-=two(u);
            u=p;
        }
      re(i,,cnt)putchar(out[i]);putchar('\n');
      return ;
  }