FFT算法

FFT算法的完整DSP实现

傅里叶变换或者FFT的理论参考：

[1] http://www.dspguide.com/ch12/2.htm

The Scientist and Engineer's Guide to Digital
Signal Processing,   By Steven W. Smith, Ph.D.

[2] http://blog.csdn.net/v_JULY_v/article/details/6196862，可当作[1]的中文参考

[3] 任意一本数字信号处理教材，上面都有详细的推导DCT求解转换为FFT求解的过程

[4] TI文档：基于TMS320C64x+DSP的FFT实现。 使用baidu/google可以搜索到。

1. 有关FFT理论的一点小小解释

关于FFT这里只想提到两点：

（1）DFT变换对的表达式（必须记住）

 
        —— 称旋转因子

（2）FFT用途——目标只有一个，加速DFT的计算效率。

DFT计算X(k)需要N^2次复数乘法和N(N-1)次复数加法；FFT将N^2的计算量降为。

“FFT其实是很难的东西，即使常年在这个领域下打拼的科学家也未必能很好的写出FFT的算法。”——摘自参考上面提供的参考文献[1]

因此，我们不必太过纠结于细节，当明白FFT理论后，将已有的算法挪过来用就OK了，不必为闭着教材写不出FFT而郁闷不堪。

FFT的BASIC程序伪代码如下：

IFFT的BASIC程序伪代码如下（IFFT通过调用FFT计算）：

FFT算法的流程图如下图，总结为3过程3循环：

（1）3过程：单点时域分解（倒位序过程） + 单点时域计算单点频谱 + 频域合成

（2）3循环：外循环——分解次数，中循环——sub-DFT运算，内循环——2点蝶形算法

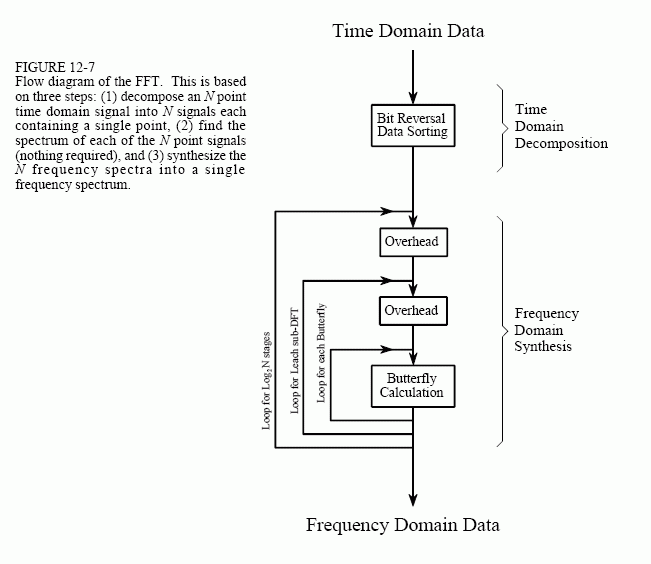
分解过程或者说倒位序的获得参考下图理解：

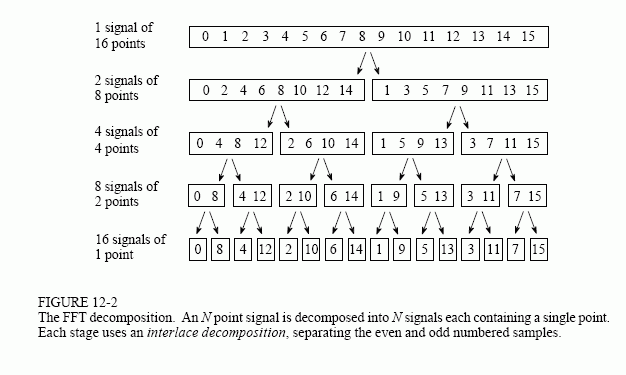
2. FFT的DSP实现

下面为本人使用C语言实现的FFT及IFFT算法实例，能计算任意以2为对数底的采样点数的FFT，算法参考上面给的流程图。

/*
 * zx_fft.h
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */

#ifndef ZX_FFT_H_
#define ZX_FFT_H_

typedef float          FFT_TYPE;

#ifndef PI
#define PI             (3.14159265f)
#endif

typedef struct complex_st {
	FFT_TYPE real;
	FFT_TYPE img;
} complex;

int fft(complex *x, int N);
int ifft(complex *x, int N);
void zx_fft(void);

#endif /* ZX_FFT_H_ */

/*
 * zx_fft.c
 *
 * Implementation of Fast Fourier Transform(FFT)
 * and reversal Fast Fourier Transform(IFFT)
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */

#include "zx_fft.h"
#include <math.h>
#include <stdlib.h>

/*
 * Bit Reverse
 * === Input ===
 * x : complex numbers
 * n : nodes of FFT. @N should be power of 2, that is 2^(*)
 * l : count by bit of binary format, @l=CEIL{log2(n)}
 * === Output ===
 * r : results after reversed.
 * Note: I use a local variable @temp that result @r can be set
 * to @x and won't overlap.
 */
static void BitReverse(complex *x, complex *r, int n, int l)
{
	int i = 0;
	int j = 0;
	short stk = 0;
	static complex *temp = 0;

	temp = (complex *)malloc(sizeof(complex) * n);
	if (!temp) {
		return;
	}

	for(i=0; i<n; i++) {
		stk = 0;
		j = 0;
		do {
			stk |= (i>>(j++)) & 0x01;
			if(j<l)
			{
				stk <<= 1;
			}
		}while(j<l);

		if(stk < n) {             /* 满足倒位序输出 */
			temp[stk] = x[i];
		}
	}
	/* copy @temp to @r */
	for (i=0; i<n; i++) {
		r[i] = temp[i];
	}
	free(temp);
}

/*
 * FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int fft(complex *x, int N)
{
	int i,j,l,ip;
	static int M = 0;
	static int le,le2;
	static FFT_TYPE sR,sI,tR,tI,uR,uI;

	M = (int)(log(N) / log(2));

	/*
	 * bit reversal sorting
	 */
	BitReverse(x,x,N,M);

	/*
	 * For Loops
	 */
	for (l=1; l<=M; l++) {   /* loop for ceil{log2(N)} */
		le = (int)pow(2,l);
		le2 = (int)(le / 2);
		uR = 1;
		uI = 0;
		sR = cos(PI / le2);
		sI = -sin(PI / le2);
		for (j=1; j<=le2; j++) {   /* loop for each sub DFT */
			//jm1 = j - 1;
			for (i=j-1; i<=N-1; i+=le) {  /* loop for each butterfly */
				ip = i + le2;
				tR = x[ip].real * uR - x[ip].img * uI;
				tI = x[ip].real * uI + x[ip].img * uR;
				x[ip].real = x[i].real - tR;
				x[ip].img = x[i].img - tI;
				x[i].real += tR;
				x[i].img += tI;
			}  /* Next i */
			tR = uR;
			uR = tR * sR - uI * sI;
			uI = tR * sI + uI *sR;
		} /* Next j */
	} /* Next l */

	return 0;
}

/*
 * Inverse FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int ifft(complex *x, int N)
{
	int k = 0;

	for (k=0; k<=N-1; k++) {
		x[k].img = -x[k].img;
	}

	fft(x, N);    /* using FFT */

	for (k=0; k<=N-1; k++) {
		x[k].real = x[k].real / N;
		x[k].img = -x[k].img / N;
	}

	return 0;
}

/*
 * Code below is an example of using FFT and IFFT.
 */
#define  SAMPLE_NODES              (128)
complex x[SAMPLE_NODES];
int INPUT[SAMPLE_NODES];
int OUTPUT[SAMPLE_NODES];

static void MakeInput()
{
	int i;

	for ( i=0;i<SAMPLE_NODES;i++ )
	{
		x[i].real = sin(PI*2*i/SAMPLE_NODES);
		x[i].img = 0.0f;
		INPUT[i]=sin(PI*2*i/SAMPLE_NODES)*1024;
	}
}

static void MakeOutput()
{
	int i;

	for ( i=0;i<SAMPLE_NODES;i++ )
	{
		OUTPUT[i] = sqrt(x[i].real*x[i].real + x[i].img*x[i].img)*1024;
	}
}

void zx_fft(void)
{
	MakeInput();

	fft(x,128);
	MakeOutput();

	ifft(x,128);
	MakeOutput();
}

程序在TMS320C6713上实验，主函数中调用zx_fft()函数即可。

FFT的采样点数为128，输入信号的实数域为正弦信号，虚数域为0，数据精度定义FFT_TYPE为float类型，MakeInput和MakeOutput函数分别用于产生输入数据INPUT和输出数据OUTPUT的函数，便于使用CCS 的Graph功能绘制波形图。这里调试时使用CCS
v5中的Tools -> Graph功能得到下面的波形图（怎么用自己琢磨，不会的使用CCS 的Help）。

输入波形

输入信号的频域幅值表示

FFT运算结果

对FFT运算结果逆变换(IFFT)

如何检验运算结果是否正确呢？有几种方法：

（1）使用matlab验证，下面为相同情况的matlab图形验证代码

SAMPLE_NODES = 128;
i = 1:SAMPLE_NODES;
x = sin(pi*2*i / SAMPLE_NODES);

subplot(2,2,1); plot(x);title('Inputs');
axis([0 128 -1 1]);

y = fft(x, SAMPLE_NODES);
subplot(2,2,2); plot(abs(y));title('FFT');
axis([0 128 0 80]);

z = ifft(y, SAMPLE_NODES);
subplot(2,2,3); plot(abs(z));title('IFFT');
axis([0 128 0 1]);

（2）使用IFFT验证：输入信号的FFT获得的信号再IFFT，则的到的信号与原信号相同

可能大家发现输入信号上面的最后IFFT的信号似乎不同，这是因为FFT和IFFT存在精度截断误差（也叫数据截断噪声，意思就是说，我们使用的float数据类型数据位数有限，没法完全保留原始信号的信息）。因此，IFFT之后是复数（数据截断噪声引入了虚数域，只不过值很小），所以在绘图时使用了计算幅值的方法，

C代码中：

OUTPUT[i] = sqrt(x[i].real*x[i].real + x[i].img*x[i].img)*1024;

matlab代码中：

subplot(2,2,3); plot(abs(z));title('IFFT');

所以IFFT的结果将sin函数的负y轴数据翻到了正y轴。另外，在CCS v5的图形中我们将显示信号的幅度放大了1024倍便于观察，而matlab中没有放大。