量子纠错码——Clifford group

Clifford code

Clifford group是什么？

简单的公式来表达，就是 \(Cl_{n}=\left\{U: U P_{n} U^{\dagger} \in P_{n}\right\}\) 。

用语言来描述，就是对一个泡利施加一个U操作，然后还是一个泡利。

首先，所有的泡利都属于\(Cl_n\)，因为泡利矩阵自己相乘还是泡利。

但也有非泡利的矩阵在这里面，比如H也属于clifford，\(HXH=Z\)，$ HZH=X$

另一个例子是 \(S=\sqrt{Z}=\left(\begin{array}{cc}1 & 0 \\ 0 & i\end{array}\right)\)

\(SZS^{\dagger}=ZSS^{\dagger}=Z\)

\(SXS^{\dagger}=iY\)

但是也并非所有的操作都属于\(Cl_n\)，比如T门，\(TZT^{\dagger}=ZTT^{\dagger}=ZS \notin P\)

对于单量子比特来说：\(Cl_1=\langle X,Z,H,S\rangle\)

但是我们不仅只有单比特，对于多比特，他不是简单的\(Cl_1^{\otimes n}\) ，因为多比特有纠缠。

比如\(SWAP_{ij}\) ，将第i个和第j个交换一下，这很明显操作完了还是一个泡利，属于\(Cl_n\)，\(\operatorname{SWAP}_{i j} X_{i} \operatorname{SWAP}_{i j}^{\dagger}=X_{j}\)

除此之外还有CNOT，CNOT对于原来的泡利在受控比特和控制比特上有所不一样，对X和Z的影响也不一样，其效果如下表：

事实上，我们可以用3个CNOT来构建一个SWAP

所以 \(C l_{n}=\langle H_{i},S_{j},CNOT_{i j}\rangle\)

Clifford group可以做什么？

ok，我们已经知道Clifford的定义了，但是我们为什么要定义一个Clifford group呢？他有什么用？

5 qubit code

定义一组对应五比特编码的stabilizer，\(S=\langle Z X X Z I, I Z X X Z, Z I Z X X, X Z I Z X\rangle\)，我们可以很容易的给她加上最后一位变成\(S=\langle Z X X Z I, I Z X X Z, Z I Z X X, X Z I Z X, X X Z I Z\rangle\)，多出来的这个就是前面4个的乘积，所以不会影响到最后的结果。

接下来，我们定义 normalizers of S ，也就是\(N(S)\)。

对于\(N(S)\)，我们只有一个要求，那就是\(N(S)=\left\{p \in P_{n} | p S p^{\dagger}=S\right\}\)。

对于\(p S p^{\dagger}=S\)，我们可以换一种理解方式，即\(pg=gp \forall g \in S\)。

trivial code

我们都知道，编码其实就是将低维的空间映射到高维，那么最为朴实的一种映射就是补零操作，\(V_{S} \in\left\{|0\rangle^{\otimes n-k} \otimes|\Psi\rangle:|\Psi\rangle \in \mathbb{C}^{2^{k}}\right\}\)，这就是一个简单的把k比特映射到n比特空间的一种trival code。

这种编码的stabilizer很简单，\(S=\left\langle Z_{1}, Z_{2} \dots . Z_{n-k}\right\rangle\)，\(Z_i\)的意思是除了第i个比特是Z其他都是I，这个很好理解，因为前面n-k个比特我们都是\(|0\rangle\)，是Z的特征向量。

那这两个编码之间有什么关系吗？

我们可以给出以下声明：

对于任意的stabilizer code，都可以通过unitary的转化和trivial code等价。

而这个unitary就属于我们的Clifford group。

假设我有一组stabilizer \(S\)，以及这个\(S\)对应的子空间\(V_S\)，那么一定存在一个unitary U 使得 \(USU^{\dagger}=\left\langle Z_{1}, Z_{2} \dots . Z_{n-k}\right\rangle\)

这个时候，我们的子空间\(V_{S}\)就变成了\(V_{USU^{\dagger}}\)

后一句话很好理解，原来这个子空间里的向量为\(|\psi\rangle\)，现在这个子空间里的每一个向量就变成了\(U|\psi\rangle\)

\((USU^{\dagger})U|\psi\rangle=US|\psi\rangle=U|\psi\rangle\)

那么前一个为什么会存在这个U呢？

先来论证一下他的可能性，U会改变一些东西，但是有一些不会改变，比如，他不会改变这个的特征值，而正好，他们都是泡利矩阵，特征值都是正负1；又比如，U不会改变他们的对易和反对易，他们正好都是对易的操作。

事实上，对于泡利矩阵来说，只要他们的对易反对易的模式相同，那么我就可以用U对他们进行一个映射。

我们可以换一个视角从向量的角度来看一看这个问题

令\(a,b \in \mathbb{F}^n\)，那么\(v=\left(\begin{array}{l}a \\ b\end{array}\right) \in F^{2 n}\)

任意一个Pauli都可以用v来表示\(X^{a} Z^{b}=\sigma^{\left(\begin{array}{c}a \\ b\end{array}\right)}\)

那么Clifford group在做什么？

$U\sigma^vU{\dagger} \in P_n $

即，其实就是把\(\sigma^{v_1}\)映射成$\sigma^{v_2} $

\(U\sigma^{v}U^{\dagger}=(-1)^{f(v)}\sigma^{g(v)}\)

我们的下一步就是看这里的函数f(v)和g(v)需要满足哪些条件

这里面一个限制就是U变换不会改变操作本来的对易和反对易。

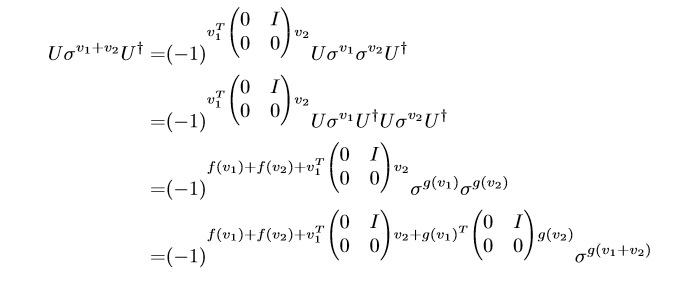
第二个等式是加上了\(U^{\dagger}U\)，因为这两个乘积为\(I\)不会有影响

第三个等式是带入公式\(U\sigma^{v}U^{\dagger}=(-1)^{f(v)}\sigma^{g(v)}\)

如果这里面的\(\sigma^v\)就是我们的\(\sigma^{v_1+v_2}\),那么后面我们的到的就是\((-1)^{f(v_1+v_2)}\sigma^{g(v_1+v_2)}\)

即\(g(v_1+v_2)=g(v_1)+g(v_2)\)，函数g是一个线性函数

g(v)=Mv

但是也不是所有的M是可行的。

\(\sigma^{v} \sigma^{w} \sigma^{v} \sigma^{w}=(-1)^{v^{T}\Lambda w} I\) 其中\(\lambda=\left(\begin{array}{ll}0 & I \\ 0 & 0\end{array}\right)\)

我们可以先把他展开：

\(U \sigma^{N} U^{\dagger}U \sigma^{W} U^{\dagger}U \sigma^{N} U^{\dagger}U\sigma^{W}U=\sigma^{Mv}\sigma^{Mw}\sigma^{Mv}\sigma^{Mw}\)

这里没有系数，因为两个一模一样的系数乘起来就是1，所以系数可以省略掉。

而如果把\(\sigma^{Mw}\sigma^{Mv}\)交换一下可以变成：

\((-1)^{(Mv)^T\Lambda Mw}I\)

我们可以得出：

\(v^T \Lambda w= v^TM^T \Lambda M w\)

即\(\Lambda=M^T \Lambda M\)

而这个就是M需要满足的条件，属于symplectic group。