Computational Geometry

矩形重叠

看过某司一道笔试题：给\(n\)个矩形左下和右上坐标（不能斜放），求重叠最多处矩形个数。

这道题本身不难：可以遍历所有矩形边界组成的点，计算该点被多少矩形包围，从而选出最大值。

由此引申出一个问题：判断两个矩形重叠。

• 如果正向思考，会有很多种情况：包含、重叠某个角、交叉...
  
  那么如果逆向思考：什么情况两个矩形不重叠？无非就是\(A(p_1, p_2)\)在\(B(p_3, p_4)\)的上下左右：

\[(p_2.y>=p_3.y)\vee(p_4.y>=p_1.y)\vee(p_3.x>=p_2.x)\vee(p_1.x>=p_4.x)
\]

取反后用De Morgan's law化简就是重叠的情况：

\[(p_2.y<p_3.y)\wedge(p_4.y<p_1.y)\wedge(p_3.x<p_2.x)\wedge(p_1.x<p_4.x)
\]

线段交点

联立方程组求解当然没问题，也可以用几何的方法解：



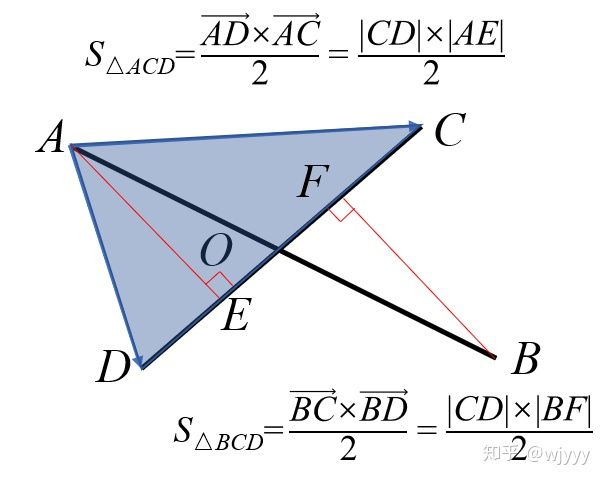
易知，\(\frac{AO}{BO}=\frac{AE}{BF}=\frac{S_{ACD}}{S_{BCD}}\)，两个三角形面积可以用叉积求得，又\(\vec{AO}=\frac{AO}{AB}\vec{AB}=\frac{AO}{AO+BO}\vec{AB}\)，所以\(\vec{O'O}=\vec{O'A}+\vec{AO}\)，即可求得\(O\)点坐标。

向量旋转

三角变换可得：

\[\vec b=(xcos\alpha-ysin\alpha,ycos\alpha+xsin\alpha)
\]

多边形面积

三角剖分：

\[S_{ABCDEF}=\frac{\vec{OA}\times\vec{OB}+\vec{OB}\times\vec{OC}+...+\vec{OF}\times\vec{OA}}{2}
\]

即：

\[S=A_n\times A_1+\sum_{i=1}^{n-1}A_i\times A_{i+1}=x_ny_1-y_nx_1+\sum_{i=1}^{n-1}x_iy_{i+1}-y_ix_{i+1}
\]

凸包

包围所有给定点并且周长最小的多边形。

---

reference

洛谷日报#142 计算几何初步