Johnson-Trotter（JT）算法求全排列

Johnson-Trotter算法描述

算法　　JohnsonTrotter(n)

　　　//实现用来生成排序的 Johnson-Trotter 算法

　　　//输入：正整数n（代表序列1,2，···，n）

　　　//输出：{1,2，···，n}的全排列

　　　将第一个全排列初始化为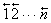

　　　while  存在一个移动元素 do

　　　　求最大的移动元素 k

　　　　把 k 和它箭头指向的相邻元素互换

　　　　调转所有大于 k 的元素的方向

　　　　将新排列添加到排列中

以 n=3 为例

下面我将贴出Johnson-Trotter算法的JAVA代码

 package JT;

 import java.util.Scanner;

 public class Johnson_Trotter {
     //求最大的移动元素
     public static int maxk(int n, int[] array, boolean[] f) {
         //k存储最大移动元素的下标
         int k = -1, max = 0;
         for(int i = 0; i < n; i++) {
             //当前元素的方向是左边，则与左边的元素比较看是否可以移动
             //若可移动则与当前可移动最大值比较
             if(f[i] == false) {
                 if(i > 0 && array[i] > array[i - 1] && array[i] > max) {
                     k = i;
                     max = array[i];
                 }
             }
             //右边
             else {
                 if(i < n - 1 && array[i] >array[i + 1] && array[i] > max) {
                     k = i;
                     max = array[i];
                 }
             }
         }
         return k;
     }
     //元素和方向的交换
     public static int[] swap2(int[] array, boolean[] f, int i, int j) {
         int temp = array[i];
         array[i] = array[j];
         array[j] = temp;
         boolean temp1 = f[i];
         f[i] = f[j];
         f[j] = temp1;
         return array;
     }
     //调转方向
     public static boolean[] Reverseid(int[] array, int k, boolean[] f) {
         for(int i = 0; i < array.length; i++) {
             if(array[i] > array[k]) {
                 f[i] = f[i] ? false : true;
             }
         }
         return f;
     }

     public static void Jt(int n) {
         //方向数组，false为左，true为右
         boolean[] flag = new boolean[n];
         //数字数组
         int[] idata = new int[n];
         //k为当前可移动元素的最大值
         int k = 0;
         //初始化两个数组
         for(int i = 0; i < n; i++) {
             idata[i] = i + 1;
             flag[i] = false;
         }
         //输出第一个初始化的排列，此排列不会自动生成
         for(int i = 0; i < n; i++) {
             System.out.print(idata[i]);
             System.out.print(flag[i]);
         }
         System.out.println();
         //初始化k，获取第一个可移动的最大元素
         k = maxk(n, idata, flag);
         //循环直到没有可移动的元素
         while(k != -1) {
             //可向右移动
             if(flag[k]) {
                 //移动时，将元素和方向都交换
                 idata = swap2(idata, flag, k, k + 1);
                 //此时k所在的元素已经向右交换，k也需要对应加1
                 k++;
             }
             //可向左移动
             else {
                 idata = swap2(idata, flag, k, k - 1);
                 k--;
             }
             flag = Reverseid(idata, k, flag);//调转所有大于k的元素的方向
             //输出当前的一个排列
             for(int i = 0; i < n; i++) {
                 System.out.print(idata[i]);
                 System.out.print(flag[i]);
             }
             System.out.println();
             k = maxk(n, idata, flag);//获取下一个k
         }
     }

     public static void main(String[] args) {
         Scanner scan = new Scanner(System.in);
         int n = scan.nextInt();//输入n
         Jt(n);//调用算法
         scan.close();
     }
 }

代码运行结果如下：(带有元素方向)

Please put in n :4
1false2false3false4false
1false2false4false3false
1false4false2false3false
4false1false2false3false
4true1false3false2false
1false4true3false2false
1false3false4true2false
1false3false2false4true
3false1false2false4false
3false1false4false2false
3false4false1false2false
4false3false1false2false
4true3true2false1false
3true4true2false1false
3true2false4true1false
3true2false1false4true
2false3true1false4false
2false3true4false1false
2false4false3true1false
4false2false3true1false
4true2false1false3true
2false4true1false3true
2false1false4true3true
2false1false3true4true

Process finished with exit code 0

此文章为原创，转载需说明出处。