LeetCode DFS搜索与回溯专题
DFS + 回溯专题
17. 电话号码的字母组合
迭代也可以实现搜索
循环改写dfs搜索的写法:

例如

C++写法
class Solution {
public:
vector<string> letterCombinations(string digits) {
string alp[8] = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> state;
if(digits.empty()) return state;
state.push_back("");
for(int i=0;i<digits.size();i++){
char number = digits[i];
vector<string> now;
for(int j=0;j<alp[number-'2'].size();j++){
char ch = alp[number-'2'][j];
for(int k = 0;k < state.size();k++){
now.push_back(state[k] + ch);
}
}
state = now;
}
return state;
}
};
C++11+ forEach遍历,新语法写法
class Solution {
public:
vector<string> letterCombinations(string digits) {
string alp[8] = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> state;
if(digits.empty()) return state;
state.push_back("");
for(auto digit : digits){ //对digits进行遍历 取得每一个按键数字
vector<string> now;
for(auto c : alp[digit - '2']){ //对数字对应的string能表示的形式遍历
for(auto s : state){ //对state集合里的状态进行遍历
now.push_back(s + c);
}
}
state = now;
}
return state;
}
};
两种写法耗时对比:

79. 单词搜索
搜索题
考虑顺序:
1.枚举起点 n×m
2.从起点开始依次搜索下一个点的位置 上下左右走3种
3.在枚举的过程中要保证和目标单词匹配
时间复杂度 n×m × 3^k,k为单词字符串word的长度
class Solution {
public:
int n,m;
int dx[4] = {1,-1,0,0},dy[4] = {0,0,-1,1}; //上下左右4个方向
bool exist(vector<vector<char>>& board, string word) {
if(board.empty() || board[0].empty()) return false;
n = board.size(),m = board[0].size();
for(int i=0;i<n;i++){ //1.枚举起点(第一个字符向匹配的点)
for(int j=0;j<m;j++){
if(dfs(board,i,j,word,0)) return true; //2.从起点开始搜索
}
}
return false;
}
bool dfs(vector<vector<char>>& board,int x,int y,string word,int k){
if(board[x][y] != word[k]) return false;
//递归出口 当最后一个字符到达
if(k == word.size() - 1) return true;
board[x][y] = '.'; //标记已访问过 用过
for(int i=0;i<4;i++){ //枚举4个方向
int nx = x + dx[i],ny = y + dy[i];
if(nx >= 0 && nx < n && ny >=0 && ny < m){
//递归搜索单词的下一个字符
if(dfs(board,nx,ny,word,k+1)){
return true;
}
}
}
board[x][y] = word[k]; //回溯
return false;
}
};
46. 全排列
全排列,先考虑顺序问题,不能重复
全排列有两种方案
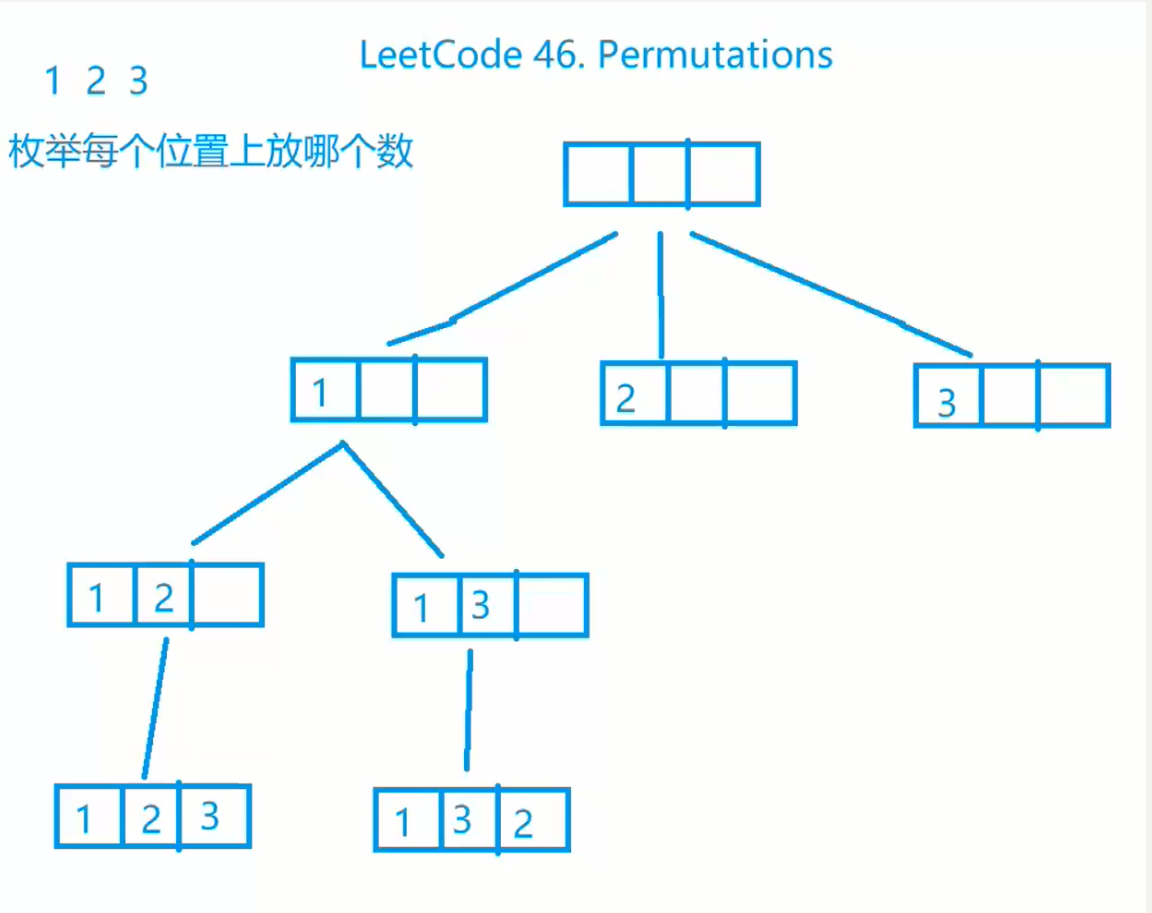

第一种方案,枚举每个位置上放哪个数字,每次dfs搜索时枚举这个数标记、回溯
class Solution {
public:
int n;
vector<bool> vis;
vector<int> path;
vector<vector<int> > result;
vector<vector<int>> permute(vector<int>& nums) {
n = nums.size();
vis = vector<bool>(n,false); //初始化bool容器
dfs(nums,0);
return result;
}
//枚举第k个数该放哪个数字 即枚举数字
void dfs(vector<int>& nums,int k){
if(k == n){
result.push_back(path);
return;
}
//枚举当前第k个位置上该放哪个数字 枚举这个数字的下标
for(int i=0;i<n;i++){
if(!vis[i]){
vis[i] = true; //标记用过
path.push_back(nums[i]); //放入这个数
dfs(nums,k+1);
path.pop_back(); //回溯
vis[i] = false;
}
}
}
};
47. 全排列 II
与leetcode46比较,这题数字可能重复
需要判重
A.采用枚举每个数在哪个位置
B.判重的思路:
1.对nums数组进行排序
2.dfs搜索的时候需要保证值相同的数不在同一个位置上(从下一个位置开始)搜索
class Solution {
public:
int n;
vector<vector<int>> result;
vector<int> path;
vector<bool> visit;
vector<vector<int>> permuteUnique(vector<int>& nums) {
n = nums.size();
visit = vector<bool>(n);
path = vector<int>(n);
sort(nums.begin(),nums.end());
dfs(nums,0,0);
return result;
}
//对一个数枚举该放哪个位置 即枚举位置
void dfs(vector<int>& nums,int k,int start){
if(k == n){ //递归出口
result.push_back(path);
return;
}
//枚举num[k]放的位置在哪
for(int i=start;i<n;i++){ //从start开始枚举
if(!visit[i]){
visit[i] = true;
path[i] = nums[k];
//去重关键:
//对相邻重复元素枚举的位置从下一个位置开始 而不从0开始
if(k+1 <n && nums[k+1] == nums[k]){
dfs(nums,k + 1,i+1);
}else{
dfs(nums,k + 1,0);
}
visit[i] = false;
}
}
}
};
78. 子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
递归考虑顺序:按顺序,枚举每个数两种状态:选、不选
方法一:dfs
class Solution {
public:
int n;
vector<int> path;
vector<vector<int>> result;
vector<vector<int>> subsets(vector<int>& nums) {
n = nums.size();
dfs(0,nums);
return result;
}
void dfs(int k,vector<int>& nums){
if(k == n){
result.push_back(path);
return;
}
dfs(k+1,nums);
path.push_back(nums[k]);
dfs(k+1,nums);
path.pop_back();
}
};
方法2:二进制枚举:i从0到2^n-1,位置上是1的时候选,0的时候不选


class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> result;
//二进制枚举 每个数代表一种方案
for(int i=0;i< 1<<nums.size() ;i++){
vector<int> now;
//枚举每一位 位数一共nums.size()
for(int j=0;j<nums.size();j++){
//如果第j位上数字为1就表示选这个数
if(i >> j & 1){
now.push_back(nums[j]);
}
}
result.push_back(now);
}
return result;
}
};
90. 子集 II
与leetcode78的区别:数字可以重复
枚举的时候,再枚举这个数的选多少个
class Solution {
public:
int n;
vector<vector<int>> result;
vector<int> path;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
n = nums.size();
sort(nums.begin(),nums.end()); //先排序
dfs(nums,0);
return result;
}
void dfs(vector<int>& nums,int k){
if(k == n){
result.push_back(path);
return;
}
//统计后面与当前元素相同的个数
int cnt = 0;
while(k + cnt < n && nums[k + cnt] == nums[k]) cnt++;
for(int i=0;i<=cnt;i++) {
dfs(nums,k + cnt);
path.push_back(nums[k]);
}
for(int i=0;i<=cnt;i++) path.pop_back();
}
};
216. 组合总和 III
找出所有相加之和为 n 的 k个数的组合
组合中只允许含有 1 - 9 的正整数
并且每种组合中不存在重复的数字。

class Solution {
public:
vector<vector<int>> result;
vector<int> path;
vector<vector<int>> combinationSum3(int k, int n) {
dfs(k,1,n);
return result;
}
//当前还剩k个没选 选到了数字start上 总和还需要n
void dfs(int k,int start,int n){
if(k == 0){
if(n == 0) result.push_back(path);
return;
}
for(int i = start; i <= 9; i++ ){
path.push_back(i);
//剩k-1个没选 选到i+1了 总和还需要n-i
dfs(k-1,i+1,n-i);
path.pop_back();
}
}
};
剪枝:因为还需要选k个,i<=9即最大值可以替换为 i<=9 + 1 - k个
for(int i = start; i <= 10-k; i++ )
52. N皇后 II
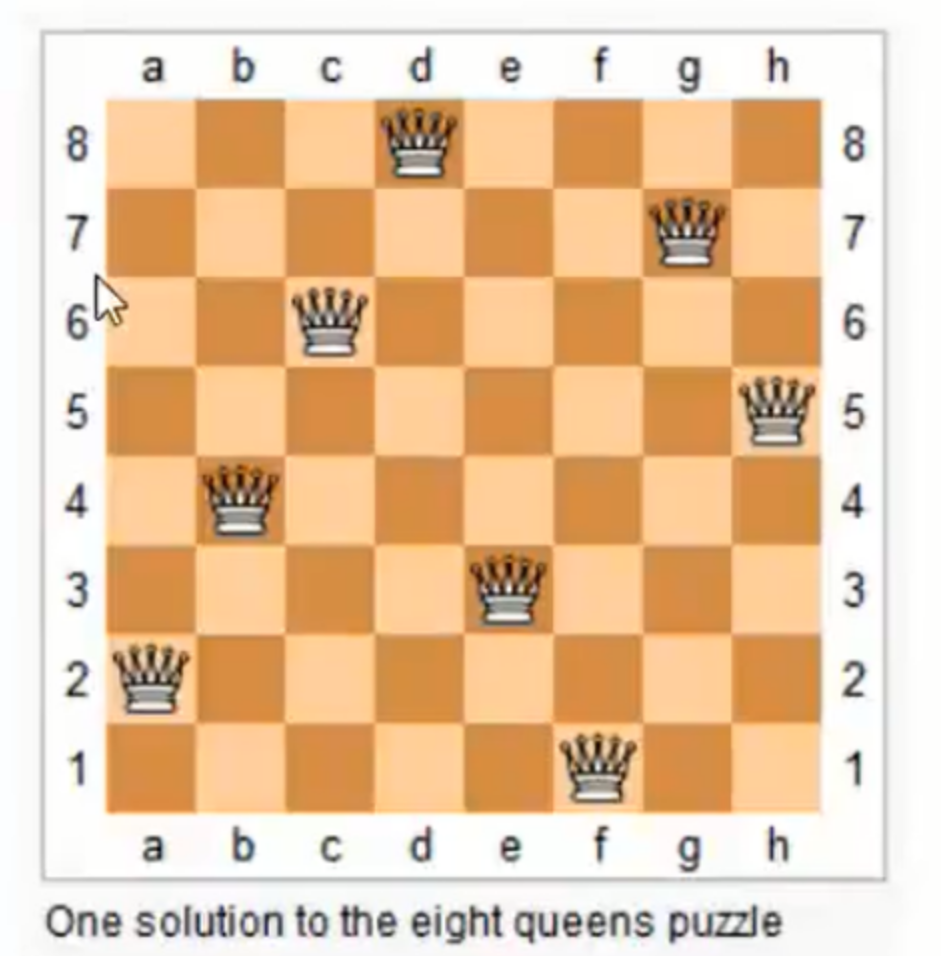
方法一:枚举每一个坐标放不放棋子
class Solution {
public:
int ans;
vector<bool> col,row,diag,anti_diag;
int totalNQueens(int n) {
row = col = vector<bool>(n,false);
diag = anti_diag = vector<bool>(2*n,false);
ans = 0;
dfs(0,0,0,n);
return ans;
}
//当前搜索到的坐标x,y 当前已选择的皇后个数
void dfs(int x,int y,int k,int n){
if(y == n) x++, y = 0;
if(x == n){
if(k == n) ans++;
return;
}
dfs(x,y+1,k,n); //不选这个位置
if(!row[x] && !col[y] && !diag[x+y] && !anti_diag[n+x-y]){
row[x] = col[y] = diag[x+y] = anti_diag[n+x-y] = true;
dfs(x,y+1,k+1,n);
row[x] = col[y] = diag[x+y] = anti_diag[n+x-y] = false;
}
}
};
方法二:枚举每一行放在哪个位置,只需枚举行

37. 解数独

开三个标记数组,分别标记行、列、所在九宫格是否用过某个数
1.先初始化,统计原棋盘已经放的元素。
2.dfs搜索每一个坐标点,枚举该坐标点下能放哪个数字,要求所在行、所在列、所在九宫格都没有这个数字,
3.递归下一个子节点,递归完true就结束程序;否则回溯这个点
52和37的小结:
Dancing Links解决 精确覆盖问题
十字链表
473. 火柴拼正方形
剪枝优化题
超时代码:时间复杂度n^4
class Solution {
public:
int n;
int ave;
vector<bool> vis;
bool makesquare(vector<int>& nums) {
n = nums.size();
vis = vector<bool>(n,false);
sort(nums.begin(),nums.end());
reverse(nums.begin(),nums.end());
long long sum = 0;
int cnt = 0;
for(int i=0;i<n;i++){
sum += nums[i];
}
if(sum == 0 || sum % 4 != 0 ) return false;
for(int i=0;i<n;i++){
if(nums[i] > sum/4) return false;
if(nums[i] == sum/4) {
cnt++;
vis[i] = true;
}
}
if(cnt == 4 && n == 4) return true;
for(int i=0;i<n;i++){
if(nums[i] >= sum/4) continue;
}
ave = sum/4;
return dfs(4-cnt,0,nums);
}
bool dfs(int k,int ans,vector<int>& nums){
if(k == 0){ //递归出口
for(int i=0;i<n;i++){
if(!vis[i]) return false;
}
return true;
}
if(ans > ave) return false; //剪枝
if(ans == ave) return dfs(k-1,0,nums);
//枚举这一轮选的数
for(int i=0;i<n;i++){
if(vis[i]) continue;
vis[i] = true;
if(dfs(k,ans+nums[i],nums)) return true;
vis[i] = false;
}
return false;
}
};

剪枝优化代码:
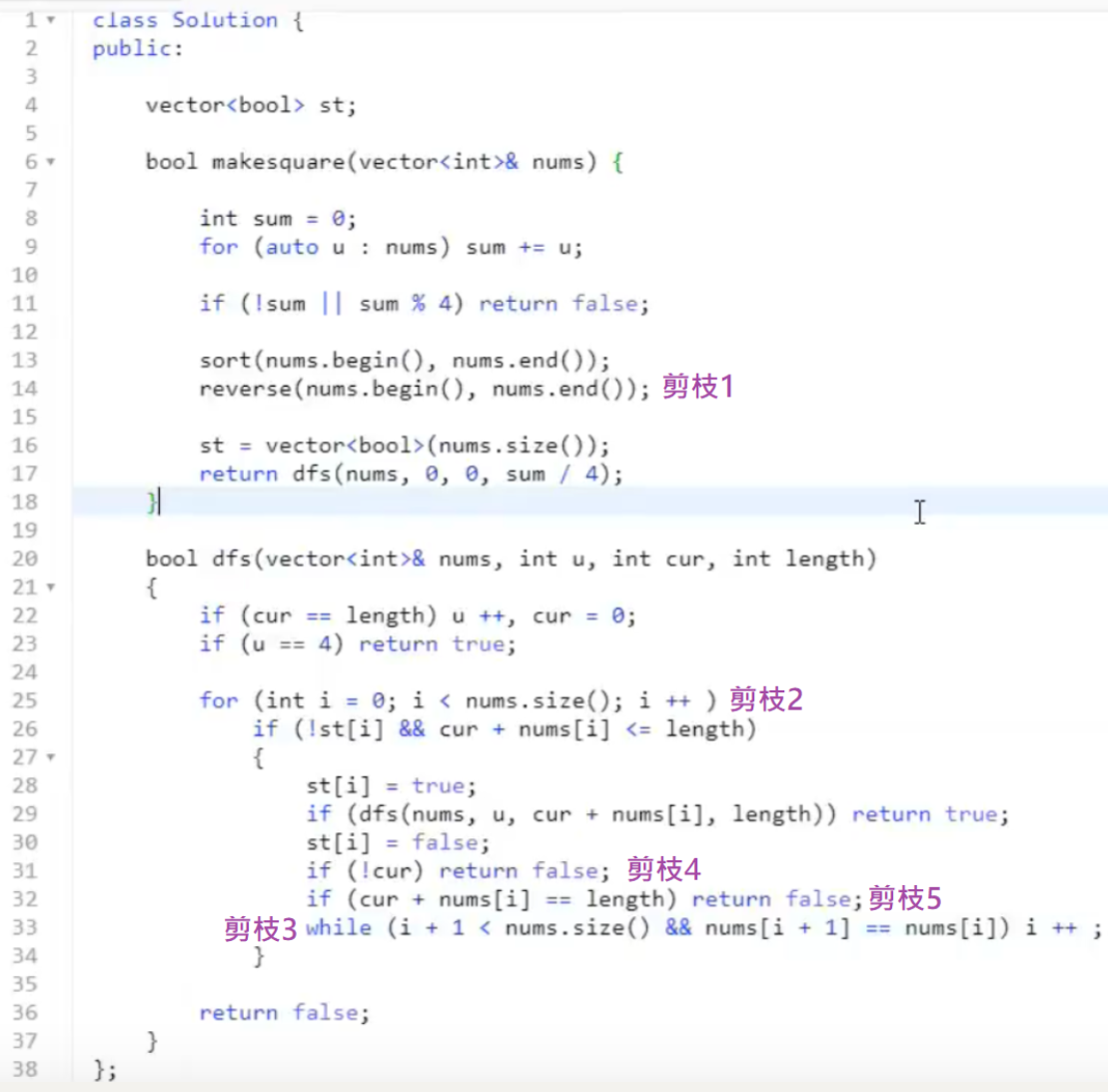
LeetCode DFS搜索与回溯专题的更多相关文章
- Leetcode之深度优先搜索&回溯专题-491. 递增子序列(Increasing Subsequences)
Leetcode之深度优先搜索&回溯专题-491. 递增子序列(Increasing Subsequences) 深度优先搜索的解题详细介绍,点击 给定一个整型数组, 你的任务是找到所有该数组 ...
- Leetcode之深度优先搜索&回溯专题-980. 不同路径 III(Unique Paths III)
Leetcode之深度优先搜索&回溯专题-980. 不同路径 III(Unique Paths III) 深度优先搜索的解题详细介绍,点击 在二维网格 grid 上,有 4 种类型的方格: 1 ...
- Leetcode之深度优先搜索&回溯专题-679. 24 点游戏(24 Game)
Leetcode之深度优先搜索&回溯专题-679. 24 点游戏(24 Game) 深度优先搜索的解题详细介绍,点击 你有 4 张写有 1 到 9 数字的牌.你需要判断是否能通过 *,/,+, ...
- Leetcode之深度优先搜索&回溯专题-638. 大礼包(Shopping Offers)
Leetcode之深度优先搜索&回溯专题-638. 大礼包(Shopping Offers) 深度优先搜索的解题详细介绍,点击 在LeetCode商店中, 有许多在售的物品. 然而,也有一些大 ...
- 蓝桥杯dfs搜索专题
2018激光样式 #include<bits/stdc++.h> using namespace std; /* dfs(i) 第i个激光机器 有两种选择:vis[i-1] == 0 时 ...
- 图解Leetcode组合总和系列——回溯(剪枝优化)+动态规划
Leetcode组合总和系列--回溯(剪枝优化)+动态规划 组合总和 I 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 ...
- nyist oj 19 擅长排列的小明(dfs搜索+STL)
擅长排列的小明 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描写叙述 小明十分聪明.并且十分擅长排列计算.比方给小明一个数字5,他能立马给出1-5按字典序的全排列,假设你想 ...
- hdu 1312:Red and Black(DFS搜索,入门题)
Red and Black Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Tot ...
- [ZOJ 1011] NTA (dfs搜索)
题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=1011 题目大意:在一棵树上,给你起始状态,问你能否到达终止状态. ...
随机推荐
- RMI原理揭秘之远程对象
讨论开始之前,我们先看看网上的一个例子,这个例子我腾抄了一分,没有用链接的方式,只是为了让大家看得方便,如有侵权,我立马***. 定义远程接口: 1 2 3 4 5 6 package com.guo ...
- Jdbc批处理一点异同
同样的代码: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class TestBatch { public stati ...
- CSS3轻松实现彩色旋转六面体动画
一.效果预览: 二.基本思路: 1.首先这个一个自动触发的动画,因此应使用animation设计,包括自动组装和组装完成后自动旋转的过程: 2.当鼠标放上去的时候六个面及上面的字体均变色,应在六个面设 ...
- 对MobileNet网络结构的解读
引言 近几年来,CNN在ImageNet竞赛的表现越来越好.为了追求分类准确度,模型越来越深,复杂度越来越高,如深度残差网络(ResNet)其层数已经多达152层.但是在真实场景中如移动或者嵌入式设备 ...
- python 中open文件路径的选择
一.问题描述 python 中使用open打开某个文件写入时,往往会发现需要写入的文件不在同级目录下.这样就需要根据文件的路径来找到并打开. 但往往有时绝对路径和相对路径,写入不正确就会打开失败. 二 ...
- HDU1176(正推DP)
时间和位置都可以决定这一秒捡到的馅饼数 不妨设\(dp[i][j]\)为在\(i\)秒\(j\)位置的最大收益 那么\(dp[0][5]=0\),dp数组的其他部分置成-1代表不能转移 那么对于第\( ...
- mac安装vue-devtools
mac安装vue devtools 1.到github下载vue tool 的压缩包 正常的方法:git clone https://github.com/vuejs/vue-devtools 但事实 ...
- JavaWebCase
目录 案例:用户登录 用户登录案例需求 分析 开发步骤 创建项目 创建数据库环境 创建包 com.my.domain,创建类User 创建包 com.my.dao,创建类UsesrDao,提供logi ...
- Android自定义顶部栏及侧滑菜单和fragment+viewpag滑动切换的实现
嘿嘿嘿,关于android滑动的操作,是不是经常都会用到呢. 我肯定也要学习一下啦. https://blog.csdn.net/u013184970/article/details/82882107 ...
- 深入理解CSS定位
CSS中有3种定位机制:普通流,浮动和绝对定位.除非专门指定,否则所有框都在普通流中定位.顾名思义,普通流中元素框的位置由HTML元素的位置决定.块级框一个接一个地垂直排列,框之间的垂直距离由框的垂直 ...
