8421BCD转余3码Verilog HDL的设计(1)

　　近期阅读Verilog HDL高级数字设计(第二版)中，遇到了串行比特流BCD码转余3码转换器的设计，比较独特的是：

　　(1)该转换器的输入为1位串行比特流，输出也为1位串行比特流。

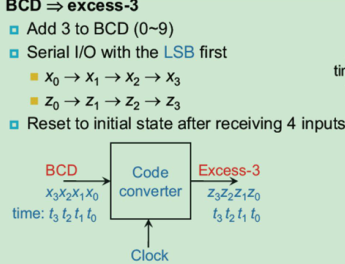
　　BCD码与余三码的转换关系如下：

　　　　　　　　　　　　　　　　　　8421BCD码=余3码+0011

表1 8421BCD码-余3码转换关系(4位无符号数)

10进制	8421BCD码	余3码	10进制	8421BCD码	余3码
0	0000	0011	8	1000	1011
1	0001	0100	9	1001	1100
2	0010	0101	10	1010	1101
3	0011	0110	11	1011	1110
4	0100	0111	12	1100	1111
5	0101	1000	13	1101	10000
6	0110	1001	14	1110	10001
7	0111	1010	15	1111	10010

由表1可知，当8421BCD码为13、14、15时候，余三码已经超出了4位二进制能表示的范围(无符号数0~15)，因此本次中暂不考虑。

转换器的输入为1位串行比特流，输出为1位相应余三码的串行比特流，设计思路如下：

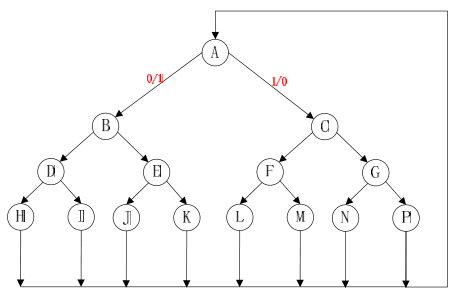
　　　　　　　　　　　　　　　　　　　　　　　　图1 状态转换示意图

　　设BCD码输入比特流Bin在t0,t1,t2,t3的输入分别为t0t1t2t3，设余三码输出比特流Bout在t0,t1,t2,t3时刻的输出分别为T0T1T2T3

假设转换器的初始状态为状态A：

　　(1)在状态A下，t0时刻Bin输入的值可能为0或者1：当bin输入0时，进入B状态；当bin输入1时，进入C状态

比特流Bin二进制为t3t2t1t0的可能性如下：

A状态(t0时刻，Bin=0),Bout=1			A状态(t0时刻，Bin=1)，Bout=0
t3t2t1t0	T3T2T1T0	下一个状态：B	t3t2t1t0	T3T2T1T0	下一个状态：C
0000	0011		0001	0010
0010	0101		0011	0110
0100	0111		0101	1000
0110	1001		0111	1010
1000	1011		1001	1100
1010	1101		1011	1110
1100	1111		1101	(1)0000

　　(2)在B状态，t1时刻Bin输入的值可能为0或者1：当bin输入0时，进入D状态；当bin输入1时，进入E状态

比特流Bin二进制为t3t2t1t0的可能性如下：

B状态(t1时刻，Bin=0),Bout=1			B状态(t1时刻，Bin=1)，Bout=0
t3t2t1t0	T3T2T1T0	下一个状态：D	t3t2t1t0	T3T2T1T0	下一个状态：E
0000	0011		0010	0101
0100	0111		0110	1001
1000	1011		1010	1101
1100	1111		1110	(1)0001

　　(3)在D状态，t2时刻Bin输入的值可能为0或者1：当bin输入0时，进入H状态；当bin输入1时，进入I状态

比特流Bin二进制为t3t2t1t0的可能性如下：

D状态(t2时刻，Bin=0),Bout=0			E状态(t2时刻，Bin=1)，Bout=1
t3t2t1t0	T3T2T1T0	下一个状态：H	t3t2t1t0	T3T2T1T0	下一个状态：I
0000	0011		0100	0111
1000	1011		1100	1111

　　(4)在H状态，t3时刻Bin输入的值可能为0或者1：当bin输入0时，进入A状态；当bin输入1时，进入A状态

比特流Bin二进制为t3t2t1t0的可能性如下：

H状态(t3时刻，Bin=0),Bout=0			H状态(t3时刻，Bin=1)，Bout=1
t3t2t1t0	T3T2T1T0	下一个状态：A	t3t2t1t0	T3T2T1T0	下一个状态：A
0000	0011		1000	1011

　   (5)在I状态，t3时刻Bin输入的值可能为0或者1：当bin输入0时，进入A状态；当bin输入1时，进入A状态

比特流Bin二进制为t3t2t1t0的可能性如下：

I状态(t3时刻，Bin=0),Bout=0			I状态(t3时刻，Bin=1)，Bout=1
t3t2t1t0	T3T2T1T0	下一个状态：A	t3t2t1t0	T3T2T1T0	下一个状态：A
0100	0111		1100	1111

　　(6)在E状态，t2时刻Bin输入的值可能为0或者1：当bin输入0时，进入J状态；当bin输入1时，进入K状态

比特流Bin二进制为t3t2t1t0的可能性如下：

E状态(t2时刻，Bin=0),Bout=1			E状态(t2时刻，Bin=1)，Bout=0
t3t2t1t0	T3T2T1T0	下一个状态:J	t3t2t1t0	T3T2T1T0	下一个状态:K
0010	0101		0110	1001
1010	1101		1110	(1)0001

　　(7)在J状态，t3时刻Bin输入的值可能为0或者1：当bin输入0时，进入A状态；当bin输入1时，进入A状态

比特流Bin二进制为t3t2t1t0的可能性如下：

J状态(t3时刻，Bin=0),Bout=0			J状态(t3时刻，Bin=1)，Bout=1
t3t2t1t0	T3T2T1T0	下一个状态:A	t3t2t1t0	T3T2T1T0	下一个状态:A
0010	0101		1010	1101

　　(8)在K状态，t3时刻Bin输入的值可能为0或者1：当bin输入0时，进入A状态；当bin输入1时，进入A状态

比特流Bin二进制为t3t2t1t0的可能性如下：

K状态(t3时刻，Bin=0),Bout=1			K状态(t3时刻，Bin=1)，Bout=0
t3t2t1t0	T3T2T1T0	下一个状态：A	t3t2t1t0	T3T2T1T0	下一个状态:A
0110	1001		1110	(1)0001

未完待续。。。