BZOJ 4055 Misc

原题传送门

比较复杂的一道DP。

设两点（i，j）之间最短路为dis[i][j]，则

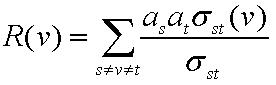
可转化为：

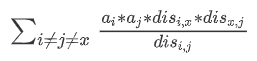
将该式前后分立，可得：

其中，可以单独求出，后面的部分则需要DP。

设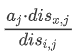为b(x)，枚举i，并计算出从i出发的每个点的dis。

对于每个到达的点k，b(k)可从k相邻的点的b得出。

显然，在枚举过程中可以更新一波答案：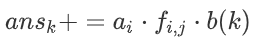

当然，别忘了更新b值：

代码：

 #include <bits/stdc++.h>
 #define sir(i, p) for(sides *i = star[p]; i; i = i -> aftr)
 using namespace std;
 const int N = 1e3 + ;
 int n, m, l, r, a[N], q[N], dis[N], ind[N];
 double pout[N];
 long double bck[N], rnt[N];
 priority_queue <pair <int, int> > queues;
 bool vis[N];
 struct sides {
     int vv, sis;
     sides *aftr;
     long double ends;
 }*star[N], lenss[N << ];
 inline void moree (int x, int y, int z, double w) ;
 void pushups (int x) ;
 void solve (int x) {
     dis[x] = ;
     queues.push (make_pair (, x));
     while (!queues.empty()) {
         int u = queues.top().second;
         queues.pop();
         if (vis[u])
             continue;
         vis[u] = ;
         sir (i, u)
             if (dis[i -> vv] > dis[u] + i -> sis) {
                 dis[i -> vv] = dis[u] + i -> sis;
                 queues.push (make_pair (-dis[i -> vv], i -> vv));
             }
     }
     return ;
 }
 void doit (int x) {
     for (int p = r; p > ; p --) {
         int u = q[p];
         sir (i, u)
             if(dis[i->vv] == dis[u]+i->sis) {
                 int v = i->vv; bck[u] += i->ends*bck[v];
             }
         pout[u] += a[x]*rnt[u]*bck[u];
         bck[u] += (long double)a[u]/rnt[u];
     }
     return ;
 }
 int main() {
     scanf ("%d%d", &n, &m);
     for (int i = ; i <= n; i ++)
         scanf("%d", &a[i]);
     for (int i = ; i <= m; i ++) {
         int x, y, z;
         double w;
         scanf("%d%d%d%lf", &x, &y, &z, &w);
         moree(x, y, z, w);
     }
     for (int i = ; i <= n; i ++) {
         memset (rnt, , sizeof rnt);
         memset (bck, , sizeof bck);
         memset (vis, , sizeof vis);
         memset (dis, 0x3f, sizeof dis);
         solve (i);
         pushups (i);
         doit (i);
     }
     for (int i = ; i <= n; i ++)
         printf ("%.10f\n", pout[i]);
     return ;
 }
 inline void moree (int x, int y, int z, double w) {
     static int _; sides* ls;
     ls = &lenss[++_];
     ls -> vv = y;
     ls -> sis = z;
     ls -> ends = w;
     ls -> aftr = star[x];
     star[x] = ls;
     ls = &lenss[++_];
     ls -> vv = x;
     ls -> sis = z;
     ls -> ends = w;
     ls -> aftr = star[y];
     star[y] = ls;
     return ;
 }
 void pushups (int x) {
     q[r = ] = x;
     l = ;
     rnt[x] = ;
     for (int i = ; i <= n; i ++)
         sir (j, i) {
             if (dis[i] + j -> sis == dis[j -> vv])
                 ind[j -> vv] ++;
         }
     while (r > l) {
         int u = q[++ l];
         sir(i, u)
             if (dis[u] + i -> sis == dis[i -> vv]) {
                 if (!-- ind[i -> vv])
                     q[++r] = i -> vv;
                 rnt[i -> vv] += rnt[u] * i -> ends;
             }
     }
     return ;
 }