Project Euler 94:Almost equilateral triangles 几乎等边的三角形

Almost equilateral triangles

It is easily proved that no equilateral triangle exists with integral length sides and integral area. However, the almost equilateral triangle 5-5-6 has an area of 12 square units.

We shall define an almost equilateral triangle to be a triangle for which two sides are equal and the third differs by no more than one unit.

Find the sum of the perimeters of all almost equilateral triangles with integral side lengths and area and whose perimeters do not exceed one billion (1,000,000,000).

---

几乎等边的三角形

可以证明，不存在边长为整数的等边三角形其面积也是整数。但是，存在几乎等边的三角形 5-5-6，其面积恰好为12。

我们定义几乎等边的三角形是有两条边一样长，且第三边与这两边最多相差1的三角形。

对于周长不超过10亿的三角形中，找出边长和面积都为整数的近似等边三角形的周长和。

解题

这个直接暴力是可以的

先说：几乎等边三角形有两种，边长可以是：a、a、a+1 和a、a、a-1都满足三角形任意两边之和大于第三边，两边之差小于第三边。

下面就是这么根据三边怎么计算面积，并判断面积是整数

我第一想到的是海伦公式

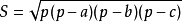
当边长是：a、a、a+1的时候

判断根号下面的平方数，再判断结果S能够被4整除

当边长是：a、a、a-1的时候

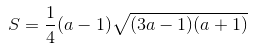
这个和上面也一样了。

这个一个变量时间比较长，表示很伤不起

JAVA

package Level3;

public class PE094{
    public static void run(){
        long MAX = 1000000000;
        long L1 = 0;
        long L2 = 0;
        for(long a =2;;a++){
            if(3*a+1>MAX || 3*a-1>MAX){
                break;
            }
            if(a>=2){
                if(areaIsInteger(a,a+1) == true)
                    L1 +=3*a + 1;
            }
            if(a>=3){
                if(areaIsInteger(a,a-1) == true)
                    L2 +=3*a - 1;
            }
        }

        System.out.println("L1: "+L1);
        System.out.println("L2: "+L2);
        System.out.println(L1 + L2);
    }
//    L1: 109552588
//    L2: 408855758
//    518408346
//    running time=124s662ms
    public static boolean areaIsInteger(long a ,long c){
        // c = a + 1
        if( c == a+1){
            long s1 = (3*a + 1)*(a-1);
            if((long)Math.sqrt(s1) * (long)Math.sqrt(s1) !=s1)
                return false;
            long s2 = (long) ((a+1)*Math.sqrt(s1));
            if(s2%4 != 0)
                return false;
            else{
                return true;
                }
        }
        if( c== a-1){
            long s1 = (3*a -1)*(a+1);
            if((long)Math.sqrt(s1)*(long)Math.sqrt(s1) !=s1)
                return false;
            long s2 = (long)((a-1)*Math.sqrt(s1));
            if(s2%4 != 0)
                return false;
            else{
                return true;
                }
        }
        return true;
    }
    public static void main(String[] args) {
        long t0 = System.currentTimeMillis();
        run();
        long t1 = System.currentTimeMillis();
        long t = t1 - t0;
        System.out.println("running time="+t/1000+"s"+t%1000+"ms");

    }
}

上面根据海伦公式判断面积是否是整数，比较复杂。

直接根据三角形底乘高除以2比较简单点。

公式：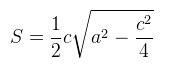

判断面积是否是整数的程序如下

    public static boolean areaIsInteger2(long a,long c){
        if(c*c%4!=0)
            return false;
        long s0 = a*a-c*c/4;
        long sqrt = (long)(Math.sqrt(s0));
        if(sqrt * sqrt != s0)
            return false;
        long s = c*sqrt;
        if(s%2!=0)
            return false;
        return true;
    }

这个比较简单了，运行时间还是比较快的

//    L1: 109552588
//    L2: 408855758
//    518408346
//    running time=48s879ms