实验一：实现求正整数1-N之间所有质数的功能，并进行测试。

实验一 Java开发环境的熟悉(Linux + Eclipse)

实验内容

1.使用JDK编译、运行简单的Java程序；

2.使用Eclipse 编辑、编译、运行、调试Java程序。

• 命令行下的程序开发
• 进入虚拟机终端，mkdir 20155329test cd 20155329test mkdir exp1 cd exp1建立并进入实验一文件夹。
• 编译，运行 Java程序
• 

使用IDEA编辑、编译、运行、调试Java程序

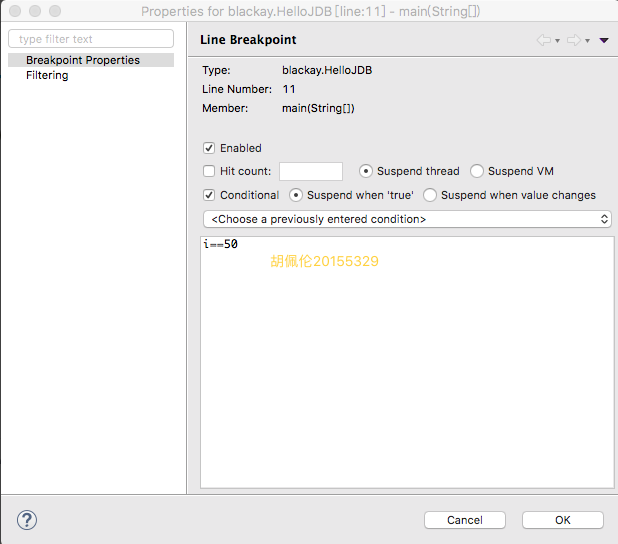
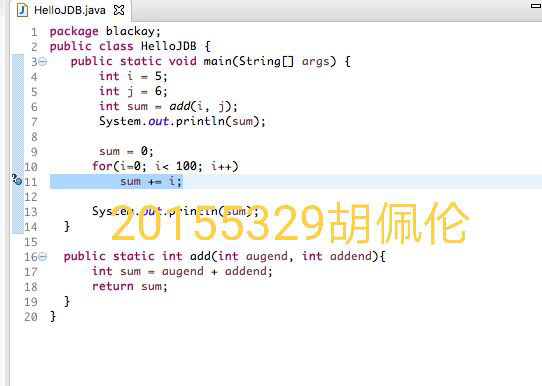
练习（通过命令行和Eclipse两种方式实现，自己的学号后两位与题目总数取余的结果再加上1就是自己要完成的题号，在Eclipse下练习调试程序）

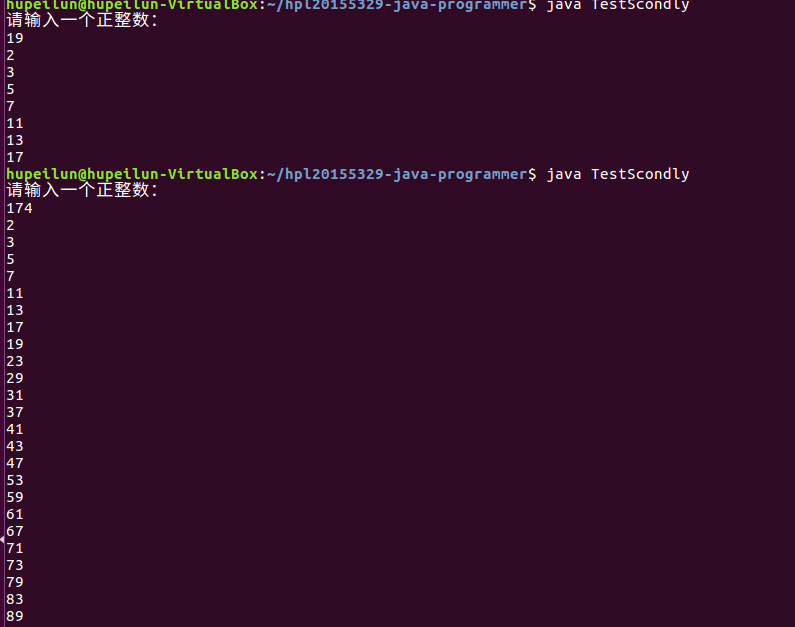
• 实现求正整数1-N之间所有质数的功能，并进行测试。
  
  -代码思路：

• 我的代码：输出0—N之间的所有质数，所以if（N>0）时开始找质数，否则重新输入符合条件的N
  
  -寻找质数：用两个for循环嵌套，相互整除，如果可以整除那么这个数不是质数，如果不能被整除，输出这个数，此数为质数。

import java.io.BufferedReader;

import java.io.IOException;

import java.io.InputStreamReader;

public class Test {

               public static void main(String[] args) throws NumberFormatException, IOException{

                               System.out.println("请输入一个整数");

                               BufferedReader strin=new BufferedReader(new InputStreamReader(System.in));

                               int num=Integer.parseInt(strin.readLine());
                              boolean flag;
                               if(num>0){

                                              for(int i=2;i<=num;i++){

                                                             flag = true;

                                                             for(int j = 2; j <=Math.sqrt(i); j++){

                                                                            if(i % j == 0){

                                                                                            flag = false;

                                                                                            break;

                                                                            }

                                                             }

                                                             if(flag){

                                                                            System.out.println(i);

                                                             }

                                              }

                               }else{

                                              System.out.println("请重新输入！");

                               }

               }

}

-

实验中遇见的问题：

-问题1：本实验中多次出现if for 语句 大括号匹配错误问题。





-认识：在编写代码的过程中一定注意每个括号包括的内容，与之对应的另一半。可以先打{}在中间补充内容可能会更加少犯此类问题。

-问题2：最初版本代码遇见不合法输入时就无法运行。

-解决办法：在实验楼中由于我使用了BufferedReader（）方法，因此 这个方法会可能抛出IOException异常，另外输入格式与期望格式不匹配时还会抛出InputMismatchException异常，所以应添加 try{...}catch (Exception e) {System.out.println(e);} 捕捉异常。

3.实验报告中统计自己的PSP(Personal Software Process)时间：

步骤	耗时	百分比
需求分析	20min	13.3%
设计	20min	13.3%
代码实现	60min	40%
测试	30min	20%
分析总结	20min	13.3%

实验体会：

-本次实验题目在C语言中多次做过，所以思路清晰，很快能拟出流程框图，就差框图转换代码。转换代码是出现问题，怎么动态输入N 呢，出现异常怎么处理此类问题。很简单的问题让我不知所措，当被稍稍提醒之后立马出现，哦原来如此之类的感慨。知识点都学过，但是距离运用还有一段距离，这次实验让我深层次的理解感受到了纸上谈兵都是空，实践才是真道理这句话。