动态规划-House Robber

2018-04-29 20:20:56

House Robber问题是leetcode上经典的系列题，这里对其中的题目做一个讲解。

• 198. House Robber

问题描述：

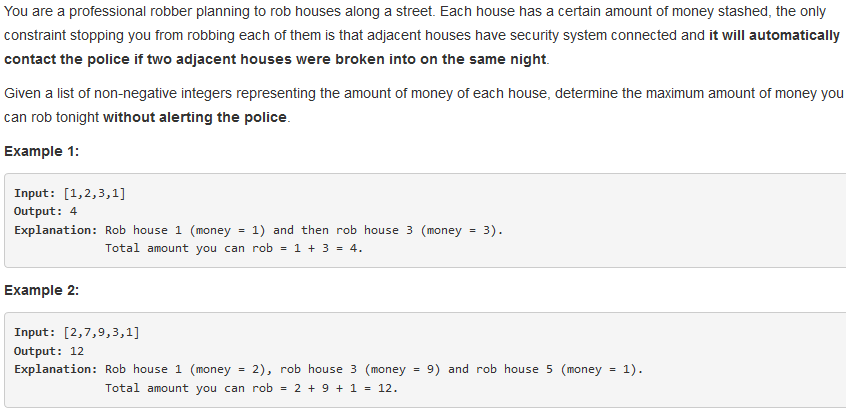
问题求解：

本质上就是求解不连续取数的情况下能获得最大价值。可以使用动态规划来解决。

dp[i][0]：第i个数没有取能获得的最高价值

dp[i][1]：第i个数取能获得的最高价值

初始值：dp[-1][0] = 0，dp[-1][1] = -INF

递推关系式：dp[i][0] = max(dp[i - 1][0]， dp[i - 1][1])

　　　　　   dp[i][1] = dp[i - 1] + nums[i]

    public int rob(int[] nums) {
        int[][] dp = new int[nums.length + 1][2];
        dp[0][0] = 0;
        dp[0][1] = Integer.MIN_VALUE;
        for (int i = 1; i <= nums.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][1], dp[i - 1][0]);
            dp[i][1] = dp[i - 1][0] + nums[i - 1];
        }
        return Math.max(dp[nums.length][0], dp[nums.length][1]);
    }

可以对空间复杂度进行优化：

    public int rob(int[] nums) {
        int dp0 = 0;
        int dp1 = Integer.MIN_VALUE;
        for (int i = 1; i <= nums.length; i++) {
            int tmp = dp0;
            dp0 = Math.max(dp1, dp0);
            dp1 = tmp + nums[i - 1];
        }
        return Math.max(dp0, dp1);
    }

• 213. House Robber II

问题描述：

问题求解：

相较于上一题，本题出现了环路，显然的是如果状态是环路的话是无法运用dp的，因为dp是只考虑目前的情况，无后效性，而环路则意味着后面的状态会影响前面的状态，因此，我们要解决这个问题，首先要做的就是考虑使用某种手段来将环路打开。

对于rob问题，如果第i间屋子没有偷窃的话，那么第i + 1间屋子就可以任意取，也就是对于i + 1间屋子来说第i间屋子和不存在是一样的，因此我们可以在没有被偷窃的屋子上将环路断开。

下面考虑第n间屋子，他有两个状态，一是被偷窃，则第 n + 1间屋子必然没有被偷，则从 n + 1 处断开；二是没有被偷，则直接在 n 处断开。

    public int rob(int[] nums) {
        if (nums.length == 1) return nums[0];
        return Math.max(helper(nums, 0, nums.length - 2), helper(nums, 1, nums.length - 1));
    }

    private int helper(int[] nums, int l, int r) {
        int dp0 = 0;
        int dp1 = Integer.MIN_VALUE;
        for (int i = l; i <= r; i++) {
            int tmp = dp0;
            dp0 = Math.max(dp0, dp1);
            dp1 = tmp + nums[i];
        }
        return Math.max(dp0, dp1);
    }

• 337. House Robber III

问题描述：

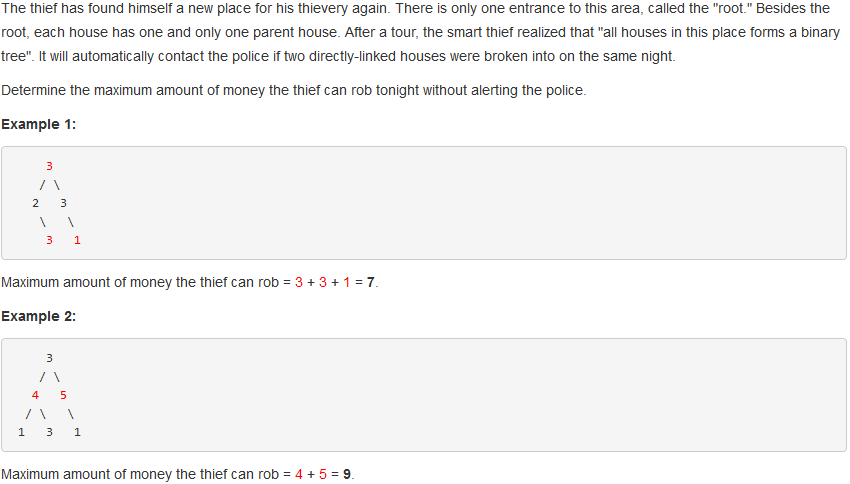
问题求解：

本题是从数据结构的角度对原问题进行了扩展，将场景变到了二叉树上，限制条件依然是不能连续偷取。

从本质上来说，每个结点依然是两个状态，一是偷取了，二是没有偷取，因此，我们依然可以使用动态规划的方法自低向上的将每个结点的左右儿子结点的状态都得到后，再计算自己的值。

    public int rob(TreeNode root) {
        int[] res = helper(root);
        return Math.max(res[0], res[1]);
    }

    private int[] helper(TreeNode root) {
        if (root == null) return new int[2];

        int[] res = new int[2];
        int[] L = helper(root.left);
        int[] R = helper(root.right);

        res[0] = Math.max(L[0], L[1]) + Math.max(R[0], R[1]);
        res[1] = L[0] + R[0] + root.val;
        return res;
    }