poj1821 Fence【队列优化线性DP】

Fence

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 6122		Accepted: 1972

Description

A team of k (1 <= K <= 100) workers should paint a fence which contains N (1 <= N <= 16 000) planks numbered from 1 to N from left to right. Each worker i (1 <= i <= K) should sit in front of the plank Si and he may paint only a compact interval (this means that the planks from the interval should be consecutive). This interval should contain the Si plank. Also a worker should not paint more than Li planks and for each painted plank he should receive Pi $ (1 <= Pi <= 10 000). A plank should be painted by no more than one worker. All the numbers Si should be distinct.

Being the team's leader you want to determine for each worker the interval that he should paint, knowing that the total income should be maximal. The total income represents the sum of the workers personal income.

Write a program that determines the total maximal income obtained by the K workers.

Input

The input contains: 
Input

N K 
L1 P1 S1 
L2 P2 S2 
... 
LK PK SK

Semnification

N -the number of the planks; K ? the number of the workers 
Li -the maximal number of planks that can be painted by worker i 
Pi -the sum received by worker i for a painted plank 
Si -the plank in front of which sits the worker i 

Output

The output contains a single integer, the total maximal income.

Sample Input

8 4
3 2 2
3 2 3
3 3 5
1 1 7

Sample Output

17

Hint

Explanation of the sample:

the worker 1 paints the interval [1, 2];

the worker 2 paints the interval [3, 4];

the worker 3 paints the interval [5, 7];

the worker 4 does not paint any plank

Source

Romania OI 2002

 

题意：

k个工人粉刷n道墙，每个工人最多刷L[i]面，并且必须刷第S[i]面，每刷一面可以拿到P[i]的报酬。一面墙至多只能被刷一次。

思路：

首先我们按照每个工人的S进行排序，就可以保证所有工人可以做到在上一个工人之后粉刷。

用dp[i][j]来表示前i个工人粉刷前j面墙最多所得报酬。

对于一个工人i，他可以刷也可以不刷。对于一面墙j，他可以被刷也可以不被刷。

所以dp[i][j] = max(dp[i -1][j], dp[i][j -1])

dp[i][j] 的第三种情况是第i个工人从第k+1块刷到第j块。 k+1 <= Si <= j, j - k<= Li

可以得到状态转移方程：

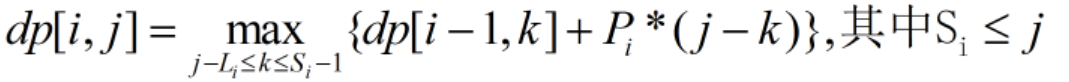
当我们循环j，k时，可以把i看成是定值，于是对于这条方程我们可以进行一定的变形，将j和k分离。

 

当j增大时，k的取值上界不变，下界增大。

如果现在有两个决策k1,k2. 且k1 < k2 <=Si-1，如果还满足dp[i-1,k1] - Pi * k1<= dp[i -1, k2] - Pi * k2

那么k2不但比k1更优，存活时间也更长，此时k1就是一个无用决策。

所以可以维护一个决策点k单调递增，dp[i-1,k] - Pi * k单调递减的队列。

当 j 变大时，检查队头，将小于j-Li的决策出队

查询最优决策时，队头即为所求。

当有一个新的决策需要入队时，检查队尾单调性，把无用决策出队，最后新决策入队。

 

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <map>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f

 int k, n;
 struct node{
     int l, s, p;
 }worker[];
 int que[], dp[][];
 bool cmp(node a, node b)
 {
     return a.s < b.s;
 }

 int cal(int i, int k)
 {
     return dp[i - ][k] - worker[i].p * k;
 }

 int main()
 {
     //freopen("in.txt", "r", stdin);
     //freopen("out.txt", "w", stdout);
     while(scanf("%d%d", &n, &k)!= EOF){
         for(int i = ; i <= k; i++){
             scanf("%d%d%d", &worker[i].l, &worker[i].p, &worker[i].s);
             //printf("%d%d%d\n", worker[i].l, worker[i].s, worker[i].p);
         }
         sort(worker + , worker +  + k, cmp);

         /*for(int i = 1; i <= k; i++){
             printf("%d%d%d\n", worker[i].l, worker[i].s, worker[i].p);
         }*/
         for(int i = ; i <= k; i++){
             int l = , r = ;
             for(int x = max(, worker[i].s - worker[i].l); x <= worker[i].s - ; x++){
                 while(l <= r && cal(i, que[r]) <= cal(i, x)){
                     r--;
                 }
                 que[++r] = x;
             }
             for(int j = ; j <= n; j++){
                 dp[i][j] = max(dp[i - ][j], dp[i][j - ]);
                 if(j >= worker[i].s){
                     while(l <= r && que[l] < j - worker[i].l)l++;
                     if(l <= r){
                         dp[i][j] = max(dp[i][j], cal(i, que[l]) + worker[i].p * j);
                     }
                     //cout<<dp[i][j]<<endl;
                 }
             }
         }

         //int ans = 0;
         //for(int i = 1; i <= n; i++){
         //    ans = max(ans, dp[k][i]);
         //}
         printf("%d\n", dp[k][n]);
     }
 }