C#排序算法小结

前言

算法这个东西其实在开发中很少用到，特别是web开发中，但是算法也很重要，因为任何的程序，任何的软件，都是由很多的算法和数据结构组成的。但是这不意味着算法对于每个软件设计人员的实际工作都是很重要的。每个项目特点和需求特殊也导致算法运用场景上不同。但是个人觉得算法运用的好的话会给自己在程序设计的时候提供比较好的思路。下面就对一些排序算法小结一下，就当做自己的一个笔记吧。

插入排序

 1.简介

插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

2.算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：
1.从第一个元素开始，该元素可以认为已经被排序
2.取出下一个元素，在已经排序的元素序列中从后向前扫描
3.如果该元素（已排序）大于新元素，将该元素移到下一位置
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5.将新元素插入到该位置后
6.重复步骤2~5
如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找排序。

3.使用插入排序为一列数字进行排序的过程

 

 

最差时间复杂度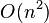

最优时间复杂度

平均时间复杂度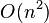

4.C#实现

        /// <summary>
        /// 插入排序
        /// </summary>
        public class InsertionSorter
        {
            public void Sort(int[] list)
            {
                for (int i = ; i < list.Length; ++i)
                {
                    int t = list[i];
                    int j = i;
                    while ((j > ) && (list[j - ] > t))
                    {
                        list[j] = list[j - ];
                        --j;
                    }
                    list[j] = t;
                }
 
            }
        }

数组

int[] iArrary = new int[] { , , , , , , , , , , , , ,  };

希尔排序

 1.简介

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

2.算法实现

原始的算法实现在最坏的情况下需要进行O(n2)的比较和交换。V. Pratt的书[1] 对算法进行了少量修改，可以使得性能提升至O(n log2 n)。这比最好的比较算法的O(n log n)要差一些。
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序（冒泡排序或插入排序），可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。
一个更好理解的希尔排序实现：将数组列在一个表中并对列排序（用插入排序）。重复这过程，不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身仅仅对原数组进行排序（通过增加索引的步长，例如是用i += step_size而不是i++）。

3.排序过程

 

最差时间复杂度 根据步长串行的不同而不同。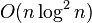

最优时间复杂度 O(n)

平均时间复杂度  根据步长串行的不同而不同。

4.C#实现

        /// <summary>
        /// 希尔排序
        /// </summary>
        public class ShellSorter
        {
            public void Sort(int[] list)
            {
                int inc;
                for (inc = ; inc <= list.Length / ; inc =  * inc + ) ;
                for (; inc > ; inc /= )
                {
                    for (int i = inc + ; i <= list.Length; i += inc)
                    {
                        int t = list[i - ];
                        int j = i;
                        while ((j > inc) && (list[j - inc - ] > t))
                        {
                            list[j - ] = list[j - inc - ];
                            j -= inc;
                        }
                        list[j - ] = t;
                    }
                }
            }
        }

选择排序

1.简介

选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

2.实现过程

 

最差时间复杂度 О(n²)

最优时间复杂度 О(n²)

平均时间复杂度 О(n²)

3.C#实现

        /// <summary>
        /// 选择排序
        /// </summary>
        public class SelectionSorter
        {
            // public enum comp {COMP_LESS,COMP_EQUAL,COMP_GRTR};
            private int min;
            // private int m=0;
            public void Sort(int[] list)
            {
                for (int i = ; i < list.Length - ; ++i)
                {
                    min = i;
                    for (int j = i + ; j < list.Length; ++j)
                    {
                        if (list[j] < list[min])
                            min = j;
                    }
                    int t = list[min];
                    list[min] = list[i];
                    list[i] = t;
                    // Console.WriteLine("{0}",list[i]);
                }
 
            }
        }

冒泡排序

 1.简介

冒泡排序（Bubble Sort，台湾译为：泡沫排序或气泡排序）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序对n个项目需要O(n^{2})的比较次数，且可以原地排序。尽管这个算法是最简单了解和实作的排序算法之一，但它对于少数元素之外的数列排序是很没有效率的。
冒泡排序是与插入排序拥有相等的执行时间，但是两种法在需要的交换次数却很大地不同。在最坏的情况，冒泡排序需要O(n^{2})次交换，而插入排序只要最多O(n)交换。冒泡排序的实现（类似下面）通常会对已经排序好的数列拙劣地执行（O(n^{2})），而插入排序在这个例子只需要O(n)个运算。因此很多现代的算法教科书避免使用冒泡排序，而用插入排序取代之。冒泡排序如果能在内部循环第一次执行时，使用一个旗标来表示有无需要交换的可能，也有可能把最好的复杂度降低到O(n)。在这个情况，在已经排序好的数列就无交换的需要。若在每次走访数列时，把走访顺序和比较大小反过来，也可以稍微地改进效率。有时候称为往返排序，因为算法会从数列的一端到另一端之间穿梭往返。

2.算法实现
1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3.针对所有的元素重复以上的步骤，除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

3.实现过程

 

最差时间复杂度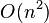

最优时间复杂度

平均时间复杂度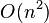

4.C#实现

       /// <summary>
        /// 冒泡排序
        /// </summary>
        public class bubblesort
        {
            public void BubbleSort(int[] R)
            {
                int i, j, temp; //交换标志
                bool exchange;
                for (i = ; i < R.Length; i++) //最多做R.Length-1趟排序
                {
                    exchange = false; //本趟排序开始前，交换标志应为假
                    for (j = R.Length - ; j >= i; j--)
                    {
                        if (R[j + ] < R[j])　//交换条件
                        {
                            temp = R[j + ];
                            R[j + ] = R[j];
                            R[j] = temp;
                            exchange = true; //发生了交换，故将交换标志置为真
                        }
                    }
                    if (!exchange) //本趟排序未发生交换，提前终止算法
                    {
                        break;
                    }
                }
            }
        }