Amphetamine的cf日记

之前挂上的

今天填坑

2018.2.14 #462

A

给两个集合，B分别可以从一个集合中选一个数，B想乘积最大，A想最小，A可以删除一个第一个集合中的元素，问最小能达到多少。

这题。。水死啦。我居然还wa了一发，因为ans初值定的0.。。。。我真是傻。

n3暴力就行

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inf 1000000000000000001ll
int n,m;
ll a[],b[];
ll ans=inf;
int main(){
    cin>>n>>m;
    for(int i=;i<=n;i++)cin>>a[i];
    for(int i=;i<=m;i++)cin>>b[i];
    for(int k=;k<=n;k++){
    ll ret=-inf;
    for(int i=;i<=n;i++){
        if(i==k)continue;
        for(int j=;j<=m;j++){
            ret=max(ret,a[i]*b[j]);
        }
    }
    ans=min(ans,ret);
    }
    cout<<ans<<endl;
    return ;
} 

B

我记得小时候的脑筋急转弯

6666=4

8888=8

1234=1

5678=?

哈哈

数圈嘛

先全输出8，剩一个就输出6，剩下的输出1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int k;

int main(){
    cin>>k;
    if(k>){
        cout<<-<<endl;
        return ;
    }
    else {
        for(int i=;i<=;i++){
            if(k>=){
                cout<<;
                k-=;
            }
            else if(k==){
            cout<<;k--;}
            else cout<<;
        }
    }
    return ;
} 

C

一个只有1，2的序列，你可以翻转一次任意子串，问翻转之后最长不下降子序列。

选择很多？？？

这题随便做嘛。

我是利用了一个小性质，就是从1到2的分界点，一定是在翻转的区间里，否则没意义。

然后枚举翻转区间，维护一下最长不下降子序列就好了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int a[];
int l1[],l2[],r1[],r2[];
int n;
int ans;
int main(){
    cin>>n;
    for(int i=;i<=n;i++)cin>>a[i];
    for(int i=;i<=n;i++){
        l1[i]=l1[i-];
        l2[i]=l2[i-];
        if(a[i]==)l1[i]++;
        else l2[i]++;
    }
    for(int i=n;i>=;i--){
        r1[i]=r1[i+];
        r2[i]=r2[i+];
        if(a[i]==)r1[i]++;
        else r2[i]++;
    }
    for(int i=;i<=n+;i++){
        ans=max(ans,l1[i-]+r2[i]);
        int ret=l1[i-]+r2[i];
        int j=i-;
        while(j&&a[j]==)j--;
        int tt=;
        for(;j>;j--){
            if(a[j]==)tt++;
            else if(tt)tt--;
            ans=max(ans,ret+tt);
        }
    }
    cout<<ans<<endl;
    return ;
} 

D

好题！！！

n order to put away old things and welcome a fresh new year, a thorough cleaning of the house is a must.

Little Tommy finds an old polynomial and cleaned it up by taking it modulo another. But now he regrets doing this...

Given two integers p and k, find a polynomial f(x) with non-negative integer coefficients strictly less than k, whose remainder is p when divided by (x + k). That is, f(x) = q(x)·(x + k) + p, where q(x) is a polynomial (not necessarily with integer coefficients).

Input

The only line of input contains two space-separated integers p and k (1 ≤ p ≤ 1018, 2 ≤ k ≤ 2 000).

Output

If the polynomial does not exist, print a single integer -1, or output two lines otherwise.

In the first line print a non-negative integer d — the number of coefficients in the polynomial.

In the second line print d space-separated integers a0, a1, ..., ad - 1, describing a polynomial 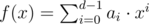 fulfilling the given requirements. Your output should satisfy 0 ≤ ai < k for all 0 ≤ i ≤ d - 1, and ad - 1 ≠ 0.

If there are many possible solutions, print any of them.

这题没有special judge

只有唯一解

根据多项式意义，可以发现，f(x)的第一位是可以立即确定的，然后根据第一位可以推出第二位....依次类推。

然后我们发现，这个不断从上一项推出下一项的过程，很像之前做过的负进制转换。（luoguP 1107）

吐槽一下，我当时发现很像，并且过了pretest之后，告诉洛谷群，结果群里面一堆小孩说我钓鱼。。。。。

这件事情教育我们，干什么要先过脑子，，，，，

其实就是把p转化为（-k）进制，输出，结束。

(自行去luogu题解粘代码)

E

计算几何，，，，，gg

#include<bits/stdc++.h>
using namespace std;
struct point{
    double x,y;
};
double xmult(point p1,point p2,point p0){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double dist(point p1,point p2){
    return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}  

point intersection(point u1,point u2,point v1,point v2){
    point ret=u1;
    double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))
            /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
    ret.x+=(u2.x-u1.x)*t;
    ret.y+=(u2.y-u1.y)*t;
    return ret;
}
const double eps=1e-;
point dot_to_circle(point c,double r,point p){
    point u,v;
    if (dist(p,c)<eps)
        return p;
    u.x=c.x+r*fabs(c.x-p.x)/dist(c,p);
    u.y=c.y+r*fabs(c.y-p.y)/dist(c,p)*((c.x-p.x)*(c.y-p.y)<?-:);
    v.x=c.x-r*fabs(c.x-p.x)/dist(c,p);
    v.y=c.y-r*fabs(c.y-p.y)/dist(c,p)*((c.x-p.x)*(c.y-p.y)<?-:);
    return dist(u,p)<dist(v,p)?u:v;
}
void intersection_line_circle(point c,double r,point l1,point l2,point& p1,point& p2){
    point p=c;
    double t;
    p.x+=l1.y-l2.y;
    p.y+=l2.x-l1.x;
    p=intersection(p,c,l1,l2);
    t=sqrt(r*r-dist(p,c)*dist(p,c))/dist(l1,l2);
    p1.x=p.x+(l2.x-l1.x)*t;
    p1.y=p.y+(l2.y-l1.y)*t;
    p2.x=p.x-(l2.x-l1.x)*t;
    p2.y=p.y-(l2.y-l1.y)*t;
}
void intersection_circle_circle(point c1,double r1,point c2,double r2,point& p1,point& p2){
    point u,v;
    double t;
    t=(+(r1*r1-r2*r2)/dist(c1,c2)/dist(c1,c2))/;
    u.x=c1.x+(c2.x-c1.x)*t;
    u.y=c1.y+(c2.y-c1.y)*t;
    v.x=u.x+c1.y-c2.y;
    v.y=u.y-c1.x+c2.x;
    intersection_line_circle(c1,r1,u,v,p1,p2);
}  

int n;
int sqr(int x){
    return x*x;
}
int cross(int a,int b,int c,int d,int e,int f){
    if(sqr(a-d)+sqr(b-e)>=sqr(c+f))return ;
    if(sqr(a-d)+sqr(b-e)<=sqr(c-f))return ;
    return ;
}
int a,b,c,d,e,f,g,h,i;
int ct(int a,int b,int c,int d,int e,int f){
    if(sqr(a-d)+sqr(b-e)==sqr(c+f))return ;
    if(sqr(a-d)+sqr(b-e)==sqr(c-f))return ;
    return ;
}
//3
//-4 4 4
//2 4 2
//-1 0 6

int main()
{
    cin>>n;
    if(n==){
        cin>>a>>b>>c;
        cout<<;
        return ;
    }
    if(n==){
        cin>>a>>b>>c>>d>>e>>f;
        cout<<+cross(a,b,c,d,e,f);
        return ;
    }
    cin>>a>>b>>c>>d>>e>>f>>g>>h>>i;
    int ret=;
    if(cross(a,b,c,d,e,f)&&cross(d,e,f,g,h,i)&&cross(g,h,i,a,b,c)){
    ret=;
    double num1,num2,num3,num4,num5,num6;
    double r1,r2,r3;
    num1=a,num2=b,r1=c;
    num3=d,num4=e,r2=f;
    num5=g,num6=h,r3=i;
    point w,ww,p1,p2;
    w.x=a,w.y=b;ww.x=d,ww.y=e;
    intersection_circle_circle(w,r1,ww,r2,p1,p2);
    num1=p1.x,num2=p1.y,num3=p2.x,num4=p2.y;
    if(fabs((num1-num5)*(num1-num5)+(num2-num6)*(num2-num6)-r3*r3)<eps)ret--;
    if(fabs((num3-num5)*(num3-num5)+(num4-num6)*(num4-num6)-r3*r3)<eps)ret--;
    cout<<ret<<endl;
    }
    else {
        ret=+cross(a,b,c,d,e,f)+cross(d,e,f,g,h,i)+cross(g,h,i,a,b,c);
        if(ret==){
            if((ct(a,b,c,d,e,f)+)/+(ct(d,e,f,g,h,i)+)/+(ct(g,h,i,a,b,c)+)/){
                double num1,num2,num3,num4,num5,num6;
    double r1,r2,r3;
    num1=a,num2=b,r1=c;
    num3=d,num4=e,r2=f;

                if(cross(a,b,c,d,e,f)){
                    point w,ww,p1,p2;
                    w.x=a,w.y=b;ww.x=d,ww.y=e;
                    intersection_circle_circle(w,r1,ww,r2,p1,p2);
                    num1=p1.x,num2=p1.y,num3=p2.x,num4=p2.y;
                    num5=g,num6=h,r3=i;if(fabs((num1-num5)*(num1-num5)+(num2-num6)*(num2-num6)-r3*r3)>eps&&fabs((num3-num5)*(num3-num5)+(num4-num6)*(num4-num6)-r3*r3)>eps)ret++;
                }
                else if(cross(a,b,c,g,h,i)){point w,ww,p1,p2;
                    w.x=a,w.y=b;ww.x=g,ww.y=h;
                    intersection_circle_circle(w,r1,ww,i,p1,p2);
                    num1=p1.x,num2=p1.y,num3=p2.x,num4=p2.y;
                    num5=d,num6=e,r3=f;if(fabs((num1-num5)*(num1-num5)+(num2-num6)*(num2-num6)-r3*r3)>eps&&fabs((num3-num5)*(num3-num5)+(num4-num6)*(num4-num6)-r3*r3)>eps)ret++;
                }
            }
        }
        else if(ret==){
            ret+=((ct(a,b,c,d,e,f)+)/+(ct(d,e,f,g,h,i)+)/+(ct(g,h,i,a,b,c)+)/)/;
        }
        if(ret==){
            if(ct(a,b,c,d,e,f)&&ct(d,e,f,g,h,i)&&ct(g,h,i,a,b,c)){
                double num1,num2,num3,num4;
                if(ct(a,b,c,d,e,f)==)num1=a+1.0*(d-a)*c/(c+f),num2=b+1.0*(e-b)*c/(c+f);
                else {
                    if(c>f){
                        num1=a+1.0*(d-a)*c/(c-f),num2=b+1.0*(e-b)*c/(c-f);
                    }
                    else {
                        num1=d+1.0*(a-d)*f/(f-c),num2=e+1.0*(b-e)*f/(f-c);
                    }
                }
                if(ct(g,h,i,a,b,c)==)num3=a+1.0*(g-a)*c/(c+i),num4=b+1.0*(h-b)*c/(c+i);
                else {
                    if(c>i){
                        num3=a+1.0*(g-a)*c/(c-i),num4=b+1.0*(h-b)*c/(c-i);
                    }
                    else {
                        num3=d+1.0*(a-g)*i/(i-c),num4=e+1.0*(b-h)*i/(i-c);
                    }
                }
                if(fabs(num3-num1)>eps||fabs(num4-num2)>eps)ret++;
            }
        }
        cout<<ret<<endl;
    }
    return ;
}

为什么老是说我颓废呢，，，，，我不颓废啊。

感觉，带修改莫队真是简单。

codeforces round#466

因为F一直不会，当时想到莫队，怎奈不会修改。

其实很简单，中午用了3分钟就看明白待修改莫队了。

然后F题就变成了大水题。。。

这场比赛应该AK的，，，，而我却没把握住机会。

多少有点遗憾吧。

A

给一个大小为n的集合，和一个常数d，问最少删除多少个数才能使得集合中，最大值与最小值相差小于k。

(不懂Doggu辣么强的选手为什么没有秒切并1A)

cf的div2T1从来不用什么算法。。。

sort之后枚举最大最小值即可。

#include<bits/stdc++.h>
using namespace std;
int a[];
int n,d;
int ans=;
int main(){
    cin>>n>>d;
    for(int i=;i<=n;i++){
        cin>>a[i];
    }
    sort(a+,a+n+);
    for(int i=;i<=n;i++){
        int ret=i-;
        for(int j=n;j>i;j--){
            if(a[j]-a[i]<=d)break;
            ret++;
        }
        ans=min(ans,ret);
    }
    cout<<ans;
    return ;
} 

B

给4个整数，n,k,A,B。

n每次可以-1或/k，代价分别是A,B问用最小代价使n变成1

不说了，直接上代码。都能看懂。

#include<bits/stdc++.h>
using namespace std;

#define ll long long
ll n,k,a,b;
ll ans=;
int main(){
    cin>>n>>k>>a>>b;
    if(k==){
        ans=(n-)*a;
        cout<<ans<<endl;
        return ;
    }
    while(n!=){
        if(n%k==){
            ll tt=(n-n/k)*a;
            ll t=b;
            ans+=min(t,tt);
            n=n/k;
        }
        else {
            if(n>k){
                ans+=(n%k)*a;
                n-=n%k;
            }
            else {
                ans+=(n-)*a;
                n=;
            }
        }
    }
    cout<<ans;
    return ;
} 

(Doggu这次没打好存粹是心态问题)

C

太水了，不说了，不说了。

前三题绝对是普及组难度的。

D

"We've tried solitary confinement, waterboarding and listening to Just In Beaver, to no avail. We need something extreme."

"Little Alena got an array as a birthday present..."

The array b of length n is obtained from the array a of length n and two integers l and r (l ≤ r) using the following procedure:

b1 = b2 = b3 = b4 = 0.

For all 5 ≤ i ≤ n:

• bi = 0 if ai, ai - 1, ai - 2, ai - 3, ai - 4 > r and bi - 1 = bi - 2 = bi - 3 = bi - 4 = 1
• bi = 1 if ai, ai - 1, ai - 2, ai - 3, ai - 4 < l and bi - 1 = bi - 2 = bi - 3 = bi - 4 = 0
• bi = bi - 1 otherwise

You are given arrays a and b' of the same length. Find two integers l and r (l ≤ r), such that applying the algorithm described above will yield an array b equal to b'.

It's guaranteed that the answer exists.

维护四个数，maxl,maxr,minl,minr。不断缩小范围即可。

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define inf 1000000000
int n;
int a[];
string b;
int maxl,maxr,minl,minr;
int main(){
    maxl=maxr=inf;
    minl=minr=-inf;
    cin>>n;
    for(int i=;i<n;i++)cin>>a[i];
    cin>>b;
    bool f1,f2;
    int L,R;
    for(int i=;i<n;i++){
        f1=f2=;
        if(b[i-]==''&&b[i-]==''&&b[i-]==''&&b[i-]=='')f1=;
        if(b[i-]==''&&b[i-]==''&&b[i-]==''&&b[i-]=='')f2=;
        L=min(min(a[i],min(a[i-],a[i-])),min(a[i-],a[i-])),R=max(max(a[i],max(a[i-],a[i-])),max(a[i-],a[i-]));
        int x=b[i]-'';
        int y=b[i-]-'';
        if(x==){
            if(y==){
                if(f2){
                    minr=max(L,minr);
                }
            }
            else {
                if(f1){
                    minl=max(R+,minl);
                }
            }
        }
        else {
            if(y==){
                if(f2){
                    maxr=min(maxr,L-);
                }
            }
            else {
                if(f1){
                    maxl=min(maxl,R);
                }
            }
        }
    }
    cout<<minl<<" "<<maxr<<endl;
    return ;
} 

E

Since you are the best Wraith King, Nizhniy Magazin «Mir» at the centre of Vinnytsia is offering you a discount.

You are given an array a of length n and an integer c.

The value of some array b of length k is the sum of its elements except for the 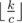 smallest. For example, the value of the array [3, 1, 6, 5, 2] with c = 2 is 3 + 6 + 5 = 14.

Among all possible partitions of a into contiguous subarrays output the smallest possible sum of the values of these subarrays.

Input

The first line contains integers n and c (1 ≤ n, c ≤ 100 000).

The second line contains n integers ai (1 ≤ ai ≤ 109) — elements of a.

Output

Output a single integer  — the smallest possible sum of values of these subarrays of some partition of a.

很容易得到一个小性质，选长度恰好为c的区间最优。

所以，st表求区间最小值。

dp[i]表示到i位置最大能刨去多大的数

dp[i]=max(dp[i-1],dp[i-10]+qmin(i-10+1,i))

ans=SUM-dp[n];

#include<bits/stdc++.h>
using namespace std;

#define ll long long
int rmq[][];
int lg[];
int n,c;
ll dp[];
ll sum;
int query(int l,int r){
    int k=lg[r-l+];
    return min(rmq[k][l],rmq[k][r-(<<k)+]);
}
int main(){
    cin>>n>>c;
    for(int i=;i<=n;i++)lg[i]=lg[i>>]+;
    for(int i=;i<=n;i++){
        cin>>rmq[][i];
        sum+=rmq[][i];
    }
    for(int i=;i<=;i++){
        for(int j=;j+(<<i)-<=n;j++){
            rmq[i][j]=min(rmq[i-][j],rmq[i-][j+(<<i-)]);
        }
    }
    for(int i=c;i<=n;i++){
        dp[i]=max(dp[i-],dp[i-c]+query(i-c+,i));
    }
    cout<<sum-dp[n];
    return ;
} 

F

带修改莫队裸题。

小结论，ans不超过2*sqrt(n)

#include<bits/stdc++.h>
using namespace std;
#define N 400010
map<int,int> ma;
inline int read(){
    int x=;char ch=getchar();
    while(ch<''||ch>'')ch=getchar();
    while(ch>=''&&ch<='')x=x*+ch-'',ch=getchar();
    return x;
}
int dd;
struct Q{
    int l,r,t,id;
}q[N];

struct C{
    int pos,x,o;
}c[N];

int block;
bool comp(Q u,Q v){
    return u.l/block<v.l/block || u.l/block==v.l/block && u.r/block<v.r/block || u.l/block==v.l/block && u.r/block==v.r/block && u.t<v.t;
}

int a[N];
int b[N];
int n,m;
int d[N];
int e[N];
void add(int x,int y){
    b[e[x]]--;
    e[x]+=y;
    b[e[x]]++;
}
int ans[N];
int main(){
    n=read(),m=read();
    for(int i=;i<=n;i++){
        a[i]=read();
        if(ma.count(a[i]))a[i]=ma[a[i]];
        else ma[a[i]]=++dd,a[i]=dd;
        d[i]=a[i];
    }
    block=ceil(pow(n,./));
    int cnt=;
    int cnt1=;
    int x,y,z;
    for(int i=;i<=m;i++){
        x=read(),y=read(),z=read();
        if(x==)q[++cnt].l=y,q[cnt].r=z,q[cnt].t=cnt1,q[cnt].id=cnt;
        else {
            if(ma.count(z))z=ma[z];
            else ma[z]=++dd,z=dd;
            c[++cnt1].pos=y,c[cnt1].x=z,c[cnt1].o=d[y];d[y]=z;
        }
    }
    int l,r,t;
    l=r=t=;
    sort(q+,q+cnt+,comp);
    for(int i=;i<=cnt;i++){
        while(r<q[i].r){
            r++;
            add(a[r],);
        }
        while(l>q[i].l){
            l--;
            add(a[l],);
        }
        while(r>q[i].r){
            if(r<=n)add(a[r],-);
            r--;
        }
        while(l<q[i].l){
            if(l)add(a[l],-);
            l++;
        }
        while(t<q[i].t){
            ++t;
            int pos=c[t].pos;
            a[pos]=c[t].x;
            if(pos>=l&&pos<=r)add(c[t].o,-),add(c[t].x,);
        }
        while(t>q[i].t){
            int pos=c[t].pos;
            a[pos]=c[t].o;
            if(pos>=l&&pos<=r)add(c[t].o,),add(c[t].x,-);
            t--;
        }
        for(int j=;j<=;j++){
            if(!b[j]){
                ans[q[i].id]=j;
                break;
            }
        }
    }
    for(int i=;i<=cnt;i++){
        printf("%d\n",ans[i]);
    }
    return ;
}