The Largest Clique UVA - 11324（ 强连通分量 + dp最长路）

这题  我刚开始想的是  缩点后  求出入度和出度为0 的点  然后统计个数  用总个数 减去

然而 这样是不可以的  画个图就明白了。。。

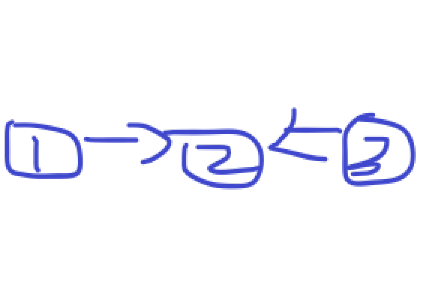
如果  减去度为0的点  那么最后如果出现这样的情况是不可以的

因为 1中的点  和  3 中的点不通。。

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define rap(a, n) for(int i=a; i<=n; i++)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
vector<int> G[];
int pre[maxn], low[maxn], sccno[maxn], dfs_clock, scc_cnt;
int w[maxn], line[maxn][maxn], d[maxn];
stack<int> s;
void dfs(int u)
{
    pre[u] = low[u] = ++dfs_clock;
    s.push(u);
    for(int i=; i<G[u].size(); i++)
    {
        int v = G[u][i];
        if(!pre[v])
        {
            dfs(v);
            low[u] = min(low[u], low[v]);
        }
        else if(!sccno[v])
            low[u] = min(low[u], pre[v]);
    }
    if(low[u] == pre[u])
    {
        scc_cnt++;
        for(;;)
        {
            int x = s.top(); s.pop();
            sccno[x] = scc_cnt;
            if(x == u) break;
        }
    }
}

void init()
{
    dfs_clock = scc_cnt = ;
    mem(sccno, );
    mem(pre, );
    mem(w, );
    mem(d, -);
    mem(line, );
    for(int i=; i<maxn; i++) G[i].clear();
}

int dp(int u)
{
    int& ans = d[u];
    if(ans >= ) return ans;
    ans = w[u];      //最后一个点后边就没有点了
    for(int i=; i<=scc_cnt; i++)
        if(u != i && line[u][i])
            ans = max(ans, dp(i) + w[u]);
    return ans;
}

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        init();
        int n, m;
        scanf("%d%d", &n, &m);
        for(int i=; i<=m; i++)
        {
            int u, v;
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
        }
        for(int i=; i<=n; i++)
            if(!pre[i])
                dfs(i);
        for(int i=; i<=n; i++)
        {
            w[sccno[i]]++;   //统计每个强连通分量里的点的个数
            for(int j=; j<G[i].size(); j++)
                line[sccno[i]][sccno[G[i][j]]] = ;
        }
        int res = ;
        for(int i=; i<=scc_cnt; i++)  // 以每一个点为起点 去找最长路
            res = max(res, dp(i));

        printf("%d\n", res);

    }

    return ;
}