[javaSE] 数据结构（AVL树基本概念）

AVL树是高度平衡的二叉树，任何节点的两个子树的高度差别<=1

实现AVL树

定义一个AVL树，AVLTree，定义AVLTree的节点内部类AVLNode，节点包含以下特性：

1.key——关键字，对AVL树的节点进行排序

2.left——左子树

3.right——右子树

4.height——高度

如果在AVL树插入节点后可能导致AVL树失去平衡，具体会有四种状态：

LL：左左，LeftLeft

LR：左右，LeftRight

RL：右左，RightLeft

RR：右右，RightRight

解决上面的情况

解决LL，需要左单旋转

解决RR，需要右单旋转

解决LR，需要先右单旋转，再左单旋转

解决RL，需要先左单旋转，再右单旋转

实现左单旋转

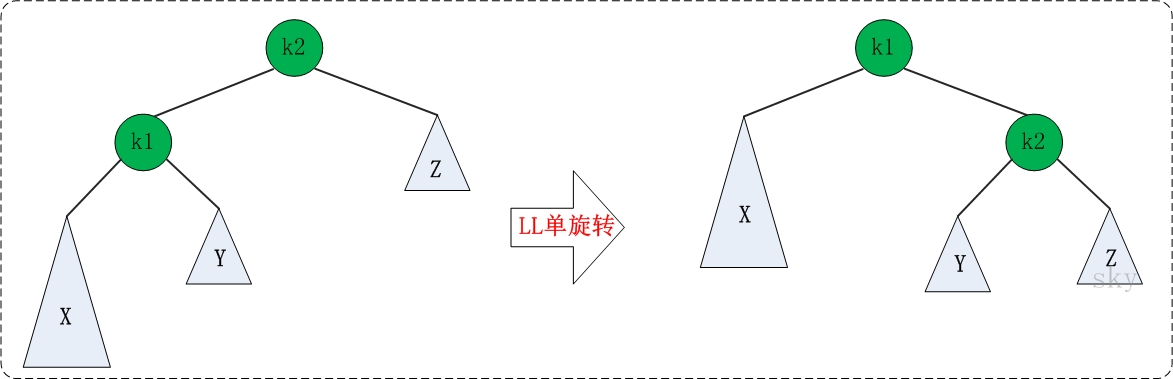
k1，k2

k2的left给k1

k1的right给k2的left

k2给k1的right

实现右单旋转

k1，k2

k1的right给k2

k2的left给k1的right

k1给k2的left

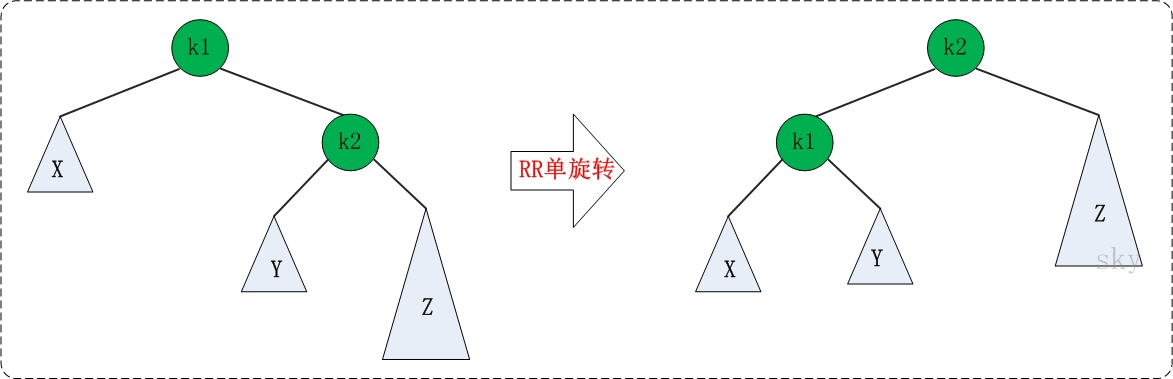
节点的高度，是它左子树或者右子树中，高度大的那个 再加1

/**
 * AVL树测试
 * @author taoshihan
 * @param <T>
 *
 */
public class AVLTree<T extends Comparable<T>> {
    private AVLNode mRoot;//根节点
    class AVLNode<T extends Comparable<T>>{
        private T key;//键值
        private int height;//高度
        private AVLNode left;//左子树
        private AVLNode right;//右子树
        public AVLNode(T key,AVLNode left,AVLNode right) {
            this.key=key;
            this.left=left;
            this.right=right;
            this.height=0;
        }
    }
    /**
     * 获取节点高度
     * @param tree
     * @return
     */
    public int height(AVLNode<T> tree){
        if(tree!=null){
            return tree.height;
        }
        return 0;
    }
    /**
     * 取出左右子树中高的那个
     * @param a
     * @param b
     * @return
     */
    public int maxHeight(int a,int b){
        return a>b ? a : b;
    }
    /**
     * 左单旋转
     * @param k2
     * @return
     */
    public AVLNode<T> leftLeftRotation(AVLNode<T> k2){
        AVLNode k1;
        k1 = k2.left;
        k2.left=k1.right;
        k1.right=k2;
        k2.height=maxHeight(height(k2.left), height(k2.right));
        k1.height=maxHeight(height(k1.left), height(k1.right));
        return k1;
    }
    /**
     * 右单旋转
     * @param k2
     * @return
     */
    public AVLNode<T> rightRightRotation(AVLNode<T> k1){
        AVLNode k2;
        k2=k1.right;
        k1.right=k2.left;
        k2.left=k1;

        k2.height=maxHeight(height(k2.left), height(k2.right));
        k1.height=maxHeight(height(k1.left), height(k1.right));
        return k2;
    }