如何用Python实现常见机器学习算法-3
三、BP神经网络
1、神经网络模型
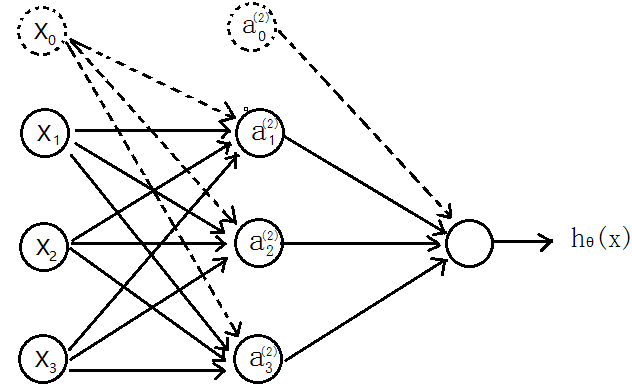
首先介绍三层神经网络,如下图
输入层(input layer)有三个units( 为补上的bias,通常设为1)
为补上的bias,通常设为1)
 表示第j层的第i个激励,也称为单元unit
表示第j层的第i个激励,也称为单元unit
 为第j层到第j+1层映射的权重矩阵,就是每条边的权重
为第j层到第j+1层映射的权重矩阵,就是每条边的权重
所以可以得到:
隐含层:
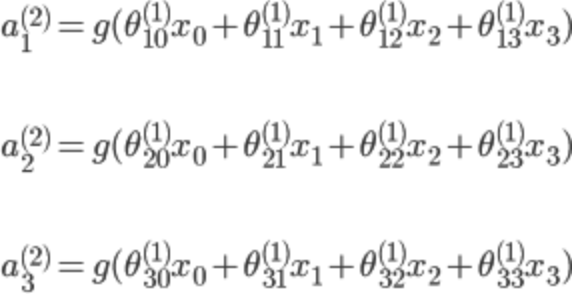
输出层:

其中,S型函数 ,也成为激励函数
,也成为激励函数
可以看出 为3✖️4的矩阵,
为3✖️4的矩阵, 为1✖️4的矩阵
为1✖️4的矩阵
 ==》j+1的单元数x(j层的单元数+1)
==》j+1的单元数x(j层的单元数+1)
2、代价函数
假设最后输出的 ,即代表输出层有K个单元
,即代表输出层有K个单元
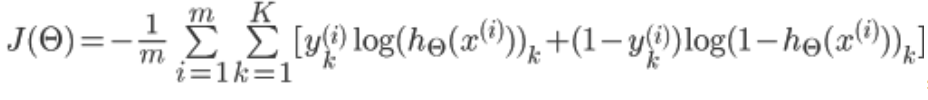
其中, 代表第i个单元输出与逻辑回归的代价函数
代表第i个单元输出与逻辑回归的代价函数
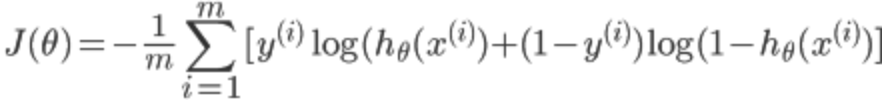
差不多,就是累加上每个输出(共有K个输出)
3、正则化
L-->所有层的个数
 -->第l层unit的个数
-->第l层unit的个数
正则化后的代价函数为

 共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
正则化后的代价函数实现代码:
- # 代价函数
- def nnCostFunction(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda):
- length = nn_params.shape[0] # theta的中长度
- # 还原theta1和theta2
- Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1)
- Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1)
- # np.savetxt("Theta1.csv",Theta1,delimiter=',')
- m = X.shape[0]
- class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系
- # 映射y
- for i in range(num_labels):
- class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
- '''去掉theta1和theta2的第一列,因为正则化时从1开始'''
- Theta1_colCount = Theta1.shape[1]
- Theta1_x = Theta1[:,1:Theta1_colCount]
- Theta2_colCount = Theta2.shape[1]
- Theta2_x = Theta2[:,1:Theta2_colCount]
- # 正则化向theta^2
- term = np.dot(np.transpose(np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))),np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1))))
- '''正向传播,每次需要补上一列1的偏置bias'''
- a1 = np.hstack((np.ones((m,1)),X))
- z2 = np.dot(a1,np.transpose(Theta1))
- a2 = sigmoid(z2)
- a2 = np.hstack((np.ones((m,1)),a2))
- z3 = np.dot(a2,np.transpose(Theta2))
- h = sigmoid(z3)
- '''代价'''
- J = -(np.dot(np.transpose(class_y.reshape(-1,1)),np.log(h.reshape(-1,1)))+np.dot(np.transpose(1-class_y.reshape(-1,1)),np.log(1-h.reshape(-1,1)))-Lambda*term/2)/m
- return np.ravel(J)
4、反向传播BP
上面正向传播可以计算得到J(θ),使用梯度下降算法还需要求它的梯度
BP反向传播的目的就是求代价函数的梯度
假设4层的神经网络, 记为-->l层第j个单元的误差
记为-->l层第j个单元的误差
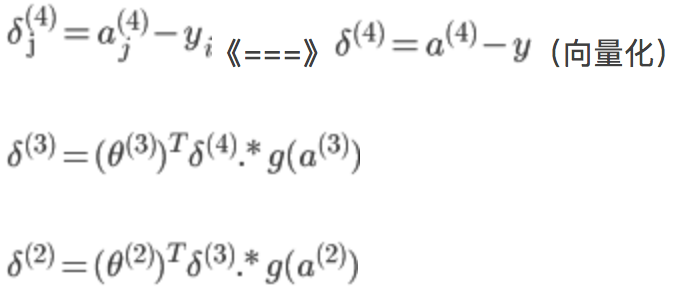
没有 ,因为对于输入没有误差,因为S型函数
,因为对于输入没有误差,因为S型函数 的倒数为:
的倒数为:

所以上面的 和
和 可以在前向传播中计算出来
可以在前向传播中计算出来
反向传播计算梯度的过程为:

for i=1-m:

正向传播计算 (l=2,3,4...L)
(l=2,3,4...L)
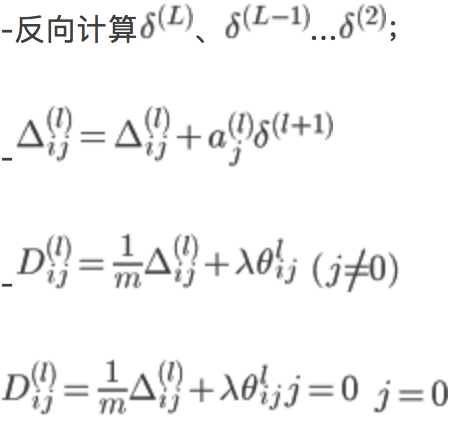
最后 ,即得到代价函数的梯度
,即得到代价函数的梯度
代码实现:
- # 梯度
- def nnGradient(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda):
- length = nn_params.shape[0]
- Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1)
- Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1)
- m = X.shape[0]
- class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系
- # 映射y
- for i in range(num_labels):
- class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
- '''去掉theta1和theta2的第一列,因为正则化时从1开始'''
- Theta1_colCount = Theta1.shape[1]
- Theta1_x = Theta1[:,1:Theta1_colCount]
- Theta2_colCount = Theta2.shape[1]
- Theta2_x = Theta2[:,1:Theta2_colCount]
- Theta1_grad = np.zeros((Theta1.shape)) #第一层到第二层的权重
- Theta2_grad = np.zeros((Theta2.shape)) #第二层到第三层的权重
- Theta1[:,0] = 0;
- Theta2[:,0] = 0;
- '''正向传播,每次需要补上一列1的偏置bias'''
- a1 = np.hstack((np.ones((m,1)),X))
- z2 = np.dot(a1,np.transpose(Theta1))
- a2 = sigmoid(z2)
- a2 = np.hstack((np.ones((m,1)),a2))
- z3 = np.dot(a2,np.transpose(Theta2))
- h = sigmoid(z3)
- '''反向传播,delta为误差,'''
- delta3 = np.zeros((m,num_labels))
- delta2 = np.zeros((m,hidden_layer_size))
- for i in range(m):
- delta3[i,:] = h[i,:]-class_y[i,:]
- Theta2_grad = Theta2_grad+np.dot(np.transpose(delta3[i,:].reshape(1,-1)),a2[i,:].reshape(1,-1))
- delta2[i,:] = np.dot(delta3[i,:].reshape(1,-1),Theta2_x)*sigmoidGradient(z2[i,:])
- Theta1_grad = Theta1_grad+np.dot(np.transpose(delta2[i,:].reshape(1,-1)),a1[i,:].reshape(1,-1))
- '''梯度'''
- grad = (np.vstack((Theta1_grad.reshape(-1,1),Theta2_grad.reshape(-1,1)))+Lambda*np.vstack((Theta1.reshape(-1,1),Theta2.reshape(-1,1))))/m
- return np.ravel(grad)
5、BP可以求梯度的原因
实际是利用了链式求导法则
因为下一层的单元利用上一层的单元作为输入进行计算
大体的推导过程如下,最终我们是想预测函数与已知的y非常接近,求均方差的梯度沿着此梯度方向可使代价函数最小化。可对照上面求梯度的过程。
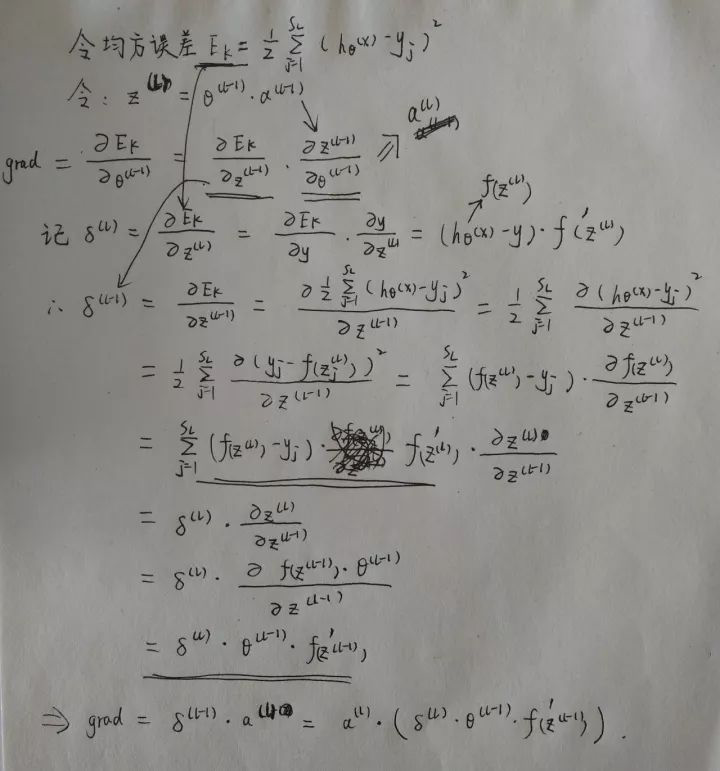
求误差更详细的推导过程:
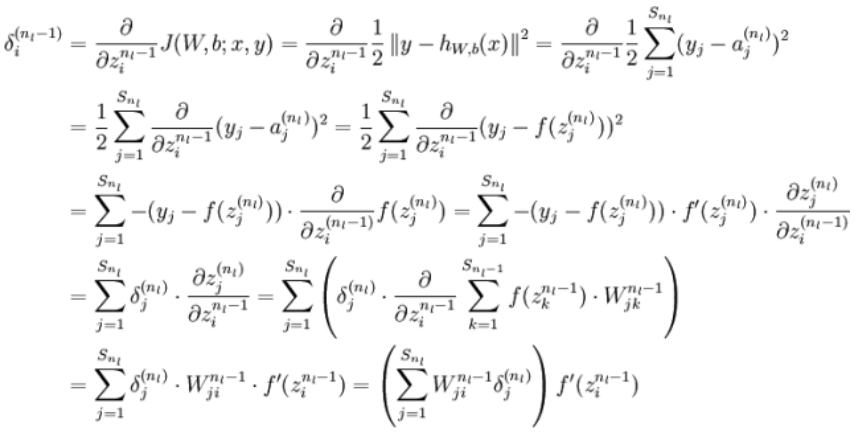
6、梯度检查
检查利用BP求的梯度是否正确
利用导数的定义验证:
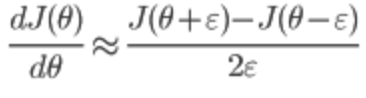
求出来的数值梯度应该与BP求出的梯度非常接近
验证BP正确后就不需要再执行验证梯度的算法了
代码实现
- # 检验梯度是否计算正确
- # 检验梯度是否计算正确
- def checkGradient(Lambda = 0):
- '''构造一个小型的神经网络验证,因为数值法计算梯度很浪费时间,而且验证正确后之后就不再需要验证了'''
- input_layer_size = 3
- hidden_layer_size = 5
- num_labels = 3
- m = 5
- initial_Theta1 = debugInitializeWeights(input_layer_size,hidden_layer_size);
- initial_Theta2 = debugInitializeWeights(hidden_layer_size,num_labels)
- X = debugInitializeWeights(input_layer_size-1,m)
- y = 1+np.transpose(np.mod(np.arange(1,m+1), num_labels))# 初始化y
- y = y.reshape(-1,1)
- nn_params = np.vstack((initial_Theta1.reshape(-1,1),initial_Theta2.reshape(-1,1))) #展开theta
- '''BP求出梯度'''
- grad = nnGradient(nn_params, input_layer_size, hidden_layer_size,
- num_labels, X, y, Lambda)
- '''使用数值法计算梯度'''
- num_grad = np.zeros((nn_params.shape[0]))
- step = np.zeros((nn_params.shape[0]))
- e = 1e-4
- for i in range(nn_params.shape[0]):
- step[i] = e
- loss1 = nnCostFunction(nn_params-step.reshape(-1,1), input_layer_size, hidden_layer_size,
- num_labels, X, y,
- Lambda)
- loss2 = nnCostFunction(nn_params+step.reshape(-1,1), input_layer_size, hidden_layer_size,
- num_labels, X, y,
- Lambda)
- num_grad[i] = (loss2-loss1)/(2*e)
- step[i]=0
- # 显示两列比较
- res = np.hstack((num_grad.reshape(-1,1),grad.reshape(-1,1)))
- print res
7、权重的随机初始化
神经网络不能像逻辑回归那样初始化theta为0,因为若是每条边的权重都为0,每个神经元都是相同的输出,在反向传播中也会得到同样的梯度,最终只会预测一种结果。
所以应该初始化为接近0的数
代码实现
- # 随机初始化权重theta
- def randInitializeWeights(L_in,L_out):
- W = np.zeros((L_out,1+L_in)) # 对应theta的权重
- epsilon_init = (6.0/(L_out+L_in))**0.5
- W = np.random.rand(L_out,1+L_in)*2*epsilon_init-epsilon_init # np.random.rand(L_out,1+L_in)产生L_out*(1+L_in)大小的随机矩阵
- return W
8、预测
正向传播预测结果
代码实现
- # 预测
- def predict(Theta1,Theta2,X):
- m = X.shape[0]
- num_labels = Theta2.shape[0]
- #p = np.zeros((m,1))
- '''正向传播,预测结果'''
- X = np.hstack((np.ones((m,1)),X))
- h1 = sigmoid(np.dot(X,np.transpose(Theta1)))
- h1 = np.hstack((np.ones((m,1)),h1))
- h2 = sigmoid(np.dot(h1,np.transpose(Theta2)))
- '''
- 返回h中每一行最大值所在的列号
- - np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率)
- - 最后where找到的最大概率所在的列号(列号即是对应的数字)
- '''
- #np.savetxt("h2.csv",h2,delimiter=',')
- p = np.array(np.where(h2[0,:] == np.max(h2, axis=1)[0]))
- for i in np.arange(1, m):
- t = np.array(np.where(h2[i,:] == np.max(h2, axis=1)[i]))
- p = np.vstack((p,t))
- return p
9、输出结果
梯度检查

随机显示100个手写数字

显示theta1权重
训练集预测准确度
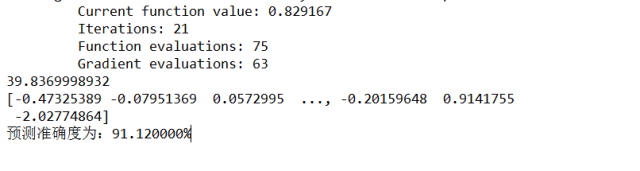
归一化后训练集预测准确度

如何用Python实现常见机器学习算法-3的更多相关文章
- 如何用Python实现常见机器学习算法-1
最近在GitHub上学习了有关python实现常见机器学习算法 目录 一.线性回归 1.代价函数 2.梯度下降算法 3.均值归一化 4.最终运行结果 5.使用scikit-learn库中的线性模型实现 ...
- 如何用Python实现常见机器学习算法-2
二.逻辑回归 1.代价函数 可以将上式综合起来为: 其中: 为什么不用线性回归的代价函数表示呢?因为线性回归的代价函数可能是非凸的,对于分类问题,使用梯度下降很难得到最小值,上面的代价函数是凸函数的图 ...
- 如何用Python实现常见机器学习算法-4
四.SVM支持向量机 1.代价函数 在逻辑回归中,我们的代价为: 其中: 如图所示,如果y=1,cost代价函数如图所示 我们想让,即z>>0,这样的话cost代价函数才会趋于最小(这正是 ...
- python 的常见排序算法实现
python 的常见排序算法实现 参考以下链接:https://www.cnblogs.com/shiluoliming/p/6740585.html 算法(Algorithm)是指解题方案的准确而完 ...
- 用Python实现常见排序算法
最简单的排序有三种:插入排序,选择排序和冒泡排序.这三种排序比较简单,它们的平均时间复杂度均为O(n^2),在这里对原理就不加赘述了.贴出来源代码. 插入排序: def insertion_sort( ...
- python实现常见排序算法
#coding=utf-8from collections import deque #冒泡排序def bubblesort(l):#复杂度平均O(n*2) 最优O(n) 最坏O(n*2) for i ...
- 建模分析之机器学习算法(附python&R代码)
0序 随着移动互联和大数据的拓展越发觉得算法以及模型在设计和开发中的重要性.不管是现在接触比较多的安全产品还是大互联网公司经常提到的人工智能产品(甚至人类2045的的智能拐点时代).都基于算法及建模来 ...
- 10 种机器学习算法的要点(附 Python 和 R 代码)
本文由 伯乐在线 - Agatha 翻译,唐尤华 校稿.未经许可,禁止转载!英文出处:SUNIL RAY.欢迎加入翻译组. 前言 谷歌董事长施密特曾说过:虽然谷歌的无人驾驶汽车和机器人受到了许多媒体关 ...
- 10 种机器学习算法的要点(附 Python)(转载)
一.前言 谷歌董事长施密特曾说过:虽然谷歌的无人驾驶汽车和机器人受到了许多媒体关注,但是这家公司真正的未来在于机器学习,一种让计算机更聪明.更个性化的技术 也许我们生活在人类历史上最关键的时期:从使用 ...
随机推荐
- flow flow-typed 定义简单demo
flow-typed 安装 全局 npm install -g flow-typed 测试代码 一个简单全局函数 目录根目录 flow-typed userLibDef.js declare func ...
- list_for_each与list_for_each_entry具体解释
一.list_for_each 1.list_for_each原型#define list_for_each(pos, head) \ for (pos = (head)->next, ...
- macOS -- Mac系统如何通过终端使用mysql
打开终端,输入下面的命令 mysql -u root -p 如果提示输入密码,并且能直接进入,那就太棒了,下面的就不用看了,直接使用就好了 如果没有这么幸运,提示 command not found ...
- 转HTTP协议 --- Cookie
转自:http://www.cnblogs.com/TankXiao/archive/2013/04/15/2848906.html Cookie是HTTP协议中非常重要的东西, 之前拜读了Fish ...
- Web验证方式(2)--Form Authentication
Form验证方式并不是HTTP标准,而是在微软ASP.NET Web框架下提供的一种验证方式.其大致流程如下: 在上图的流程中,ASP.NET框架提供了如下支持类:( FormsAuthenticat ...
- JAVA通过JDBC连接Oracle数据库详解【转载】
JAVA通过JDBC连接Oracle数据库详解 (2011-03-15 00:10:03) 转载▼http://blog.sina.com.cn/s/blog_61da86dd0100q27w.htm ...
- Android 查看Android版本的方法
1.通过源码查看 Android 版本 路径:build/core/version_defaults.mk PLATFORM_VERSION := 2.通过编译时终端输出查看 ============ ...
- erlang和ruby互相调用
erlang调用ruby https://github.com/mojombo/erlectricity ruby调用erlang https://github.com/davebryson/rint ...
- Bootstrap-CL:徽章
ylbtech-Bootstrap-CL:徽章 1.返回顶部 1. Bootstrap 徽章(Badges) 本章将讲解 Bootstrap 徽章(Badges).徽章与标签相似,主要的区别在于徽章的 ...
- maven install 跳过测试
mvn命令跳过测试:mvn install -Dmaven.test.skip=true 测试类不会生成.class 文件mvn install -DskipTests 测试类会生成.class文件 ...
