为什么样本方差除以（n-1）而不是n ?（自由度）

　　不记得第几次看见样本方差的公式，突然好奇为什么要除以（n-1）而不是n呢？看见一篇文章从定义上和无偏估计推导上讲的很清楚https://blog.csdn.net/fuming2021118535/article/details/51290320，书上看见从自由度上作的解释，在此记录一下。

　　自由度

　　自由度是统计学中一个经常见到的重要概念。指计算某一统计量时，取值不受限制的变量个数。

　　对于样本方差来说，自由度为n-1。S²的表达式中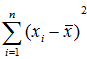为n个量的平方和，为何自由度只有n-1?因为x₁-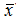, ... , x₂-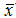这n个量并不能自由变化，而是受到一个约束，即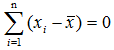，这使它的自由度少了一个，在样本方差S²的公式中分母上是n-1，就是因为当给定均值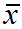时，x₁, x₂, ..., x_n这n个数据中，前n-1个数据都可以自由取值，而第n个数据受到全部数据的平均值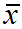的约束，不能自由取值。第n个数据可由公式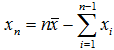求得，因此，S²的自由度是n-1。所以，所谓“自由度”就是指可以自由取值的数据的个数，或者指不受任何约束，可以自由变动的变量的个数。

　　还可以对自由度这个概念赋予另一种解释，即一共有n个数据，有n个自由度，用S²估计总体方差σ²，自由度本应为n，但总体均值μ也未知，用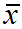去估计，用掉了一个自由度，故只剩n-1个自由度。

　　用矩阵秩的概念也可以解释自由度。自由度是对随机变量的二次型（可称为二次统计量）而言的，自由度就是二次型矩阵的秩。但用矩阵的秩来判断统计量的自由度比较困难，一般采用直观方法来做判断，即由线性代数知识可知，一个二次型的秩为它所含变量个数减去变量间独立线性约束条件的个数，从而便可得到统计量的自由度。关于样本方差S²的自由度，就是因为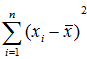含有n个变量，但n个变量有一个线性约束条件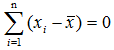，故S²的自由度为n-1。

　　回归分析中，回归方程的显著性检验用到残差平方和。确定残差平方和的自由度的一般方法是：观测值的个数n减去必须估计出的参数的个数就是自由度。例如p元线性回归方程的残差平方和的自由度就是n-p-1，因为回归方程中有p+1个待估参数。