Leetcode 1008. 先序遍历构造二叉树

1008. 先序遍历构造二叉树

 显示英文描述

我的提交返回竞赛

 

• 用户通过次数169
• 用户尝试次数183
• 通过次数171
• 提交次数247
• 题目难度Medium

返回与给定先序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。

(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，先序遍历首先显示节点的值，然后遍历 node.left，接着遍历 node.right。）

示例：

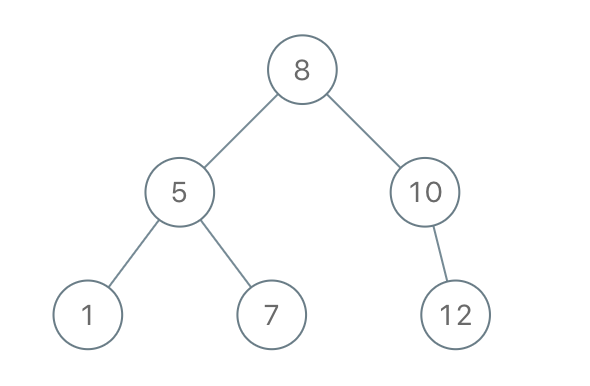
输入：[8,5,1,7,10,12]
输出：[8,5,10,1,7,null,12]

提示：

1. 1 <= preorder.length <= 100
2. 先序 preorder 中的值是不同的。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    TreeNode* dfs(vector<int> v,int start,int end){
        if(start > end) return NULL;
        TreeNode* p = new TreeNode(v[start]);
        if(start == end) return p;
        int cnt=start;
        for(int i=start+;i <= end;i++){
            if(v[i]<v[start])cnt = i;
            else break;
        }
        p->left = dfs(v,start+,cnt);
        p->right = dfs(v,cnt+,end);
        return p;
    }

    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return dfs(preorder,,preorder.size()-);
    }
};

_我写的和大佬写的

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* bstFromPreorder(vector<int>& a) {
        int n = a.size();
        if (n == ) return NULL;
        TreeNode *it = new TreeNode(a[]);
        vector<int> L, R;
        for (auto x : a)
        {
            if (x < a[]) L.push_back(x);
            if (x > a[]) R.push_back(x);
        }
        it->left = bstFromPreorder(L);
        it->right = bstFromPreorder(R);
        return it;
    }
};

——这写法也太吊了吧，太美了！