【CART与GBDT】

一、CART（分类回归树）

   1.思想：

    一种采用基尼信息增益作为划分属性的二叉决策树。基尼指数越小，表示纯度越高。

 2.回归：

每个节点都有一个预测值，预测值等于属于该节点的所有样例的平均值，分支时，选择每个属性的每个阈值的最好分割点，衡量的标准是最小化均方差。

训练：对训练样本的第i（1<=i<=n）个属性,穷举每个分割点，找到均方差最小的分割点进行分割，该节点的值设为落到该节点的训练样本的平均值，直到不可分或者到一定高度或者属性使用完或者均方差不下降。

测试：对测试样本按照训练时的分割点进行下落，落到叶节点，叶节点的平均值即为预测值。

二、GBDT（梯度提升决策树）

   1.原理：

     用多棵回归树（或多个弱分类器）进行集成，其中的多棵树不是独立的，而是后面的树在前者的基础上学习误差，所有树的结果加起来是预测得到的结果。弱分类器一般采用CART。

     2.过程：

     原始回归树：

    

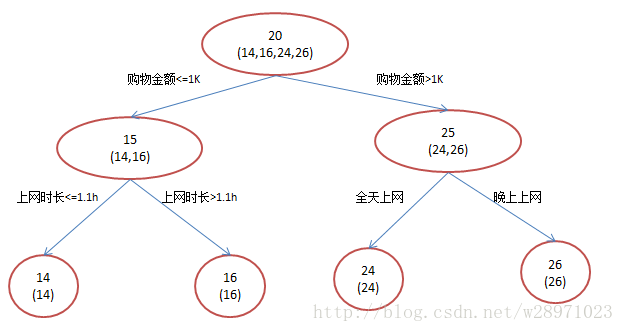
GBDT：

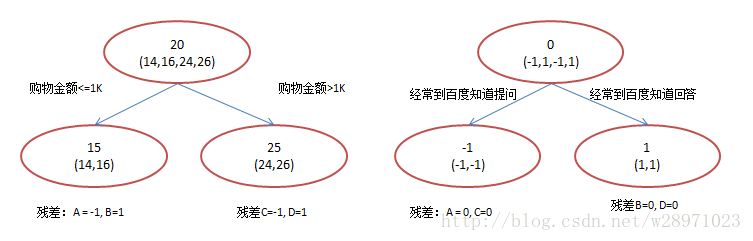
     3.依据：

     防止过拟合；

残差计算变相增大了分错样本的权重，分对的趋于0，这样后续的树就能专注于学习分错的样本；

每一步都用残差作为全局最优的梯度方向，并没有真实计算梯度；

每一次都走一小步，逐渐逼近目标，比每次都走一大步逼近目标更能防止过拟合。

4.优缺点：

优点：鲁棒性比较好，准确率比较高。

缺点：弱分类器间存在依赖关系，无法并行训练。

5.问题：

（1）训练过程：

gbdt通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练，通过降低偏差来不断提高最终分类器的精度。

（2）如何选择特征：

如CART，对每个节点的每个切分点进行遍历，选择基尼指数最小的。

（3）如何构建特征：

利用gbdt去产生特征的组合，以叶子结点为基，在基下的表示即为特征。

（4）如何用于分类：

针对样本 X 每个可能的类都训练一个分类回归树。

     6.参考：

      https://www.cnblogs.com/peizhe123/p/6105696.html

https://www.cnblogs.com/pinard/p/6140514.html

https://www.cnblogs.com/ModifyRong/p/7744987.html

三、Xgboost

   1.思想：

   Xgboost是GB算法的高效实现，xgboost中的基学习器除了可以是CART（gbtree）也可以是线性分类器（gblinear）

   2.区别：

   （1）xgboost在目标函数中显示的加上了正则化项，基学习为CART时，正则化项与树的叶子节点的数量T和叶子节点的值有关。

（2）GB中使用Loss Function对f(x)的一阶导数计算出伪残差用于学习生成fm(x)，xgboost不仅使用到了一阶导数，还使用二阶导数。

（3）CART回归树中寻找最佳分割点的衡量标准是最小化均方差，xgboost寻找分割点的标准是最大化一个函数。

3.参考：

https://www.cnblogs.com/wxquare/p/5541414.html