Codeforces 817C Really Big Numbers - 二分法 - 数论
Ivan likes to learn different things about numbers, but he is especially interested in really big numbers. Ivan thinks that a positive integer number x is really big if the difference between x and the sum of its digits (in decimal representation) is not less than s. To prove that these numbers may have different special properties, he wants to know how rare (or not rare) they are — in fact, he needs to calculate the quantity of really big numbers that are not greater than n.
Ivan tried to do the calculations himself, but soon realized that it's too difficult for him. So he asked you to help him in calculations.
The first (and the only) line contains two integers n and s (1 ≤ n, s ≤ 1018).
Print one integer — the quantity of really big numbers that are not greater than n.
12 1
3
25 20
0
10 9
1
In the first example numbers 10, 11 and 12 are really big.
In the second example there are no really big numbers that are not greater than 25 (in fact, the first really big number is 30: 30 - 3 ≥ 20).
In the third example 10 is the only really big number (10 - 1 ≥ 9).
题目大意 设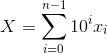 ,
, 定义
定义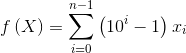 ,求满足
,求满足 的X有 多少个。
的X有 多少个。
随便举几个数10, 20, 30, 100,然后发现对应的函数值的分别为9, 18, 27和99猜测它满足"单调性"。
现在来证明一下,当A > B时,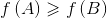 。
。
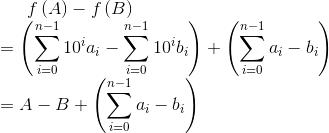
当最高的不相同的位数为k,则A - B的最小值为$10^{k - 1}$,后面的各位数字之差最小为 -9(k - 1)(个位为第1位),显然这两个数的和大于等于0。
所以就可以二分出第一个满足要求的数,然后算一算就好了。
Code
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cmath>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <sstream>
#include <algorithm>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <vector>
#include <stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << ) - );
const signed long long llf = (signed long long)((1ull << ) - );
const double eps = 1e-;
const int binary_limit = ;
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
char x;
int aFlag = ;
while(!isdigit((x = getchar())) && x != '-' && x != -);
if(x == -) {
ungetc(x, stdin);
return false;
}
if(x == '-'){
x = getchar();
aFlag = -;
}
for(u = x - ''; isdigit((x = getchar())); u = (u * ) + x - '');
ungetc(x, stdin);
u *= aFlag;
return true;
} #define LL long long LL n, s; inline void init() {
readInteger(n);
readInteger(s);
} boolean check(LL x) {
LL y = x, bitsum = ;
while(y) bitsum += y % , y /= ;
return x - bitsum >= s;
} inline void solve() {
LL l = , r = n;
while(l <= r) {
LL mid = (l + r) >> ;
if(check(mid)) r = mid - ;
else l = mid + ;
}
printf(Auto"\n", n - r);
} int main() {
init();
solve();
return ;
}
Codeforces 817C Really Big Numbers - 二分法 - 数论的更多相关文章
- [codeforces 55]D. Beautiful numbers
[codeforces 55]D. Beautiful numbers 试题描述 Volodya is an odd boy and his taste is strange as well. It ...
- Really Big Numbers CodeForces - 817C (数学规律+二分)
C. Really Big Numbers time limit per test 1 second memory limit per test 256 megabytes input standar ...
- Codeforces Round #382 Div. 2【数论】
C. Tennis Championship(递推,斐波那契) 题意:n个人比赛,淘汰制,要求进行比赛双方的胜场数之差小于等于1.问冠军最多能打多少场比赛.题解:因为n太大,感觉是个构造.写写小数据, ...
- Codeforces Beta Round #17 D. Notepad (数论 + 广义欧拉定理降幂)
Codeforces Beta Round #17 题目链接:点击我打开题目链接 大概题意: 给你 \(b\),\(n\),\(c\). 让你求:\((b)^{n-1}*(b-1)\%c\). \(2 ...
- CodeForces - 1245A Good ol' Numbers Coloring (思维)
Codeforces Round #597 (Div. 2 Consider the set of all nonnegative integers: 0,1,2,-. Given two integ ...
- CodeForces 682A Alyona and Numbers (水题)
Alyona and Numbers 题目链接: http://acm.hust.edu.cn/vjudge/contest/121333#problem/A Description After fi ...
- Codeforces 449D Jzzhu and Numbers
http://codeforces.com/problemset/problem/449/D 题意:给n个数,求and起来最后为0的集合方案数有多少 思路:考虑容斥,ans=(-1)^k*num(k) ...
- HDU1058 Humble Numbers 【数论】
Humble Numbers Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) T ...
- Codeforces 396B On Sum of Fractions 数论
题目链接:Codeforces 396B On Sum of Fractions 题解来自:http://blog.csdn.net/keshuai19940722/article/details/2 ...
随机推荐
- .net core 路由处理请求流程图
- java生成随机六位数的验证码&随机生成十位数ValidCode码,用于邮件的验证&检查是不是符合为合法的中国的手机号码
package com.demo.test1; import java.security.NoSuchAlgorithmException; import java.security.SecureRa ...
- install scala & spark env
安装Scala 1,到http://www.scala-lang.org/download/ 下载与Spark版本对应的Scala.Spark1.2对应于Scala2.10的版本.这里下载scala- ...
- PHP语句函数
运算符 +.-.*./.++.--.+=.-=.% 字符串拼接用. js里面用+拼接 逻辑运算符 and && . or || . ! 错误运算符 @(可以抑制错误) ...
- [3]传奇3服务器源码分析一 DBServer
留存 服务端下载地址: 点击这里
- html5-相对定位
*{ margin: 0px; padding: 0px;}div{ width: 300px; height: 300px;}#div1{ background: rg ...
- 使用Groovy+Spock构建可配置的订单搜索接口测试用例集
概述 测试是软件成功上线的安全网.基本的测试包含单元测试.接口测试.在 "使用Groovy+Spock轻松写出更简洁的单测" 一文中已经讨论了使用GroovySpock编写简洁的单 ...
- flask 单个页面多个表单(单视图处理、多视图处理)
单个页面多个表单 除了在单个表单上实现多个提交按钮,有时还需要在单个页面上创建多个表单.比如,在程序的主页上同时添加登录和注册表单.当在同一个页面上添加多个表单时,我们需要解决的问题是在视图函数中判断 ...
- Mysql相关技术细节整理
一.错误日志相关 1.mysql错误日志所在位置 windows下,错误日志文件一般在安装目录下的data目录下.扩展名是.err的文件,也可以打开安装目录下的my.ini文件检查一下linux下,错 ...
- 项目方说性能达到百万TPS,如何测试它的可信度?
项目方说性能达到百万TPS,如何测试它的可信度? 应用系统性能提升的关键在于运维端的接入管理模型(AAA,认证 Authentication.授权 Authorization.计费 Accountin ...
