HDU 4557 Tree（可持久化字典树 + LCA）

http://acm.hdu.edu.cn/showproblem.php?pid=4757

题意：

给出一棵树，每个结点有一个权值，现在有多个询问，每次询问包含x，y，z三个数，求出在x到y的路径上与z最大的异或值。

思路：

看着别人的代码做完这道题目之后觉得这题和主席树求第k小是异曲同工的，主席树求第k小是对每个数建立一棵线段树，也就是说第i棵线段树记录的是区间[1,i]之间的数，这样的话[l,r]这个区间内的数就在第l棵线段树和第r棵线段树之间。

回到这题上来，这题也是要在一个范围之内寻找一个值，但是它不是数组，而是树结构，所以类似的也可以对每个结点建立字典树，记录根结点到该结点的所有权值。图解如下：

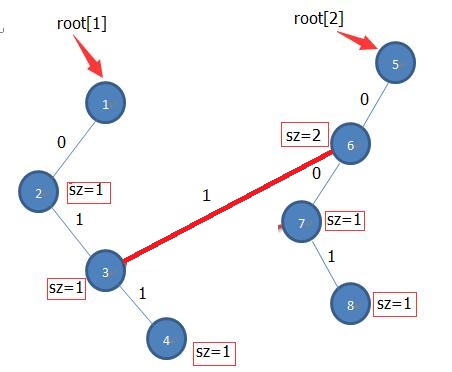
假设现在只有两个结点1和2,1是2的父亲结点，1的权值为3,2的权值为1。对1建立字典树如图左所示，对2建立字典树时如图右所示，5->6->7->8就是结点2的字典树，5->6->3->4就是结点1的字典树。所以我们对某个结点建立字典树时，就包含了根结点到该结点路径上所有点权值的情况。图中的sz表示的就是前缀出现的数量，为什么root[2]的前缀0的sz是2呢，因为一个来自1结点的，另一个是自己的，所有在计算sz值的时候，先继承父亲结点的sz，然后再加上自身的。

有了这个sz值之后，我们就可以进行查询操作了，先计算出x和y的最近公共祖先z，那么如果判断前缀是否存在就是t[t[x].son[!c]].sz+t[t[y].son[!c]].sz-2*t[t[z].son[!c]].sz>0。这样的话没有计算z，所以最后还要单独计算一下和z节点的异或值。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 using namespace std;
 const int maxn = 1e5 + ;

 int n, m, num, Log;
 int root[maxn], a[maxn], dep[maxn], p[maxn][];

 vector<int> G[maxn];

 struct Trie
 {
     int son[];
     int sz;
 }t[*maxn];

 void init(int x)
 {
     t[x].sz = ;
     memset(t[x].son,,sizeof(t[x].son));
 }

 void insert(int x, int y, int val)
 {
     x = root[x], y = root[y];
     for(int i=;i>=;i--)
     {
         int c = (val>>i)&;
         if(!t[x].son[c])
         {
             num++; init(num);
             t[x].son[c] = num;
             t[x].son[c^] = t[y].son[c^];
             t[t[x].son[c]].sz = t[t[y].son[c]].sz;
         }
         x = t[x].son[c], y = t[y].son[c];
         t[x].sz++;
     }
 }

 void dfs(int u, int fa)
 {
     num++; init(num);
     root[u] = num;
     p[u][] = fa;
     dep[u] = dep[fa]+;
     insert(u,fa,a[u]);
     for(int i=;i<G[u].size();i++)
     {
         int v = G[u][i];
         if(v==fa)  continue;
         dfs(v,u);
     }
 }

 void LCA_init()
 {
     for(int j=;j<=Log;j++)
         for(int i=;i<=n;i++)
         p[i][j] = p[p[i][j-]][j-];
 }

 int LCA(int x, int y)
 {
     if(x==y)  return x;
     if(dep[x]<dep[y])  swap(x,y);
     for(int i=Log;i>=;i--)
     {
         if(dep[p[x][i]] >= dep[y])  x=p[x][i];
     }
     if(x==y)  return x;
     for(int i=Log;i>=;i--)
     {
         if(p[x][i]!=p[y][i])  {x=p[x][i];y=p[y][i];}
     }
     return p[x][];
 }

 int query(int x, int y, int val)
 {
     int z = LCA(x,y);
     int tmp = a[z]^val;
     x = root[x], y = root[y], z = root[z];
     int ans = ;
     for(int i=;i>=;i--)
     {
         int c = (val>>i)&;
         if(t[t[x].son[!c]].sz+t[t[y].son[!c]].sz-*t[t[z].son[!c]].sz>)
         {
             ans+=(<<i);
             c^=;
         }
         x = t[x].son[c];
         y = t[y].son[c];
         z = t[z].son[c];
     }
     return max(ans,tmp);
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&m))
     {
         memset(p,,sizeof(p));
         memset(root,,sizeof(root));
         num = ; init();
         for(int i=;i<=n;i++)  {scanf("%d",&a[i]); G[i].clear();}
         for(int i=;i<=n-;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             G[u].push_back(v);
             G[v].push_back(u);
         }
         dep[] = ;
         dfs(,);

         n++;
         for(Log=;(<<Log)<=n;Log++);
         Log--;
         LCA_init();

         while(m--)
         {
             int x,y,z;
             scanf("%d%d%d",&x,&y,&z);
             printf("%d\n",query(x,y,z));
         }

     }
     return ;
 }