数据结构（C语言版）-第8章 排序

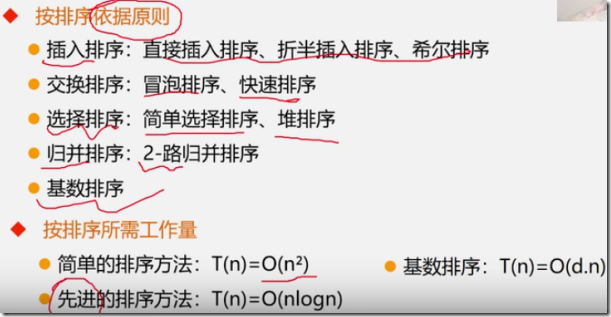
8.1　概述

1. 什么是排序？
  将一组杂乱无章的数据按一定规律顺次排列起来。

2. 排序的目的是什么？

——便于查找！

3. 什么叫内部排序？什么叫外部排序？

若待排序记录都在内存中，称为内部排序；

若待排序记录一部分在内存，一部分在外存，则称为外部排序。

注：外部排序时，要将数据分批调入内存来排序，中间结果还要及时放入外存，显然外部排序要复杂得多。

4.排序算法的好坏如何衡量？
时间效率——排序速度（比较次数与移动次数）
空间效率——占内存辅助空间的大小
稳定性——A和B的关键字相等，排序后A、B的先后次序保持不变，则称这种排序算法是稳定的。

# define MAXSIZE       //设记录不超过20个
typedef  int  KeyType ;     //设关键字为整型量（int型）

Typedef  struct {               //定义每个记录（数据元素）的结构
    KeyType      key ;            //关键字
    InfoType      otherinfo;   //其它数据项
}RedType ;

Typedef  struct {                       //定义顺序表的结构
  RedType  r [ MAXSIZE + ];   //存储顺序表的向量
                             //r[0]一般作哨兵或缓冲区
  int length ;       //顺序表的长度
}SqList ;

8.2　插入排序

每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。

即边插入边排序，保证子序列中随时都是排好序的

直接插入排序（基于顺序查找）

排序过程：整个排序过程为n-1趟插入，即先将序列中第1个记录看成是一个有序子序列，然后从第2个记录开始，逐个进行插入，直至整个序列有序。

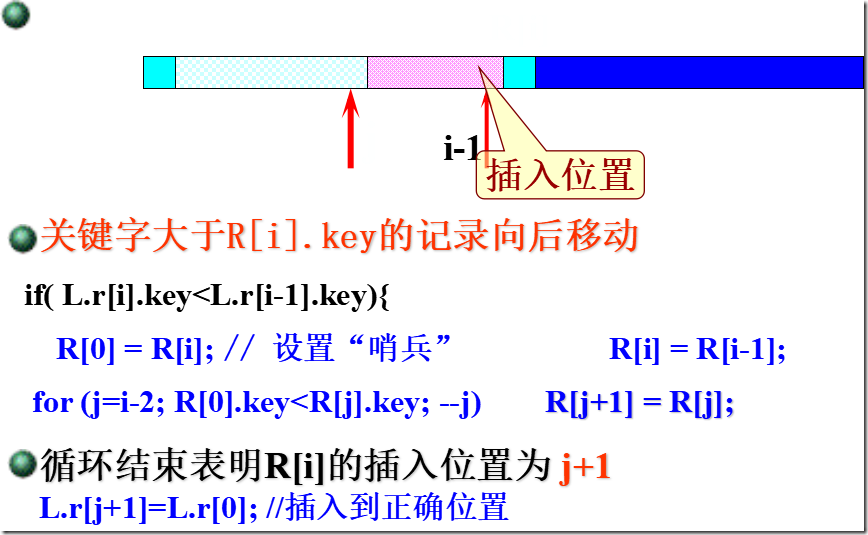
void InsertSort(SqList ＆L)
{int i,j;
   for(i=;i<=L.length;++i)
     if( L.r[i].key<L.r[i-].key)//将L.r[i]插入有序子表
       { L.r[]=L.r[i]; // 复制为哨兵
          L.r[i]=L.r[i-];
          for(j=i-; L.r[].key<L.r[j].key;--j)
                L.r[j+]=L.r[j]; // 记录后移
         L.r[j+]=L.r[]; //插入到正确位置
       }
}

最好情况下：
　每趟只需比较 1 次，不移动
　总比较次数为 n-1

最坏情况下：第 i 趟比较i次，移动i+1次

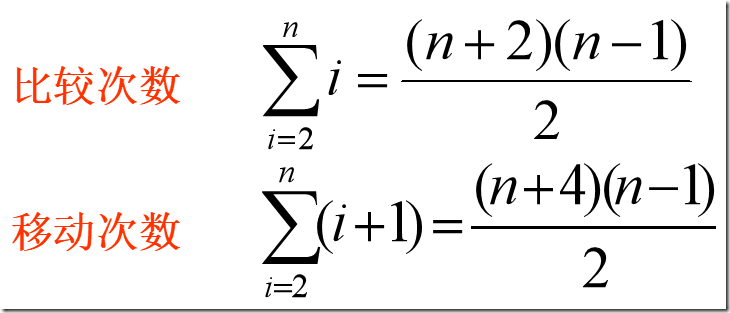
若出现各种可能排列的概率相同，则可取最好情况和最坏情况的平均情况
平均情况比较次数和移动次数为n2/4

时间复杂度为 o(n2)
空间复杂度为 o(1)
是一种稳定的排序方法

折半插入排序（基于折半查找）

减少关键字间的比较次数

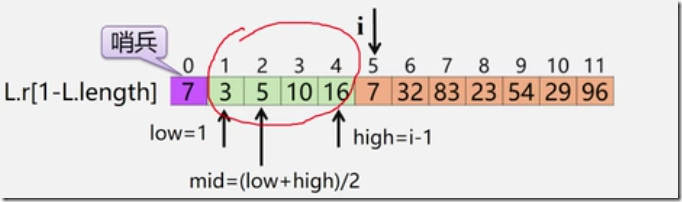
void  BInsertSort ( SqList &L )
{ for ( i = ;  i <= L.length ; ++i )
    {  L.r[] = L.r[i]; low =  ; high = i- ;
       while ( low <= high )
          {  m = ( low + high ) /  ;
             if  (  L.r[].key < L.r[m]. key  )  high = m - ;
            else  low = m + ;
           }
       for ( j=i-; j>=high+; - - j ) L.r[j+] = L.r[j];
       L.r[high+] = L.r[];
     }
  }  // BInsertSort

折半查找比顺序查找快，所以折半插入排序就平均性能来说比直接插入排序要快

它所需要的关键码比较次数与待排序对象序列的初始排列无关，仅依赖于对象个数。在插入第 i 个对象时，需要经过 log2i +1  次关键码比较，才能确定它应插入的位置

当 n 较大时，总关键码比较次数比直接插入排序的最坏情况要好得多，但比其最好情况要差
在对象的初始排列已经按关键码排好序或接近有序时，直接插入排序比折半插入排序执行的关键码比较次数要少
折半插入排序的对象移动次数与直接插入排序相同，依赖于对象的初始排列

减少了比较次数，但没有减少移动次数
平均性能优于直接插入排序

时间复杂度为 o(n²)
空间复杂度为 o(1)
是一种稳定的排序方法

希尔排序（基于逐趟缩小增量）

算法思想的出发点：

直接插入排序在基本有序时，效率较高
在待排序的记录个数较少时，效率较高

基本思想：

先将整个待排记录序列分割成若干子序列,分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

技巧：

子序列的构成不是简单地“逐段分割”
将相隔某个增量dk的记录组成一个子序列
让增量dk逐趟缩短（例如依次取5,3,1）
直到dk＝1为止。

优点：

小元素跳跃式前移
最后一趟增量为1时，序列已基本有序
平均性能优于直接插入排序

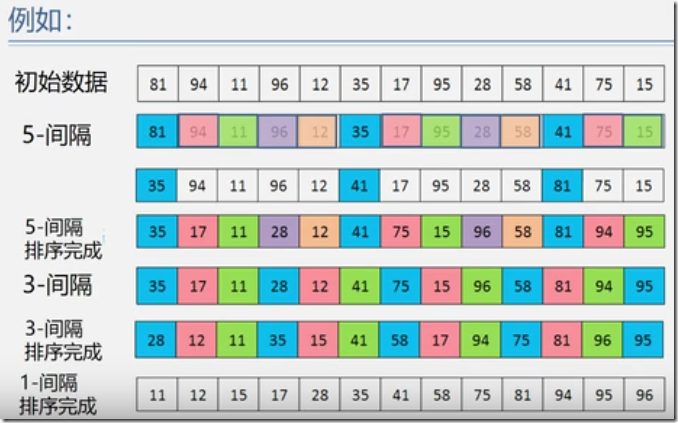
dk 值较大，子序列中对象较少，速度较快；
dk 值逐渐变小，子序列中对象变多，但大多数对象已基本有序，所以排序速度仍然很快。

void   ShellSort(SqList &L，int dlta[ ]，int t){
        //按增量序列dlta[0…t-1]对顺序表L作Shell排序
   for(k=；k<t；++k)
    　ShellInsert(L，dlta[k])；
　 　//增量为dlta[k]的一趟插入排序
}  // ShellSort

void   ShellInsert(SqList &L，int dk) {    //插入排序
 //对顺序表L进行一趟增量为dk的Shell排序，dk为步长因子
for(i=dk+；i<=L.length； ++ i)//开始将r[i] 插入有序增量子表
      if(r[i].key < r[i-dk].key) {
       r[]=r[i]；            //暂存在r[0]
       for(j=i-dk; j> &&(r[].key<r[j].key); j=j-dk)
          r[j+dk]=r[j]； //关键字较大的记录在子表中后移
        r[j+dk]=r[]；   //在本趟结束时将r[i]插入到正确位置
       }
}

8.3　交换排序

两两比较，如果发生逆序则交换，直到所有记录都排好序为止。

起泡排序O(n²)

基本思想：每趟不断将记录两两比较，并按“前小后大” 规则交换

优点：每趟结束时，不仅能挤出一个最大值到最后面位置，还能同时部分理顺其他元素；
           一旦下趟没有交换，还可提前结束排序

void main()
{    int a[];        /*a[0]不用，之用a[1]~a[10]*/
    int i,j,t;
    printf("\nInput 10 numbers: \n");
    for(i=;i<=;i++)    scanf("%d",&a[i]);    printf("\n");
    for(j=;j<=;j++)
        for(i=;i<=-j;i++)
          if(a[i]>a[i+])    {t=a[i];a[i]=a[i+];a[i+]=t;}//交换
    for(i=;i<=;i++)    printf("%d ",a[i]);
}

void bubble_sort(SqList &L)
{ int m,i,j,flag=;   RedType x;
   m=n-;
   while((m>)&&(flag==))
   {  flag

=

;
      for(j=;j<=m;j++)
         if(L.r[j].key>L.r[j+].key)
          {  flag=;
             x=L.r[j];L.r[j]=L.r[j+];L.r[j+]=x; //交换
           }//endif
      m--;
    }//endwhile
}

快速排序O( nlog₂n )

基本思想：
任取一个元素 (如第一个) 为中心
所有比它小的元素一律前放，比它大的元素一律后放，形成左右两个子表；
对各子表重新选择中心元素并依此规则调整，直到每个子表的元素只剩一个

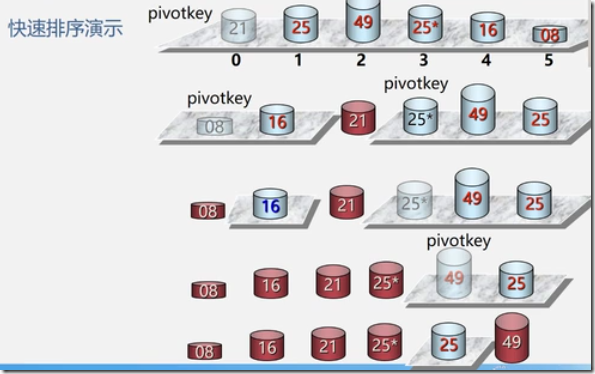
①每一趟的子表的形成是采用从两头向中间交替式逼近法；

②由于每趟中对各子表的操作都相似，可采用递归算法。

void main ( )
{   QSort ( L, , L.length ); }

void QSort ( SqList &L，int low,  int  high )
{  if  ( low < high )
    {  pivotloc = Partition(L, low, high ) ;
        Qsort (L, low, pivotloc-) ;
        Qsort (L, pivotloc+, high )
     }
}

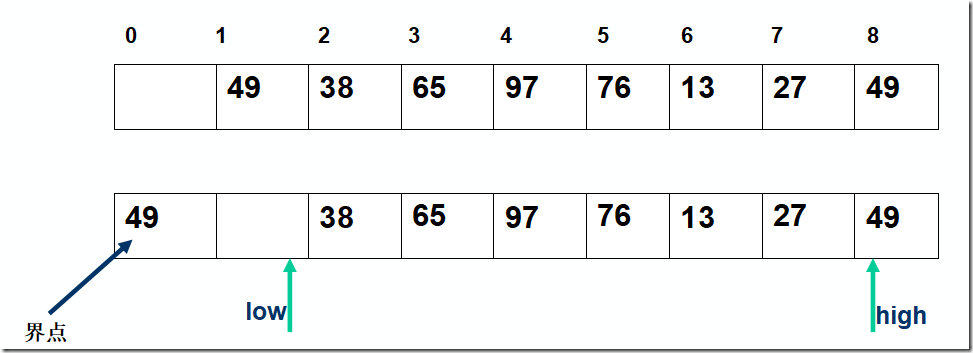
int Partition ( SqList &L，int low,  int  high )
{  L.r[] = L.r[low];   pivotkey = L.r[low].key;
   while  ( low < high )
    { while ( low < high && L.r[high].key >= pivotkey )  --high;
                 L.r[low] = L.r[high];
      while ( low < high && L.r[low].key <= pivotkey )  ++low;
                 L.r[high] = L.r[low];
     }
    L.r[low]=L.r[];
    return low;
}

https://www.bilibili.com/video/av38482542

算法分析：

可以证明，平均计算时间是O(nlog2n)。
实验结果表明：就平均计算时间而言，快速排序是我们所讨论的所有内排序方法中最好的一个。
快速排序是递归的，需要有一个栈存放每层递归调用时参数（新的low和high）。
最大递归调用层次数与递归树的深度一致，因此，要求存储开销为 O(log2n) 。

时间效率：O(nlog2n) —每趟确定的元素呈指数增加
空间效率：O（log2n）—递归要用到栈空间
稳 定 性： 不稳定   —可选任一元素为支点。

8.4　选择排序

简单选择排序

https://www.bilibili.com/video/av38482612

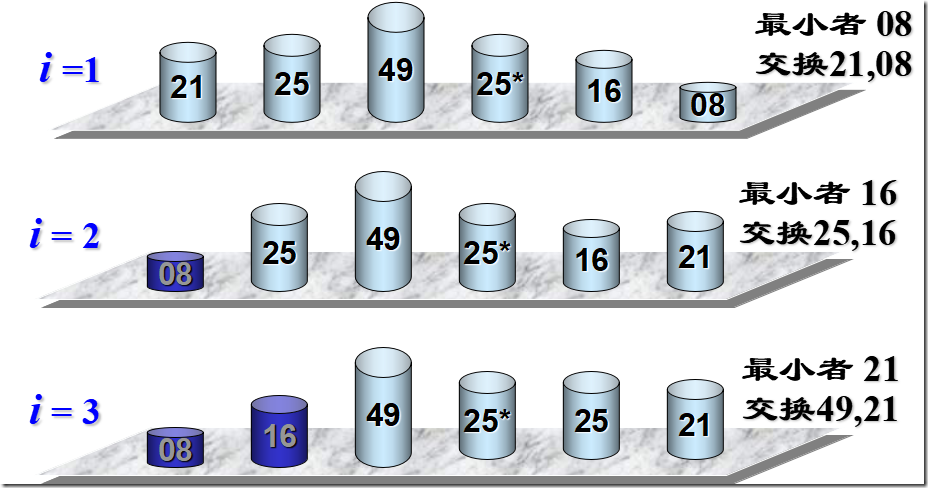
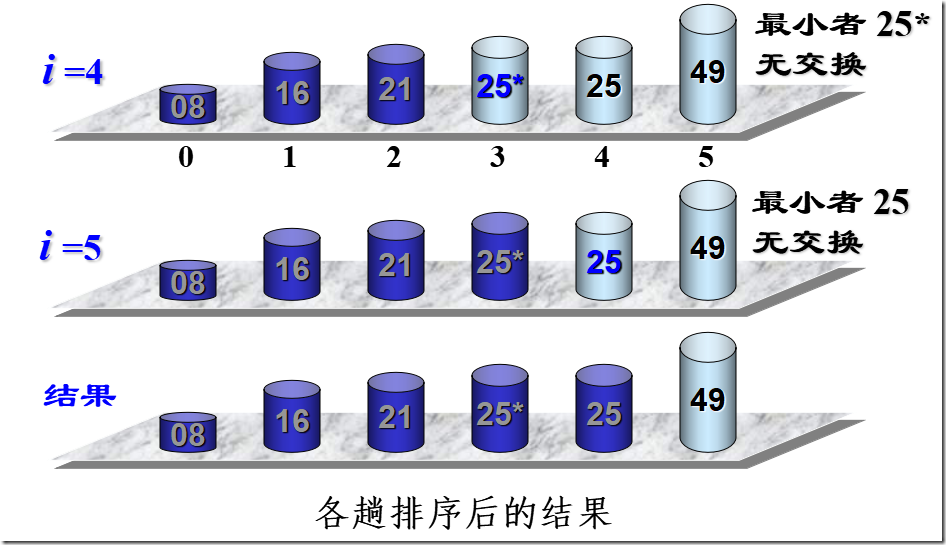
void SelectSort(SqList &K)
{
    for (i=; i<L.length; ++i)
    { //在L.r[i..L.length] 中选择key最小的记录
        k=i;
        for( j=i+;j<=L.length ; j++)
            if ( L.r[j].key <L.r[k].key) k=j;
        if(k!=i)L.r[i]←→L.r[k];
    }
}

时间复杂度：O(n²)
空间复杂度：O(1)
稳定

堆排序

https://www.bilibili.com/video/av38482686

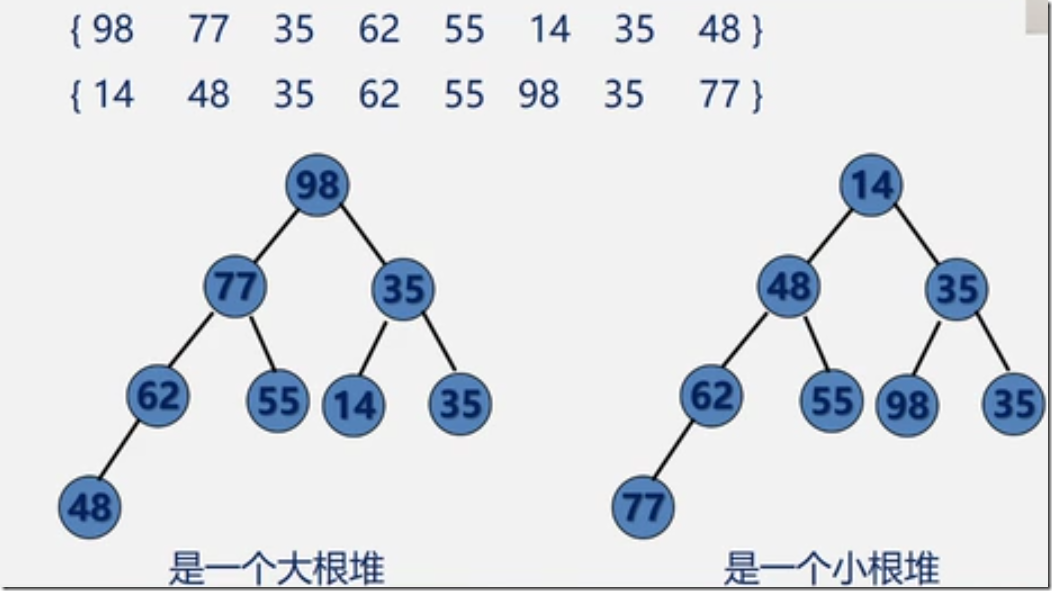
什么是堆？

n个元素的序列{k1,k2,…,kn}，当且仅当满足下列关系时，成为堆：

如果将序列看成一个完全二叉树，非终端结点的值均小于或大于左右子结点的值。

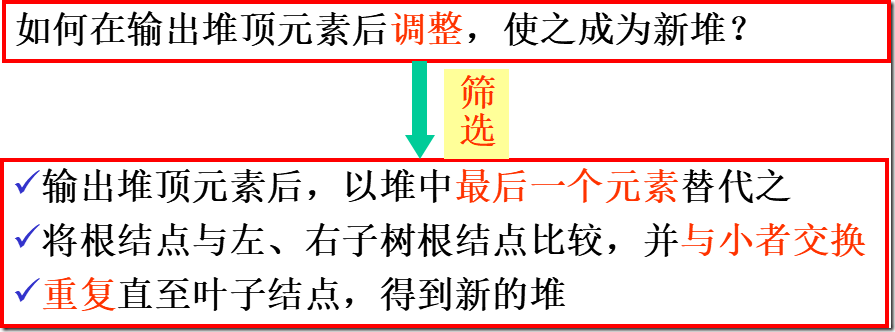
基本思想：

将无序序列建成一个堆
输出堆顶的最小（大）值
使剩余的n-1个元素又调整成一个堆，则可得到n个元素的次小值
重复执行，得到一个有序序列

时间效率：O(nlog2n)
空间效率：O（1）
稳 定 性：不稳定
适用于n 较大的情况

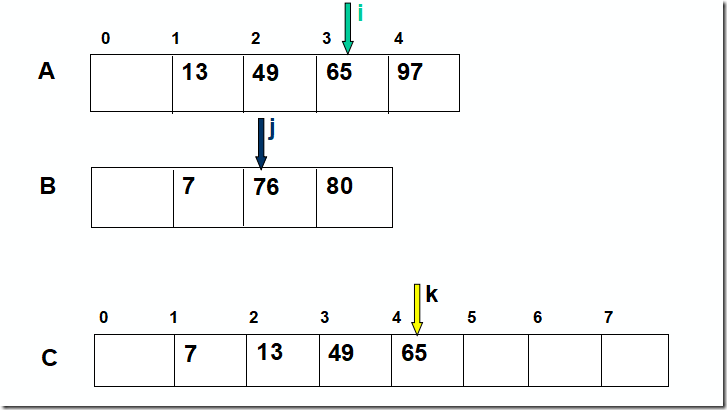
8.5　归并排序

https://www.bilibili.com/video/av38482791

归并：将两个或两个以上的有序表组合成一个新有序表

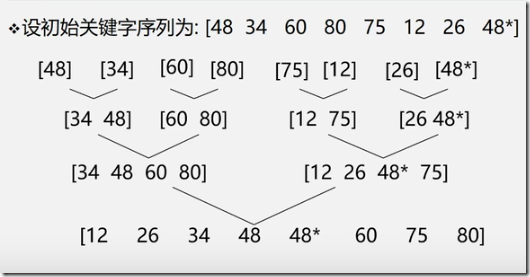
2-路归并排序

排序过程
初始序列看成n个有序子序列，每个子序列长度为1
两两合并，得到n/2个长度为2或1的有序子序列
再两两合并，重复直至得到一个长度为n的有序序列为止

时间效率：O(nlog2n)
空间效率：O（n）
稳 定 性：稳定

8.6　基数排序

8.6　外部排序

略

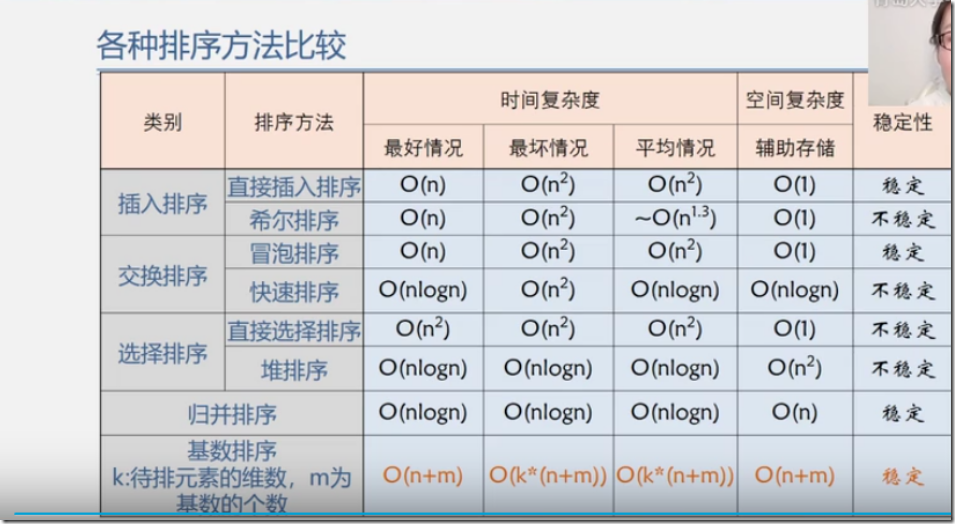
总结