图->连通性->最小生成树(克鲁斯卡尔算法)

文字描述

　　上一篇博客介绍了最小生成树(普里姆算法)，知道了普里姆算法求最小生成树的时间复杂度为n^2, 就是说复杂度与顶点数无关，而与弧的数量没有关系；

　　而用克鲁斯卡尔(Kruskal)算法求最小生成树则恰恰相反。它的时间复杂度为eloge (e为网中边的数目)，因此它相对于普里姆算法而言，适合于求边稀疏的网的最小生成树。

　　克鲁斯卡尔算法求最小生成树的步骤为：假设连通网N={V,{E}}, 则令最小生成树的初始状态为只有n个顶点而无边的非连通图 T=(V, {}}, 图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量中，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。依次类推，直至T中所有顶点都在同一连通分量上为止。

示意图：

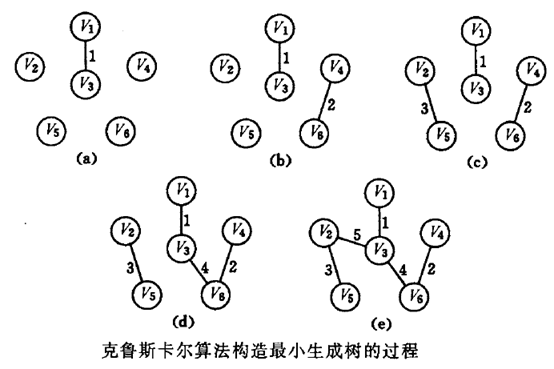
算法分析：

　　实现克鲁斯卡尔的话，可以借助于之前介绍的"堆"(堆排序)和树的等价划分的方法。用”堆”来存放网中的边，则每次选择最小代价的边仅需loge的时间(第一次需e)。又生成树T的每个连通分量可看成一个等价类，则构造T加入新的边的过程类似于求等价类的过程，由此可用MFSet类型来描述顶点，用堆Heap存放弧结点信息，使构造T的过程仅需eloge的时间，由此，克鲁斯

代码实现

 //
 // Created by lady on 18-12-15.
 //

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define MAX_NODE_NUM 20
 #define MAX_ARCH_NUM 30

 #define EQ(a, b) ((a)==(b))
 #define LT(a, b) ((a) <(b))
 #define LQ(a, b) ((a)<=(b))

 typedef struct PTNode{
     char data[];
     int index;
     int parent;
 }PTNode;

 typedef struct{
     PTNode node[MAX_NODE_NUM+];
     int n;
 }MFSet;

 typedef struct ArcBox{
     int vex1, vex2;
     int weight;
 }ArcBox;

 typedef  struct{
     ArcBox r[MAX_ARCH_NUM+];
     int len;
 }HeapType;

 /* param1 S: S是已存在的集合
  * param2 index: index是S中某个子集的成员的下标值
  * result: 查找函数，确定S中位置为index所属子集Si，并返回其子集中的根结点的位置。
  */
 static int findMFSet(MFSet *S, int index)
 {
     if(index <  || index > S->n)
         return -;
     int j = ;
     for(j=index; S->node[j].parent>; j=S->node[j].parent);
     return j;
 }

 /*
  * 集合S中位置为index_i和index_j所在的子集互不相交。
  * result: 将置为index_i和index_j所在的互不相交的子集合并为一个子集。
  */
 static int mergeMFSet(MFSet *S, int index_i, int index_j)
 {
     int loc_i = -, loc_j = -;
     if((loc_i=findMFSet(S, index_i)) < ){
         return -;
     }
     if((loc_j=findMFSet(S, index_j)) < ){
         return -;
     }
     if(loc_i == loc_j){
         return -;
     }
     //结点数少的子集指向结点数大的子集
     if(S->node[loc_i].parent > S->node[loc_j].parent){
         S->node[loc_j].parent += S->node[loc_i].parent;
         S->node[loc_i].parent = loc_j;
     }else{
         S->node[loc_i].parent += S->node[loc_j].parent;
         S->node[loc_j].parent = loc_i;
     }
     return ;
 }

 static int initialMFSet(MFSet *S, int n)
 {
     int i = ;
     S->n = n;
     for(i=; i<=S->n; i++)
     {
         printf("输入第%d个子集:", i);
         scanf("%s", S->node[i].data);
         S->node[i].parent = -;
         S->node[i].index = i;
     }
     return ;
 }

 /*
  * 返回结点中数据等于data的下标值
  */
 static int getLocaofVex(MFSet *S, char data[])
 {
     int i = ;
     for(i=; i<=S->n; i++){
         if(!strncasecmp(S->node[i].data, data, sizeof(S->node[].data))){
             return S->node[i].index;
         }
     }
     return -;
 }

 static void printMFSet(MFSet *S)
 {
     printf("打印MFSet结构中的数据:\n");
     int i = ;
     for(i=; i<=S->n; i++){
         printf("index %d:(data %s, parent %d)\n", S->node[i].index, S->node[i].data, S->node[i].parent);
     }
     printf("\n");
 }

 //////////////////////////////////////////////

 static int printHeap(HeapType *H)
 {
     printf("打印堆结构中的数据:\n");
     int i = ;
     for(i=; i<=H->len; i++){
         printf("index %d: arch:(%d,%d),weight %d)\n", i, H->r[i].vex1, H->r[i].vex2, H->r[i].weight);
     }
     return ;
 }

 static int initialHeap(HeapType *H, MFSet *S, int n)
 {
     H->len = n;
     int i = ;
     char s1[] = {};
     char s2[] = {};
     char s3[] = {};
     int weight = ;

     char tmp[] = {};
     for(i=; i<=H->len; i++)
     {
         printf("输入第%d条弧信息(顶点1 顶点2 权值)：", i);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%[^','],%[^','],%s[^\\n]", s1, s2, s3);
         H->r[i].vex1 = getLocaofVex(S, s1);
         H->r[i].vex2 = getLocaofVex(S, s2);
         H->r[i].weight = atoi(s3);
     }
     return ;
 }

 /*
  *已知H->r[s,...,m]中记录的关键字除H->r[s].key之外均满足的定义
  *本函数调整H-r[s]的关键字，使H->r[s,...,m]成为一个小顶堆(对其中
  *记录的弧的权值而言)
  */
 void HeapAdjust(HeapType *H, int s, int m)
 {
     ArcBox rc = H->r[s];
     int j = ;
     //沿weight较小的孩子结点向下筛选
     for(j=*s; j<=m; j*=){
         //j为weight较小的孩子结点下标
         if(j<m && (!LQ(H->r[j].weight, H->r[j+].weight)))
             j+=;
         if(LQ(rc.weight, H->r[j].weight))
             break;
         H->r[s] = H->r[j];
         s=j;
     }
     H->r[s] = rc;
 }

 void HeapSort(HeapType *H, MFSet *S)
 {
     int i = ;
     printf("1)建立一个小顶堆!\n");
     //把H->r[1,...,H->length]建成小顶堆
     for(i=H->len/; i>=; i--){
         HeapAdjust(H, i, H->len);
     }
     printHeap(H);
     printf("2)依次输出堆顶元素并重新调整成小顶堆!\n");
     ArcBox tmp;
     for(i=H->len; i>; i--){
         tmp = H->r[];
         H->r[] = H->r[i];
         H->r[i] = tmp;
         HeapAdjust(H, , i-);
         printf("新堆顶的弧信息: (%d,%d) %d", tmp.vex1, tmp.vex2, tmp.weight);
         if(mergeMFSet(S, tmp.vex1, tmp.vex2) > -){
             printf("\t是最小生成树的弧!\n");
         }else{
             printf("\n");
         }
     }
 }

 int main(int argc, char *argv[])
 {
     int nodes=;
     int archs=;
     printf("输入顶点数和弧数:");
     scanf("%d,%d", &nodes, &archs);

     printf("\n以MFSet结构存放顶点信息:\n");
     MFSet S;
     initialMFSet(&S, nodes);
     printMFSet(&S);

     printf("以堆结构存放弧信息:\n");
     HeapType H;
     initialHeap(&H, &S, archs);
     printHeap(&H);

     printf("对存放了弧信息的堆进行排序,在排序过程中输入最小生成树的边\n");
     HeapSort(&H, &S);
     return ;
 }

最小生成树(克鲁斯卡尔算法)

代码运行

/home/lady/CLionProjects/untitled/cmake-build-debug/untitled
输入顶点数和弧数:6,10

以MFSet结构存放顶点信息:
输入第1个子集:V1
输入第2个子集:V2
输入第3个子集:V3
输入第4个子集:V4
输入第5个子集:V5
输入第6个子集:V6
打印MFSet结构中的数据:
index 1:(data V1, parent -1)
index 2:(data V2, parent -1)
index 3:(data V3, parent -1)
index 4:(data V4, parent -1)
index 5:(data V5, parent -1)
index 6:(data V6, parent -1)

以堆结构存放弧信息:
输入第1条弧信息(顶点1 顶点2 权值)：V3,V1,1
输入第2条弧信息(顶点1 顶点2 权值)：V3,V2,5
输入第3条弧信息(顶点1 顶点2 权值)：V3,V5,6
输入第4条弧信息(顶点1 顶点2 权值)：V3,V6,4
输入第5条弧信息(顶点1 顶点2 权值)：V3,V4,5
输入第6条弧信息(顶点1 顶点2 权值)：V1,V2,6
输入第7条弧信息(顶点1 顶点2 权值)：V2,V5,3
输入第8条弧信息(顶点1 顶点2 权值)：V5,V6,6
输入第9条弧信息(顶点1 顶点2 权值)：V6,V4,2
输入第10条弧信息(顶点1 顶点2 权值)：V4,V1,5
打印堆结构中的数据:
index 1: arch:(3,1),weight 1)
index 2: arch:(3,2),weight 5)
index 3: arch:(3,5),weight 6)
index 4: arch:(3,6),weight 4)
index 5: arch:(3,4),weight 5)
index 6: arch:(1,2),weight 6)
index 7: arch:(2,5),weight 3)
index 8: arch:(5,6),weight 6)
index 9: arch:(6,4),weight 2)
index 10: arch:(4,1),weight 5)
对存放了弧信息的堆进行排序,在排序过程中输入最小生成树的边
1)建立一个小顶堆!
打印堆结构中的数据:
index 1: arch:(3,1),weight 1)
index 2: arch:(6,4),weight 2)
index 3: arch:(2,5),weight 3)
index 4: arch:(3,6),weight 4)
index 5: arch:(3,4),weight 5)
index 6: arch:(1,2),weight 6)
index 7: arch:(3,5),weight 6)
index 8: arch:(5,6),weight 6)
index 9: arch:(3,2),weight 5)
index 10: arch:(4,1),weight 5)
2)依次输出堆顶元素并重新调整成小顶堆!
新堆顶的弧信息: (3,1) 1    是最小生成树的弧!
新堆顶的弧信息: (6,4) 2    是最小生成树的弧!
新堆顶的弧信息: (2,5) 3    是最小生成树的弧!
新堆顶的弧信息: (3,6) 4    是最小生成树的弧!
新堆顶的弧信息: (4,1) 5
新堆顶的弧信息: (3,4) 5
新堆顶的弧信息: (3,2) 5    是最小生成树的弧!
新堆顶的弧信息: (5,6) 6
新堆顶的弧信息: (3,5) 6

Process finished with exit code 0