中文分词算法工具hanlp源码解析

词图

词图指的是句子中所有词可能构成的图。如果一个词A的下一个词可能是B的话，那么A和B之间具有一条路径E(A,B)。一个词可能有多个后续，同时也可能有多个前驱，它们构成的图我称作词图。

需要稀疏2维矩阵模型，以一个词的起始位置作为行，终止位置作为列，可以得到一个二维矩阵。例如：“他说的确实在理”这句话

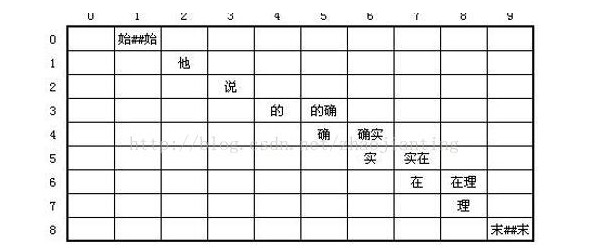
图词的存储方法：一种是的DynamicArray法，一种是快速offset法。Hanlp代码中采用的是第二种方法。

1、DynamicArray（二维数组）法

在词图中，行和列的关系：col为n 的列中所有词可以与row为n 的所有行中的词进行组合。例如“的确”这个词，它的col =5，需要和它计算平滑值的有两个，分别是row =5的两个词：“实”和“实在”。但是在遍历和插入的时候，需要一个个比较col和row的关系，复杂度是O(N)。

2、快速offset

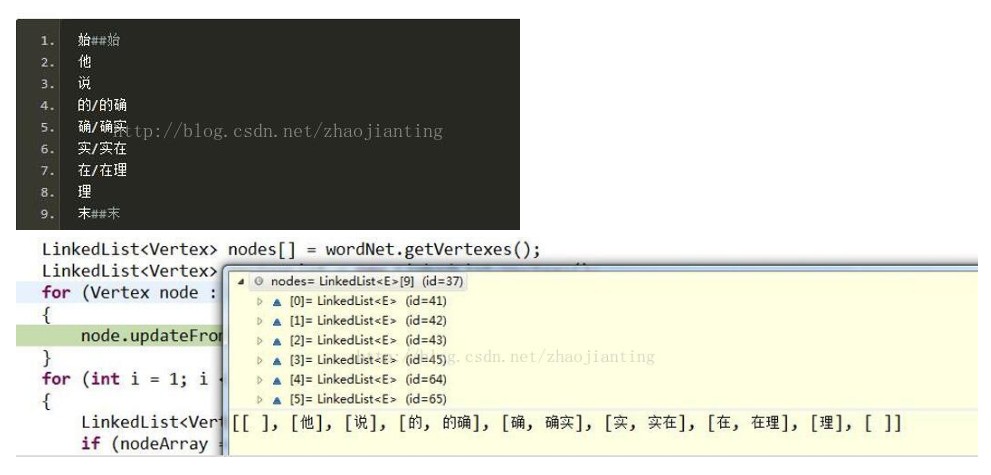
一个一维数组，每个元素是一个单链表“的确”的行号是4,长度是2,4+2=6，于是第六行的两个词“实/实在”就是“的确”的后续。

同时这种方法速度非常快，插入和查询的时间都是O(1)。

Hanlp核心词典：

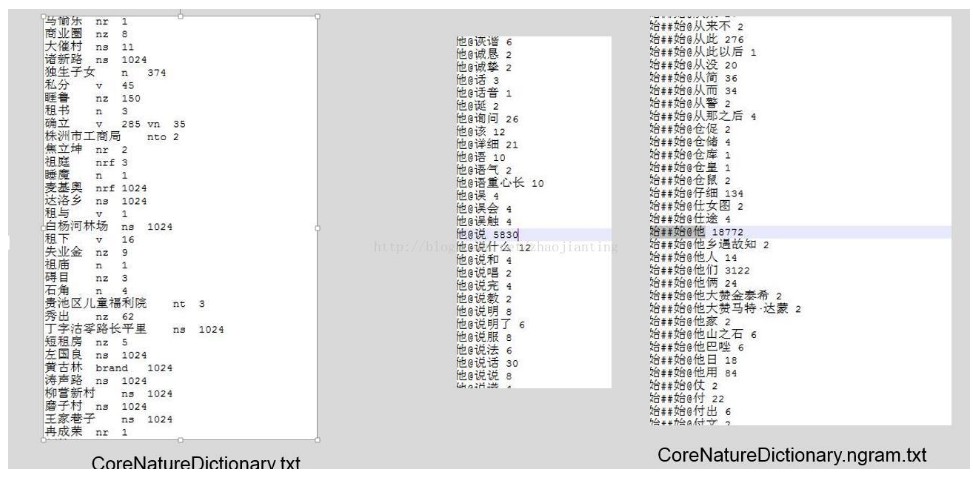
最短路径算法—viterbi（动态规划路径）

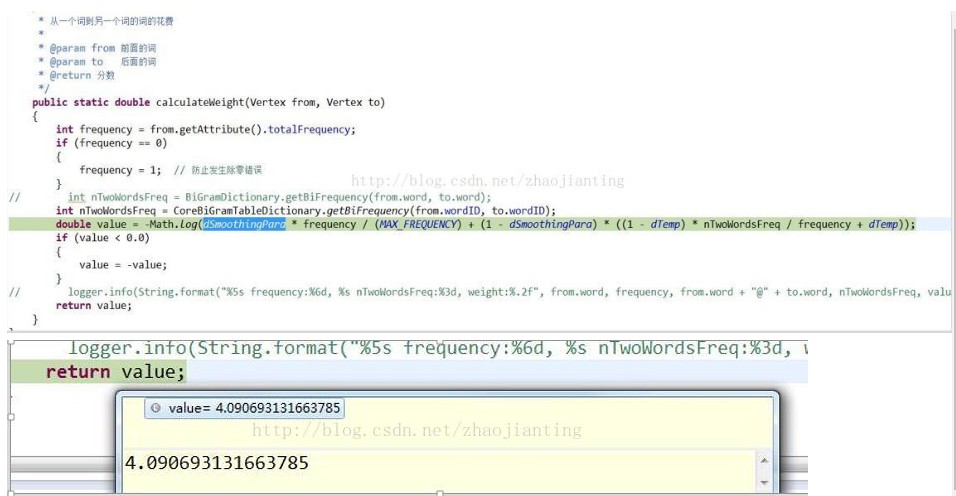
Frequency:核心词典中的词频

nTwoWordsFreq:共现词频

intMAX_FREQUENCY= 25146057

double dTemp =(double) 1 / MAX_FREQUENCY +0.00001

dSmoothingPara =0.1

Viterbi最短路径有向图

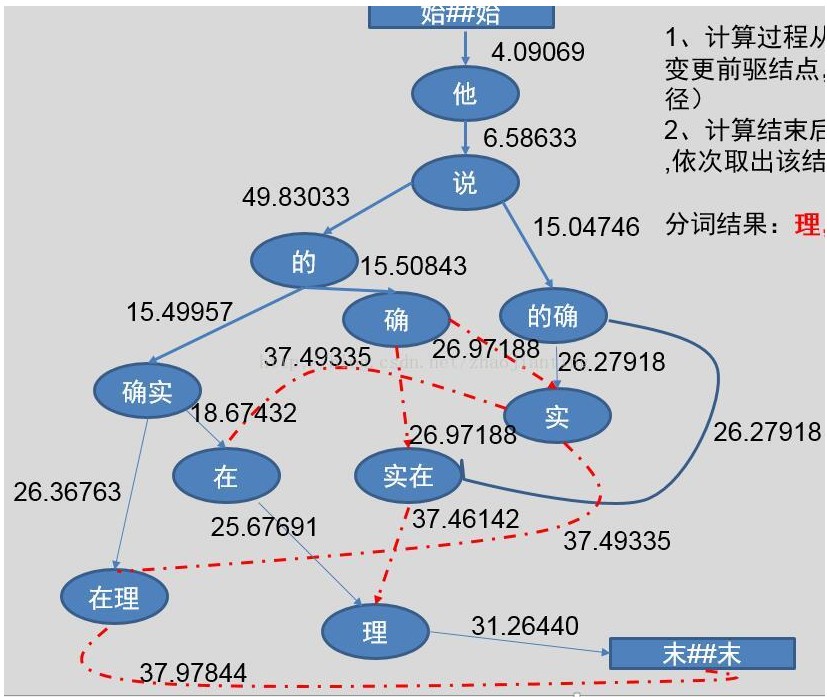
1、计算过程从上至下，根据计算出的权重值变更前驱结点，保证前驱结点唯一（动态规划路径）

2、计算结束后，从最后一个结点开始取出term,依次取出该结点的前驱结点即可分词结果：理，在，确实，的，说，他