51nod1237 最大公约数之和 V3

题意：求

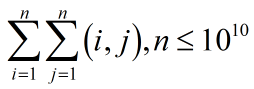
解：

最后一步转化是因为phi * I = Id，故Id * miu = phi

第二步是反演，中间省略了几步...

然后就这样A了......最终式子是个整除分块，后面用杜教筛求一下phi前缀和即可。

 #include <cstdio>
 #include <map>

 typedef long long LL;
 const int N = , T = ;
 const LL MO = ;

 int p[N], top, phi[N];
 LL Phi[N], inv2;
 bool vis[N];
 std::map<LL, LL> mp;

 inline void getp(int n) {
     phi[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             phi[i] = i - ;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             if(i % p[j] == ) {
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
         }
     }
     for(int i = ; i <= n; i++) {
         Phi[i] = (Phi[i - ] + phi[i]) % MO;
     }
     return;
 }

 LL getPhi(LL x) {
     if(x <= ) return ;
     if(x <= T) return Phi[x];
     if(mp.count(x)) return mp[x];
     LL ans = (x + ) % MO * (x % MO) % MO * inv2 % MO;
     for(LL i = , j; i <= x; i = j + ) {
         j = x / (x / i);
         ans -= (j - i + ) % MO * getPhi(x / i) % MO;
         ans %= MO;
     }
     return mp[x] = (ans + MO) % MO;
 }

 int main() {
     LL n;
     getp(T);
     inv2 = (MO + ) / ;
     scanf("%lld", &n);
     LL ans = ;
     for(LL i = , j; i <= n; i = j + ) {
         j = n / (n / i);
         LL temp = (n / i) % MO;
         ans += temp * temp % MO * (getPhi(j) - getPhi(i - ) + MO) % MO;
         ans %= MO;
     }
     printf("%lld\n", (ans + MO) % MO);
     return ;
 }

AC代码