[FJOI2017]矩阵填数——容斥

参考：题解 P3813 【[FJOI2017]矩阵填数】

题目大意：

给定一个 h∗w 的矩阵,矩阵的行编号从上到下依次为 1...h ，列编号从左到右依次 1...w 。

在这个矩阵中你需要在每个格子中填入 1...m 中的某个数。

给这个矩阵填数的时候有一些限制，给定 n个该矩阵的子矩阵,以及该子矩阵的最大值 v ,要求你所填的方案满足该子矩阵的最大值为 v 。

现在,你的任务是求出有多少种填数的方案满足 n 个限制。

两种方案是不一样的当且仅当两个方案至少存在一个格子上有不同的数。由于答案可能很大，你只需要输出答案 mod 1,000,000,007

分析：

首先我们可以发现，处理的时候，应该将所有矩阵按照v的大小升序排列，因为，当两个矩阵范围产生交集的时候，交集处必然要填充小的v。

所以，我们先填v小的，再填v大的，每一个矩阵的面积，都是与之前所有的矩形取并后的面积，再减去之前所有矩形的面积。

也就是，选择之前没有被覆盖的矩形面积。

方案数就是：利用乘法原理，每个矩形处理后，ans加上v的面积次方？

NAIVE！

这些个值，每一个都是所有的方案数，不一定每一个方案数都有一个数能等于最大值v.也就是说可能取不到最大值.

那方案数就是：每个矩形处理后，ans加上：v的面积次方，再减去(v-1)的面积次方？（这就去除不合法解了)

N!A!I!V!E!

我们必须要考虑到这样一种情况：

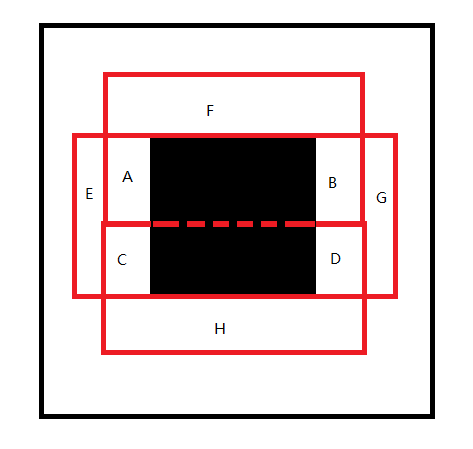
图中，一共有4个子矩形，其中，三个红色矩形v值相同，假设都为3，黑色矩形v是2，根据计划，刚才已经处理完了。

这个时候，假设我们要处理上面的这个矩形（F所在矩形）会把A+B+F作为剩下的面积进行统计，加入ans。

之后，假设我们要处理中间的矩形（E、G所在矩形）剩下的面积E+C+D+G作为统计。

按照刚才的做法和分析，这些方案都是合法的。

但是我们漏了一种情况：

当A点有v值的时候，因为，上面、中间的矩形要求的最大值相同，所以，A有了v，E、C、D、G区间已经可以瞎选了！！但是这些方案我们没有考虑到。

也就是说，在矩形v相同的时候，且有交集的时候，在交集的地方，会出现一石二鸟，bug。

所以v相同的矩形，必须当做一个大的集合考虑！！

发现，交集这种东西很难考虑。

这个图挺眼熟，像Venn图。

那就用容斥吧。

我们先把所有的可能方案数算出来v^(A+...+H)

有一些方案数，中间矩阵不满足取最大值。减去v^(F+H)*(v-1)^(A+B+C+D+E+G)

一些方案数，上边矩阵不能满足。同理减去。

下边矩阵……

。。。。

但是，中间矩阵，上边矩阵同时不能选（交集）的方案数减了两遍，再加上一遍：交集部分选不了最大值的方案数。

。。。。

以此类推。

具体步骤：

0.输入，排序

1.处理交集

2.处理并集 (利用交集做容斥)

3.按值相同的一组处理

实现其实挺不好写的。状压写的还是少。（蒟蒻）所以参考了题解。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=;
const int M=;
const int mod=1e9+;
ll s[M],u[M];
int siz[M];
int n,m,w,h,t;
ll ans;
inline ll qm(ll x,ll y){
    ll ret=,base=x;
    while(y){
        if(y&) ret=(ret*base)%mod;base=(base*base)%mod;y>>=;
    }
    return ret;
}//快速幂
struct node{
    ll x1,x2,y1,y2;
    int v;
    inline void rd(){
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&v);
    }
    inline bool ck(){return (x1>x2)||(y1>y2);}//判断空矩阵
    inline ll calc(){return (x2-x1+)*(y2-y1+);}
    void operator &=(const node & a)//两个矩阵求交集
    {
        x1=max(x1,a.x1);y1=max(y1,a.y1);
        x2=min(x2,a.x2);y2=min(y2,a.y2);
    }
    friend bool operator <(node a,node b)
    {
        return a.v<b.v;
    }
}ju[N],tr;//矩阵
void clear()
{
    ans=;
    memset(s,,sizeof s);
    memset(u,,sizeof u);
}
void work()
{
    int up=(<<n)-;//全集
    for(int i=;i<=up;i++)//交集
    {
        tr.x1=,tr.y1=,tr.x2=h,tr.y2=w;
        bool flag=true;
        for(int j=;j<=n;j++)
        {
            if((<<(j-))&i)
            {
                tr&=ju[j];
                if(tr.ck()){
                    flag=false;break;
                }
            }
        }
        if(flag) s[i]=tr.calc();//s[i],i集合所交集的面积
    }
    for(int i=;i<=up;i++)//并集
    {
        ll sum=;
        for(int j=i;j;j=(j-)&i)
        {
            if(siz[j]%==)
            {
                sum+=s[j];
            }
            else sum-=s[j];
        }//容斥求i集合的并集面积
        u[i]=sum;
    }
    ll ns=,la=;
    ll ret=;
    for(int i=;i<=n;i++)
    {
        ns|=(<<(i-));if(ju[i].v==ju[i+].v) continue;//取出所有v相等的矩阵，作为一个集合
        ll sheng=u[ns|la]-u[la];//总剩余面积
        ret=qm(ju[i].v,sheng);//初始方案数
        for(int j=ns;j;j=(j-)&ns)//枚举子集，做容斥
        {
            ll now=u[j|la]-u[la];
            ll kk=(qm(ju[i].v-,now)*qm(ju[i].v,sheng-now))%mod;
            if(siz[j]%==)
            {
                ret=(ret+mod-kk)%mod;
            }
            else ret=(ret+kk)%mod;
        }
        la|=ns,ns=;//la，之前所有取过的矩阵集合
        ans=ans*ret%mod;
    }
    ans=ans*qm(m,h*w-u[la])%mod;//别忘了，除子矩阵外的面积也有方案数，可以随便取
    printf("%lld\n",ans);
}
int main()
{
    scanf("%d",&t);
    for(int i=;i<=;i++)
     siz[i]=siz[i>>]+(i&);//size[i] i的二进制中1的个数
    while(t)
    {
        scanf("%d%d%d%d",&h,&w,&m,&n);
        for(int i=;i<=n;i++) ju[i].rd();
        sort(ju+,ju+n+);
        ans=;
        work();
        clear();
        t--;
    }
    return ;
}