NOIP2018提高组初赛知识点

 （传说，在神秘的初赛中，选手们经常互相爆零以示友好……）

历年真题：ti.luogu.com.cn

以下标题中打*的是我认为的重点内容

一、关于计算机

（一）计算机组成

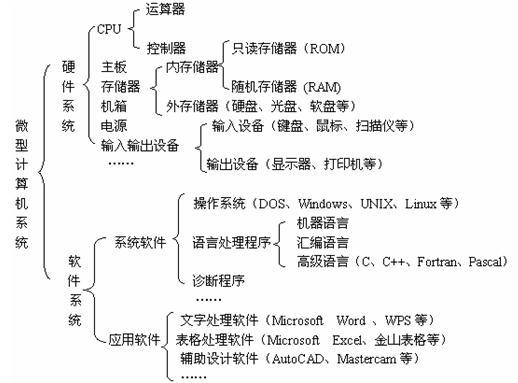
硬件组成：

1. 控制器(Control):是整个计算机的中枢神经，其功能是对程序规定的控制信息进行解释，根据其要求进行控制，调度程序、数据、地址，协调计算机各部分工作及内存与外设的访问等。

2. 运算器(Datapath):运算器的功能是对数据进行各种算术运算和逻辑运算，即对数据进行加工处理。

3. 存储器(Memory):存储器的功能是存储程序、数据和各种信号、命令等信息，并在需要时提供这些信息。

4. 输入(Input system):输入设备是计算机的重要组成部分，输入设备与输出设备合称为外部设备，简称外设，输入设备的作用是将程序、原始数据、文字、字符、控制命令或现场采集的数据等信息输入到计算机。常见的输入设备有键盘、鼠标器、光电输入机、磁带机、磁盘机、光盘机等。

5. 输出(Output system):输出设备与输入设备同样是计算机的重要组成部分，它把外算机的中间结果或最后结果、机内的各种数据符号及文字或各种控制信号等信息输出出来。微机常用的输出设备有显示终端CRT、打印机、激光印字机、绘图仪及磁带、光盘机等。

【CPU（中央处理器）=运算器+控制器+寄存器

存储器=内存储器+外存储器】

​BIOS是英文"Basic Input Output System"的缩略语，直译过来后中文名称就是"基本输入输出系统"。其实，它是一组固化到计算机内主板上一个ROM芯片上的程序，它保存着计算机最重要的基本输入输出的程序、系统设置信息、开机后自检程序和系统自启动程序。 其主要功能是为计算机提供最底层的、最直接的硬件设置和控制。

随机存储器RAM的“随机”指“随时访问”

断电后可以保存数据：硬盘，ROM

断电后不可以保存数据：显存（显卡内存），RAM，CPU

面向过程语言 ：C

面对对象的高级语言：C++，Java

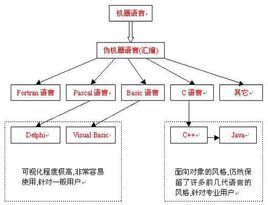
（二）计算机发展史

（这部分中部分内容参考洛谷日报第45期。感谢）

（三）计算机中各存储单位的进位关系：
1TB=1024GB，1GB=1024MB，1MB=1024KB
1KB=1024B，1B（字节）=8bit（位）

二、二进制原码、反码与补码

（这部分中部分内容参考https://blog.csdn.net/jq_ak47/article/details/45338061。感谢）

（一）原码

在计算机中（以八位机为例），我们知道都用二进制来存储数

如5，二进制为00000101

那么负数怎么存储？将最高位设为符号位，正数为0，负数为1

如-5，二进制为10000101

-6，为10000110

以上叫做原码

（二）反码

反码表示法规定：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

如7，原码为00000111，反码为00000111

如-10，原码为10001010，反码为11110101

（三）补码

正数的补码是其本身，负数的补码是反码加一

补码有什么用呢？解决负整数加减法

比如我们计算16-8 或是 16+（-8）

如果用原码计算

0 0 0 0 1 0 0 0

+1 0 0 0 0 1 0 0

————————

1 0 0 0 1 1 1 1

将10001111转换为二进制，结果为-24，显然不对

如果用补码呢？

0 0 0 0 1 0 0 0

+ 1 1 1 1 1 1 0 0

————————

1 0 0 0 0 0 1 0 0

*注意，此处用八位二进制，而计算结果是九位二进制，所以最高位自动省略

这样结果是-8，正确

若要将补码转化为原码，正数不变，负数先-1再取反码就可以了

三、P问题、NP问题与NPC问题

（这部分中部分内容参考http://www.matrix67.com/blog/archives/105。感谢）

我就说的简略一点了（主要是怕自己忘了），详见上面网址

（一）P问题

每个问题的算法都有时间复杂度

O(1),O(N),O(NlogN),O(n²)等n不在指数为的复杂度为多项式级复杂度

O(N!),O(2ⁿ）等复杂度是非多项式级的

可以找到一个多项式级复杂度算法的问题是P问题

NOI系列考的绝大多数问题都是P问题

注：如果一个问题不存在多项式空间的算法，那它一定不是 P 类问题（详见NOIP2012提高组初赛第20题）

（二）NP问题

一个解可以用多项式级复杂度检验的问题是NP问题

注：找不到多项式复杂度解的(非P问题)不一定是NP问题

易得NP=P。即所有P问题都是NP问题

至于P=NP，大家感兴趣的话可以自己研究研究（滑稽护体）

（三）NPC问题（NP-完全问题）

先讲一下“约化”

有两个问题，问题A和问题B

若可以用问题B的算法来解决问题A，那么问题A可以约化为问题B

比如，一元一次方程可以约化为一元二次方程

约化具有传递性，即A可以约化成B，B可以约化成C，那么A一定可以约化成C

可以看出，在不断约化的过程中，算法的时间复杂度逐渐增高，解决的问题也越来越广

大胆猜测，是否可以将所有的NP问题都约化成一个问题？解决了这个问题就能解决所有NP问题？

答案是肯定的！

而且这不仅是一个问题，还是一类问题

这类问题叫做NPC问题。

一个问题满足以下两条，它就是NPC问题：

1、它是NP问题

2、所有的NP问题都可以约化到它

NPC问题的鼻祖是逻辑电路问题，有兴趣的读者可以自行了解。

另外说一下NP-hard问题，它满足NPC问题的第二条但不满足第一条。它的范围比NPC问题广。

*四、进制转换

（一）二、四、八、十六互转通用方法：

以八进制转二进制为例

先把关系表列出来：

八进制数	二进制数
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

二转八：

例如：10010011.1011

2^3=8

所以使用三位一合的方法。若整数部分位数不是三的倍数，在最高位前补0；若小数部分位数不是三的倍数，在末尾补0。接着以小数点为分界，从左到右分别转化小数部分和整数部分。

对照上面的表 10 010 011. 101 100

2   2      3 .   5     4

所以(10010011.1011)₂=(223.54)₈

八转二：

同理，一位三分法

例如：7643

对照上面的表 7    6      4     3

111  110  100  011

注：十六进制等进制中，A代表10，B代表11，以此类推

（二） 二转十和十转二

二转十：个位*2^0，十位*2^1，百位*2^2…… 若是小数，十分位*2^-1，百分位*2^-2……然后加起来就行了

十转二：整数部分：不断除以2，直到商为0，倒取各阶段余数

小数部分：不断乘以2，直到积为1，正取各阶段整数

如10.25转化为二进制

10÷2=5……0

5÷2=2……1

2÷2=1……0

1÷2=0……1

倒着取余数，1010即为整数部分

0.25*2=0.5……0

0.5*2=1……1

正着取整数，0.01即为小数部分

将两部分合起来，得到10.25=(1010.01)₂

（三）其它

其它2^n的进制如要转化为十进制，先转化为二进制，再转化为十进制。

十进制转化成它们同理。

**五、排序算法

基本是每年必考！

（这部分中部分内容参考http://blog.csdn.net/whuslei/article/details/6442755/ 和 https://blog.csdn.net/xiazdong/article/details/8462393。感谢）

九大排序算法：（加上桶排序就是十个）

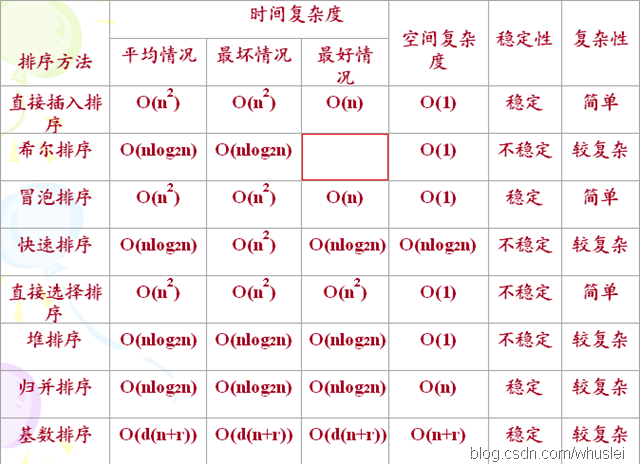
计数排序            O(N+K)             O(N+K)               O(N+K)           O(n+K)          稳定             简单

排序算法稳定，指排序前后数值相同的两个数相对位置不会改变

稳定：插、归、冒、基、计

不稳定：快、堆、希、选

需要额外空间：归、基、计

不需要额外空间：插、希、冒、快、堆、选

运用分治思想的：归、快

时间复杂度是O(NlogN)的：堆、快、归（希尔排序的时间复杂度依赖于增量的选择，这里不做讨论）

最慢是O(N²)的：插、冒、快、选

最快是O(N)的：插、冒（改进后）

最快最慢相同的：冒（不改进）、选、堆、归、基，计

注意：近些年题目考的越来越“活”了，千万不要死记硬背！

example：（NOIP2017提高组）

11.设 A 和 B 是两个长为 n 的有序数组，现在需要将 A 和 B 合并成一个排好序的 数组，请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 （ ）次比较。

[黑人问号.jpg]

答案：2n-1

六、时空复杂度

（一）时间复杂度

（这部分中部分内容参考https://www.luogu.org/blog/Chanis/master。感谢 ）

表的第二行是一些奇怪的东西，不用管它

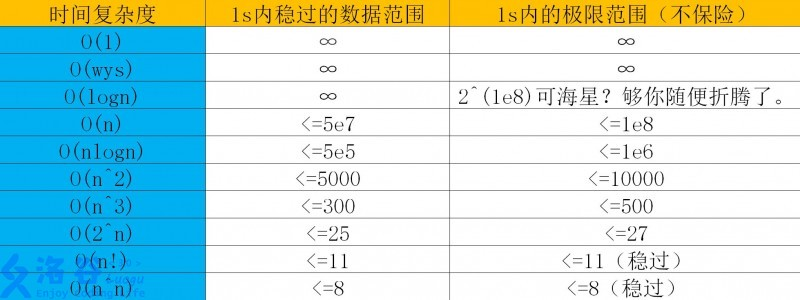
初赛还经常要计算代码的时间复杂度。对于递归函数的一定要细心思考

（二）空间复杂度

（这部分中部分内容参考https://blog.csdn.net/shiwei408/article/details/7280296?utm_source=copy 。感谢）

32位系统下，int、long、long long、__int64所占字节数（B）
char: 1字节（8位）
int: 4字节 (32位，取值范围 -2^31 ～ 2^31-1)
unsigned int : 4字节 (32位，取值范围 0 ～ 2^32-1)
long: 4字节 (32位，取值范围 -2^31 ～ 2^31-1)
unsigned long : 4字节 (32位，取值范围 0 ～ 2^32-1)
long long : 8字节(64位，取值范围 -2^63 ～ 2^63-1)

七、位运算与逻辑运算 

（一）位运算

按位与：&

按位或：|

按位异或：^

按位取反：~（对于十进制来说，取相反数再减一）

左移：<<

右移：>>

*优先级：~大于>>、<<大于&大于^大于|大于&=、^=、|=、<<=、>>=

（二）逻辑运算

"∨" 表示"或" (逻辑加法)

"∧" 表示"与". (逻辑乘法)

"┐"表示"非". (逻辑否定)

"⊕"表示"异或"

按位运算优先级大于逻辑运算

与：11为1，其它为0

或：00为0，其它为1

异或：不同为1，相同为0

八、指针

一个小东西……不过易混淆！

int a;//定义一个变量

int *p;//定义一个指针

*p=&a;//指针p取到a的地址（p是一个地址）

cout<<*p;//输出地址中的值（*p是一个值）

example：NOIP2015提高组第24题

#include <iostream>
using namespace std;
void fun(char *a, char *b) {
    a = b; //a变为c2的地址。注意，指针=指针时地址中的值不变，变的只是指针
    (*a)++; //将a地址（c2）中的值+1
}
int main() {
    char c1, c2, *p1, *p2;
    c1 = 'A';
    c2 = 'a';
    p1 = &c1; //p1是c1的地址
    p2 = &c2; //p2是c2的地址
    fun(p1, p2); //（NOIP的函数好像都叫fun……）
    cout << c1 << c2 << endl;//输出为Ab
    return ;
} 

*九、图论（只讲一点点）

图论挺重要的，板子需要背一背

下面只是一些概念

（一）无向图

完全图：n 个点，n(n-1)/2 条边（每对顶点之间都恰连有一条边）

树：n 个点，n-1 条边（每对顶点之间都有且仅有一条路径，无环）

割点：删除该点后图不连通

割边（桥）：删除该边后图不连通

点双连通：某个没有割点的无向图

边双连通：某个没有割边（桥）的无向图

双连通分量：图的极大双连通子图（分为点双连通分量和边双联通分量）

（二）有向图

强连通：在有向图G中，若u能到v，v也能到u，则称u和v是强连通的

强连通图：若有向图G的任意两个节点都强连通，则称G是一个强连通图

强连通分量：有向非强连通图的极大强连通子图，称为强连通分量

DAG：有向无环图

将一个有向图中的强连通分量都缩成一个点，则原图会形成一个DAG

拓扑排序仅适用于DAG

十、计算机奖项

（这部分中部分内容参考https://blog.csdn.net/qq_39992190/article/details/78160251?utm_source=copy。感谢）

图灵奖 (A.M. Turing Award) 由ACM于1966年设立
“计算机界的诺贝尔奖”
奖励那些对计算机事业做出重要贡献的个人

约翰•冯•诺依曼奖 由IEEE（电气和电子工程师协会）于1990年成立
表扬在计算机科学和技术上具有杰出成就的科学家

高德纳奖 (Donald E. Knuth Prize) 始于1996 1.5年颁发一次
授予为计算机科学基础做出杰出贡献的人

……

二一四七四八三六四七、一些杂乱的

（一）根据国际信息学奥林匹克竞赛（IOI）的相关决议并考虑到我国目前程序设计语言的具体情况，CCF决定：1.2020年开始，除NOIP以外的NOI系列其他赛事（包括冬令营、CTSC、APIO、NOI）将不再支持Pascal语言和C语言；2.从2022年开始，NOIP竞赛也将不再支持Pascal语言。即从NOIP2022开始，NOI系列的所有赛事将全部取消Pascal语言。在无新增程序设计语言的情况下，NOI系列赛事自NOIP2022开始将仅支持C++语言。（NOIP2017提高组第一题）

（二）IP地址是一个32位的二进制数，通常被分割为4个“8位二进制数”（也就是4个字节）。IP地址通常用“点分十进制”表示成（a.b.c.d）的形式，其中，a,b,c,d都是0~255之间的十进制整数。例：点分十进IP地址（100.4.5.6），实际上是32位二进制数（01100100.00000100.00000101.00000110）。

（三）哈夫曼编码采用贪心思想。该方法完全依据字符出现概率来构造异字头的平均长度最短的码字。哈夫曼树的叶子节点个数比非叶子节点个数多一。

（四）编译器的主要功能是将源程序翻译成指令

（五）字串是连续的，但子序列不一定是连续的

祝所有参赛选手rp++,score++,luck++！！！

本文部分图片来源于网络

若需转载，请注明https://www.cnblogs.com/llllllpppppp/p/9749930.html