BZOJ.4453.cys就是要拿英魂！(后缀数组 单调栈)

BZOJ

求字典序最大，容易想到对原串建后缀数组求\(rk\)。

假设当前区间是\([l,r]\)，对于在\([l,r]\)中的两个后缀\(i,j\)（\(i<j\)），显然我们不能直接比较\(rk_i,rk_j\)来比较\(i,j\)在\([l,r]\)中谁的字典序更大。（比如对于串\(babb\)，\(l=1,r=3\)，在原串中，后缀\(3(bb)\)的排名比\(1(babb)\)靠后，但是在\([1,3]\)中显然应该是\(1\)的字典序更大）

但还是可以讨论一下：

• 若\(rk_i>rk_j\)，\(i\)在\([l,r]\)中的字典序一定比\(j\)大。
• 若\(rk_i<rk_j\)，且\(LCP(i,j)<r-j+1\)，\(j\)在\([l,r]\)中的字典序一定比\(i\)大。
• 若\(rk_i<rk_j\)，且\(LCP(i,j)\geq r-j+1\)，\(i\)在\([l,r]\)中的字典序一定比\(j\)大。

所以可以得到，对于\(i\)，令\(j\)是\(i\)后边第一个\(rk_j>rk_i\)的位置，\(i\)会在\([i,j+LCP(i,j)-1]\)这个区间成为答案（用\(R[i]\)表示\(i\)做答案的这个区间的右端点）。

所以我们把询问按左端点排序，\(i\)从\(n\)到\(1\)倒着枚举，用单调栈维护这些可能成为答案的区间。

当枚举到\(i\)时，处理左端点为\(i\)的询问。所以单调栈的每个元素存三个值：\(L,R,p\)，表示当询问右端点在\([L,R]\)中时，答案为后缀\(p\)。

我们每加入一个\(i\)，它可能会覆盖掉后面几个区间成为最优解，如图：

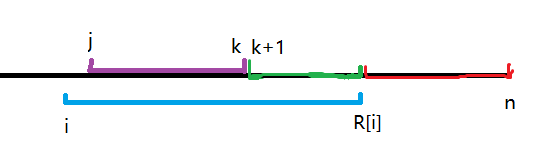
（此时单调栈中自底向上依次存的是红色、绿色、紫色区间）

拿紫色的线段为例（假设紫色线段是由\(j\)作为答案，\(k\)就是\(R[j]\)），此时无论询问右端点在点\(j\)还是在点\(k\)，后缀\(i\)都要比\(j\)更优（字典序更大，比较方式同前文所说），所以蓝色会覆盖紫色，直接把紫色线段弹出栈。同理判断蓝色完全覆盖绿色后也把绿色线段弹出栈。

然后在栈中加入元素：\(\{i,R[i],i\}\)（如前文所说的\(L,R,p\)）。

当然还会有这种情况：

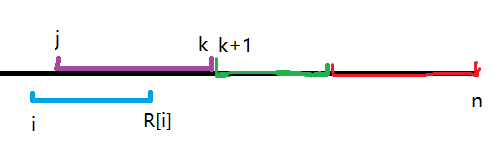
比如对于串oamodap，在\(i=2\)时\(4\)在右端点为\(4\sim5\)时会成为答案，而当\(i=1\)时，\(4\)只在右端点为\(5\)时成为答案，右端点为\(1\sim4\)时是\(1\)作为答案。

蓝色\(i\)在紫色\(j\)的某左半段区间中会作为答案。

也就是当右端点在点\(j\)处时，\(i\)比\(j\)更优；而右端点在点\(k\)时，还是\(j\)比\(i\)更优。

此时我们可以二分找到\(R[i]\)。就是判断右端点在哪个位置时，恰好使得后缀\(j\)比\(i\)更优（当然其实不需要二分，\(R[i]\)就是\(j+LCP(i,j)\)）。

记这个位置为\(p\)。然后我们把\(j\)影响的区间\([j,k]\)改为\([p,k]\)。

此时\(i\)所影响的区间就是\([i,p-1]\)（\(R[i]=p-1\)），所以在栈中加入元素\(\{i,p-1,i\}\)。

（\(x\)影响区间\([l,r]\)就是指询问右端点在\([l,r]\)中时\(x\)作为答案）

对于询问\([l,r]\)，此时\(l=i\)，而单调栈中的区间是有序的。所以在单调栈中二分\(r\)在哪段区间中就可以了。

复杂度\(O((n+q)\log n)\)。

//12640kb	1028ms
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define gc() getchar()
typedef long long LL;
const int N=1e5+5;

struct Node
{
	int l,r,p;
}sk[N];
struct Quries
{
	int id,l,r;
	inline bool operator <(const Quries &x)const
	{
		return l<x.l;
	}
}q[N];
struct Suffix_Array
{
	int tm[N],rk[N],sa[N],sa2[N],ht[N],Log[N],st[N][17];
	char s[N];

	inline void Init_ST(const int n)
	{
		for(int i=2; i<=n; ++i) Log[i]=Log[i>>1]+1;
		for(int i=1; i<=n; ++i) st[i][0]=ht[i];
		for(int j=1; j<=Log[n]; ++j)
			for(int t=1<<j-1,i=n-t; i; --i)
				st[i][j]=std::min(st[i][j-1],st[i+t][j-1]);
	}
	inline int LCP(int l,int r)
	{
		l=rk[l], r=rk[r]; if(l>r) std::swap(l,r);
		++l;
		int k=Log[r-l+1];
		return std::min(st[l][k],st[r-(1<<k)+1][k]);
	}
	int Build()
	{
		scanf("%s",s+1);
		const int n=strlen(s+1);
		int *x=rk,*y=sa2,m=300;
		for(int i=0; i<=m; ++i) tm[i]=0;
		for(int i=1; i<=n; ++i) ++tm[x[i]=s[i]];
		for(int i=1; i<=m; ++i) tm[i]+=tm[i-1];
		for(int i=n; i; --i) sa[tm[x[i]]--]=i;
		for(int k=1,p=0; k<n; k<<=1,m=p,p=0)
		{
			for(int i=n-k+1; i<=n; ++i) y[++p]=i;
			for(int i=1; i<=n; ++i) if(sa[i]>k) y[++p]=sa[i]-k;

			for(int i=0; i<=m; ++i) tm[i]=0;
			for(int i=1; i<=n; ++i) ++tm[x[i]];
			for(int i=1; i<=m; ++i) tm[i]+=tm[i-1];
			for(int i=n; i; --i) sa[tm[x[y[i]]]--]=y[i];

			std::swap(x,y), x[sa[1]]=p=1;
			for(int i=2; i<=n; ++i)
				x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?p:++p;
			if(p>=n) break;
		}
		for(int i=1; i<=n; ++i) rk[sa[i]]=i;
		ht[1]=0;
		for(int i=1,k=0,p; i<=n; ++i)
		{
			if(rk[i]==1) continue;
			if(k) --k;
			p=sa[rk[i]-1];
			while(i+k<=n && p+k<=n && s[i+k]==s[p+k]) ++k;
			ht[rk[i]]=k;
		}
		Init_ST(n);
		return n;
	}
}sa;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline bool Check(int i,int j,int r)
{
	return sa.rk[i]>sa.rk[j]||sa.LCP(i,j)>=r-j+1;
}

int main()
{
	static int Ans[N];
	const int n=sa.Build(),Q=read();
	for(int i=1; i<=Q; ++i) q[i]=(Quries){i,read(),read()};
	std::sort(q+1,q+1+Q); q[0].l=0, sk[0].l=n+1;
	int top=1,now=Q; sk[1]=(Node){n,n,n};
	while(q[now].l==n) Ans[q[now--].id]=n;
	for(int i=n-1; i; --i)
	{
		bool f=0;
		while(top)
		{
			if(Check(i,sk[top].p,sk[top].r)) --top;
			else if(Check(i,sk[top].p,sk[top].l)) {f=1; break;}
			else break;
		}
		if(f)
		{
//			int j=sk[top].p,l=sk[top].l,r=sk[top].r,mid;
//			while(l<r)
//			{
//				if(Check(i,j,mid=l+r>>1)) l=mid+1;
//				else r=mid;
//			}
//			sk[top].l=l;
			sk[top].l=sk[top].p+sa.LCP(i,sk[top].p);//这里不需要二分。。=-=
		}
		sk[++top]=(Node){i,sk[top-1].l-1,i};
		while(q[now].l==i)
		{
			int p=q[now].r,l=1,r=top,mid;
			while(l<=r)
			{
				mid=l+r>>1;
				if(p>=sk[mid].l && p<=sk[mid].r) break;
				else if(p>sk[mid].r) r=mid-1;
				else l=mid+1;
			}
			Ans[q[now--].id]=sk[mid].p;
		}
	}
	for(int i=1; i<=Q; printf("%d\n",Ans[i++]));

	return 0;
}