C++基础算法学习——汉洛塔问题

汉诺塔问题
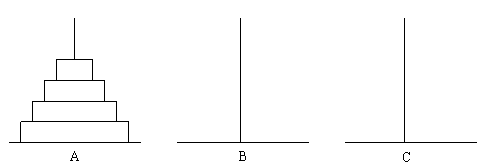
古代有一个梵塔,塔内有三个座A、B、C,A座上有64个盘子,盘子大小
不等,大的在下,小的在上(如图)。有一个和尚想把这64个盘子从A座移
到C座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子
始终保持大盘在下,小盘在上。在移动过程中可以利用B座,要求输出移动
的步骤 。

代码如下：

#include <iostream>

using namespace std;
void Hanota(int n,char a,char b,char c)
{
    if(n==)
    {
        cout<<a<<"-->"<<c<<endl;
        return;
    }
    Hanota(n-,a,c,b);
    Hanota(,a,b,c);
    Hanota(n-,b,a,c);
}
int main()
{
    int n;
    cout<<"请输入n的值：";
    cin>>n;
    Hanota(n,'a','b','c');
    return ;
}