MATLAB最小二乘法

MATLAB最小二乘法

作者：凯鲁嘎吉 - 博客园
http://www.cnblogs.com/kailugaji/

三、实验程序

四、实验内容

设有如下数据：

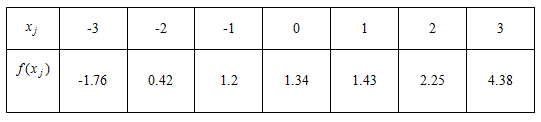
用3次多项式拟合这组数据.

五、解答（按如下顺序提交电子版）

1.(程序)

LSM1.m:

function p=LSM1(x,y,m)  %x,y为序列长度相等的数据向量，m为拟合多项式次数
format short;
A=zeros(m+1,m+1);
for i=0:m
    for j=0:m
        A(i+1,j+1)=sum(x.^(i+j));
    end
    b(i+1)=sum(x.^i.*y);
end
a=A\b';
p=fliplr(a');

2.(运算结果)

>> x=[-3,-2,-1,0,1,2,3];
>> y=[-1.76,0.42,1.2,1.34,1.43,2.25,4.38];
>> p=LSM1(x,y,3)

p =

    0.1133   -0.0018    0.0035    1.3300

3.(拓展（方法改进、体会等）)

MATLAB中有关于最小二乘法的现成的函数，如下编写程序：

ploy1.m：

function [p]=ploy1(x,y)
P=polyfit(x,y,3);
xi=-4:.2:4;
p=polyfit(x,y,3);
yi=polyval(P,xi);
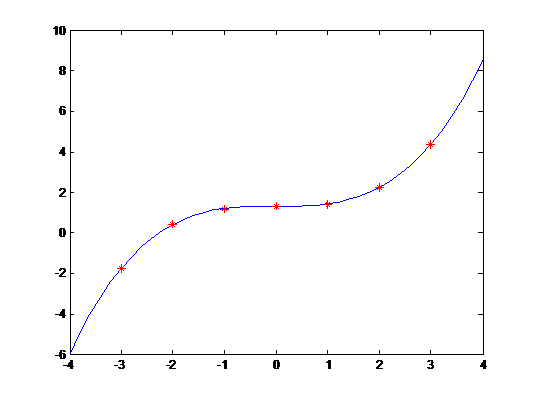
plot(xi,yi,x,y,'r*'); 

结果：

>> x=[-3,-2,-1,0,1,2,3];
y=[-1.76,0.42,1.2,1.34,1.43,2.25,4.38]; [p]=ploy1(x,y)

p =

    0.1133   -0.0018    0.0035    1.3300

则y=0.1133*x^3-0.0018*x^2+0.0035*x+1.33

注：非线性曲线拟合见：MATLAB实例：非线性曲线拟合