[HDU6146]Pokémon GO

Problem

有一个2n的方格矩阵

在一个格子上可以往旁边8个方向走（如果有格子），求有多少方案把2n走完

Solution

我们用Fi表示从一个角出发走遍所有格子回到这一列另外一点的方案数

显然,F1 = 1,Fn = 2 * Fn-1 = 2^(n-1)



我们再用Gi表示从一个角出发，走遍所有格子的方案数

那么Gi = Fi + 2 * Gi-1 + 4 * Gi-2



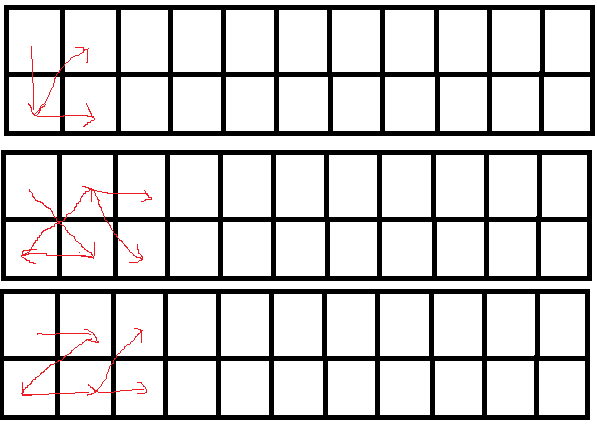
所以四个角出发的方案便为4Gn

我们再考虑从中间的列出发的方案：

每一列可以从上下两个格子出发，然后有2（2 * Fi * Gn−i + 2 * Fn−i+1 * Gi−1）种方案

Notice

要考虑全所有情况

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define sqz main
#define ll long long
#define reg register int
#define rep(i, a, b) for (reg i = a; i <= b; i++)
#define per(i, a, b) for (reg i = a; i >= b; i--)
#define travel(i, u) for (reg i = head[u]; i; i = edge[i].next)
const int INF = 1e9, N = 10000, mo = INF + 7;
const double eps = 1e-6, phi = acos(-1);
ll mod(ll a, ll b) {if (a >= b || a < 0) a %= b; if (a < 0) a += b; return a;}
ll read(){ ll x = 0; int zf = 1; char ch; while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;}
void write(ll y) { if (y < 0) putchar('-'), y = -y; if (y > 9) write(y / 10); putchar(y % 10 + '0');}
ll D[N + 5], E[N + 5];
int main()
{
	int T_T = read();
	D[1] = 1;
	rep(i, 2, N) D[i] = D[i - 1] * 2 % mo;
	E[0] = 0, E[1] = 1, E[2] = 6;
	rep(i, 3, N) E[i] = (D[i] + E[i - 1] * 2 + E[i - 2] * 4) % mo;
	rep(i, 1, T_T)
	{
		int n = read();
		if (n == 1)
		{
			puts("2");
			continue;
		}
		ll ans = E[n];
		rep(j, 2, n - 1) ans = (ans + D[j] * E[n - j] + D[n - j + 1] * E[j - 1]) % mo;
		write(ans * 4 % mo); puts("");
	}
}