dfs问题总结

组合总和——给定元素不重复

需求：给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例：candidates = [2,3,5], target = 8。结果[(2,2,2,2),(3,5)]

思路：

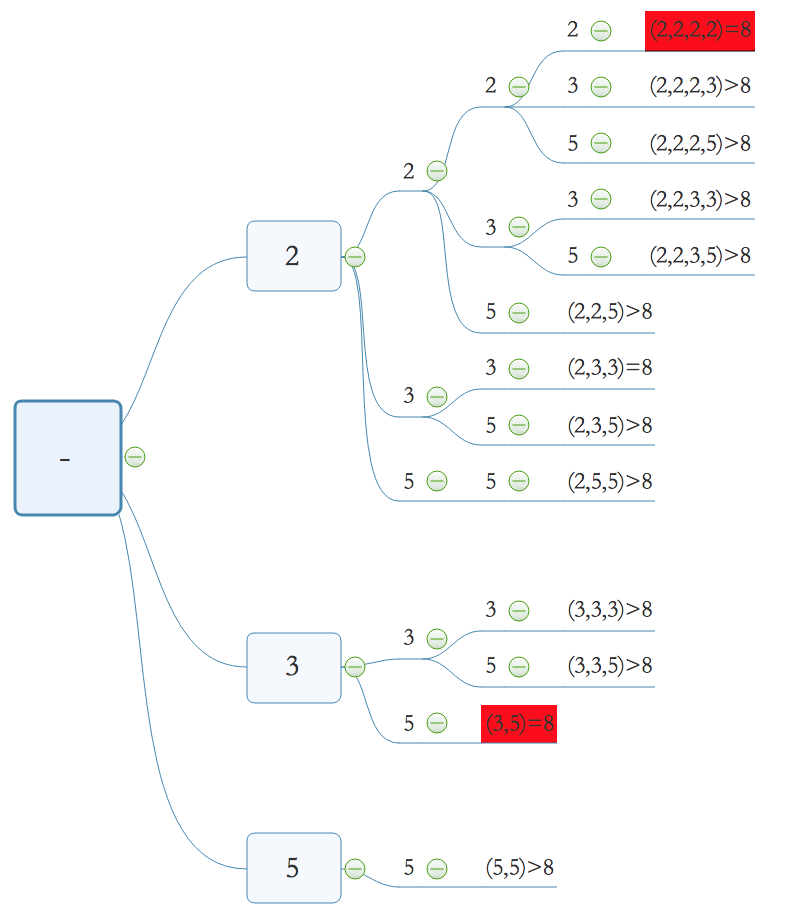
代码

public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(candidates);
        dfs(candidates, result, new ArrayList<>(), target, 0);
        return result;
    }

    void dfs(int[] candidates, List<List<Integer>> result, List<Integer> list, int target, int start) {
        if (target == 0) {
            result.add(new ArrayList<>(list));
        } else if (target > 0) {
            for (int i = start; i < candidates.length && candidates[i] <= target; ++i) {
                list.add(candidates[i]);
                dfs(candidates, result, list, target - candidates[i], i);
                list.remove(list.size() - 1);
            }
        }
    }

说明

1.为了不出现（2,3,5）,(3,2,5)这样的重合，每次dfs时起始元素为目前所处的位置：

dfs(candidates, result, list, target - candidates[i], i)

2.为了避免无谓的遍历，通过剪枝结束遍历：

candidates[i] <= target

组合总和——给定元素重复

需求：给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

• 所有数字（包括目标数）都是正整数。
• 解集不能包含重复的组合。

示例：candidates = [1,2,2,2,5], target = 5。结果[(1,2,2),(5)]

代码

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(candidates);
        dfs(candidates, result, new ArrayList<>(), target, 0);
        return result;
    }

    void dfs(int[] candidates, List<List<Integer>> result, List<Integer> list, int target, int start) {
        if (target == 0) {
            result.add(new ArrayList<>(list));
        } else if (target > 0) {
            for (int i = start; i < candidates.length && candidates[i] <= target; ++i) {
                if (i > start && candidates[i] == candidates[i - 1]) {
                    continue;
                }
                list.add(candidates[i]);
                dfs(candidates, result, list, target - candidates[i], i + 1);
                list.remove(list.size() - 1);
            }
        }
    }

组合总和3——指定个数

需求：找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例：输入: k = 3, n = 9，输出: [[1,2,6], [1,3,5], [2,3,4]]

代码

public List<List<Integer>> combinationSum3(int k, int n) {
        int[] candidate = {1,2,3,4,5,6,7,8,9};
        List<List<Integer>> result = new ArrayList<>();
        dfs(candidate, result, new ArrayList<>(), n, k, 0);
        return result;
    }
    void dfs(int[] candidate, List<List<Integer>> result, List<Integer> list, int target, int k, int start) {
        if (target == 0) {
            if (list.size() == k) {
                result.add(new ArrayList<>(list));
            }
        } else if (target > 0) {
            for (int i = start; i < candidate.length && candidate[i] <= target; ++i) {
                if (list.size() >= k) {
                    continue;
                }
                list.add(candidate[i]);
                dfs(candidate, result, list, target - candidate[i], k, i+1);
                list.remove(list.size() - 1);
            }
        }
    }