华容道 [NOIP 2013]

Describltion

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次

玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

Input

输入文件为 puzzle.in。

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

Output

输出文件名为 puzzle.out。

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

Sample Input

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

Sample Output

2
-1

Explanation

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

移动过程如下：

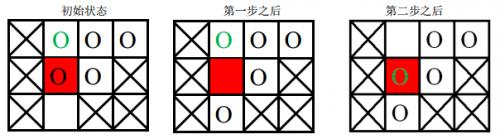
第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

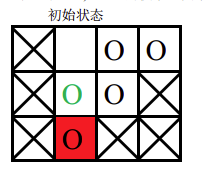
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。

Data Range

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

Solution

首先观察一下这道题，我们可以看出

　　1.不同棋子的移动，可以看成唯一的空格在移动

　　2.一个棋子要移动，旁边必须存在空格

所以我们可以知道，目标棋子要从起点开始移动，空格必须先移到它旁边。

然后目标棋子可以开始走了，但它走必须也要带着空格跑

所以记录状态的时候，必须把三个状态都记录下来，直到它到终点。

所以我们可以看出此题分为两个步骤：

1.空格移到目标棋子身旁

2.目标棋子带着空格从起点到终点

考虑一下搜索的复杂度限制，Q<=500,那么搜索的要限制在10w以内

显然第一遍是二维状态，一次bfs即可搞定，复杂度不超过n²

而第二遍有四个维度直接搞可能会T，所以要思考如何优化。

我们发现，空格只有4种有效走法：从某一个位置移到目标棋子相邻的其他三个格子上且不经过目标棋子，或者与目标棋子交换位置。

所以对应每一种状态之间的转换我们可以用一条边相连，最后跑一次从起点到终点的SPFA就行了。

这里记录状态有个小技巧，记录两个点，我们可以把它压缩一下，记录目标棋子的坐标，并用加上t=0，1，2，3分别代表空格在哪个方向，最后某一个状态的编号就可以表示成120x+4y+i

代码

#include<set>
#include<map>
#include<stack>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define RG register int
#define rep(i,a,b)    for(RG i=a;i<=b;i++)
#define per(i,a,b)    for(RG i=a;i>=b;i--)
#define ll long long
#define inf (1<<30)
#define maxn 35
#define maxm 38888
using namespace std;
int n,m,q,cnt;
int vis[maxm],dis[maxn][maxn],gra[maxn][maxn],d[maxm],head[maxm];
struct E{
    int v,next,val;
}edge[maxm];
struct P{
    int x,y;
    P operator + (const P &tmp)const{
        return (P){x+tmp.x,y+tmp.y};
    }
}dir[];
inline int read()
{
    int x=,f=;char c=getchar();
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
 
inline int check(P tmp)
{
    if(!gra[tmp.x][tmp.y]||dis[tmp.x][tmp.y])    return ;return ;
}
 
inline void add(int u,int v,int val)
{
    edge[++cnt].v=v,edge[cnt].val=val,edge[cnt].next=head[u],head[u]=cnt;
}
 
void bfs(int sx,int sy,int tx,int ty,int type)
{
    memset(dis,,sizeof(dis));dis[sx][sy]=;
    queue<P> que;que.push((P){sx,sy});
    P u,v;
    while(!que.empty())
    {
        u=que.front(),que.pop();
        rep(i,,)
        {
            v=u+dir[i];
            if(!check(v))    continue;
            if(v.x==tx&&v.y==ty)    continue;
            dis[v.x][v.y]=dis[u.x][u.y]+;que.push((P){v.x,v.y});
        }
    }
    if(type==)    return;
    u=(P){tx,ty};
    rep(i,,)
    {
        v=u+dir[i];
        if(v.x==sx&&v.y==sy)    continue;
        if(!dis[v.x][v.y])    continue;
        add(tx*+ty*+type,tx*+ty*+i,dis[v.x][v.y]-);
    }
    add(tx*+ty*+type,sx*+sy*+type^,);
}
 
void spfa(int sx,int sy)
{
    P u=(P){sx,sy},v;int vid;
    queue<int> qe;
    rep(i,,) d[i]=inf,vis[i]=;
    rep(i,,)
    {
        v=u+dir[i];vid=sx*+sy*+i;
        if(dis[v.x][v.y])    qe.push(vid),d[vid]=dis[v.x][v.y]-,vis[vid]=;
    }
    while(!qe.empty())
    {
        int x=qe.front();qe.pop();vis[x]=;
        for(int i=head[x];i;i=edge[i].next)
        {
            int y=edge[i].v,w=edge[i].val;
            if(d[y]>d[x]+w)
            {
                d[y]=d[x]+w;
                if(!vis[y])    qe.push(y),vis[y]=;
            }
        }
    }
}
 
void init()
{
    dir[]=(P){-,};dir[]=(P){,};dir[]=(P){,-};dir[]=(P){,};
    rep(i,,n)
        rep(j,,m)
        {
            if(!gra[i][j])    continue;
            if(gra[i-][j])    bfs(i-,j,i,j,);
            if(gra[i+][j])    bfs(i+,j,i,j,);
            if(gra[i][j-])    bfs(i,j-,i,j,);
            if(gra[i][j+])    bfs(i,j+,i,j,);
        }     
 
    rep(i,,q)
    {
        int ax=read(),ay=read(),bx=read(),by=read(),cx=read(),cy=read();
        if(bx==cx&&by==cy){puts("");continue;}
        bfs(ax,ay,bx,by,);
        spfa(bx,by);
        int ans=inf;
        rep(j,,) ans=min(ans,d[cx*+cy*+j]);
        if(ans==inf)    puts("-1");
        else printf("%d\n",ans);
 
    }
}
 
int main()
{
    n=read(),m=read(),q=read();
    rep(i,,n)    rep(j,,m)    gra[i][j]=read();
    init();
    return ;
}

题外话

在做这道题debug的时候，发现了一些莫名其妙的错误：在给vis[]数组清零之后，原本的head[]发生了改变？花了我一个小时的时间，终于发现了，我定义的大小比我用循环清零的次数要小！我以为我见鬼了，两个毫不相关的数组产生了干扰。应该是越界了清零到另一个数组去了，以后一定要小心这种错误！