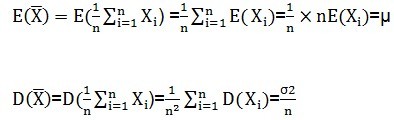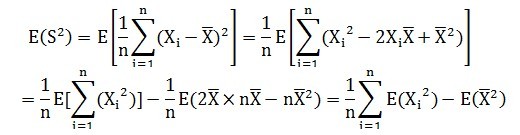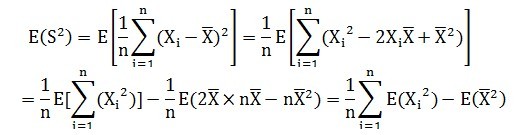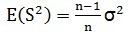样本方差的无偏估计与(n-1)的由来
一、无偏估计
所谓总体参数估计量的无偏性指的是,基于不同的样本,使用该估计量可算出多个估计值,但它们的平均值等于被估参数的真值。
在某些场合下,无偏性的要求是有实际意义的。例如,假设在某厂商与某销售商之间存在长期的供货关系,则在对产品出厂质量检验方法的选择上,采用随机抽样的方法来估计次品率就很公平。这是因为从长期来看,这种估计方法是无偏的。比如这一次所估计出来的次品率实际上偏高,厂商吃亏了;但下一次的估计很可能偏低,厂商的损失就可以补回来。由于双方的交往会长期多次发生,这时采用无偏估计,总的来说可以达到互不吃亏的效果。
不过,在某些场合中,无偏性的要求毫无实际意义。这里又有两种情况:一种情况是在某些场合中不可能发生多次抽样。例如,假设在某厂商和某销售商之间只会发生一次买卖交易,此后不可能再发生第二次商业往来。这时双方谁也吃亏不起,这里就没有什么“平均”可言。另一种情况则是估计误差不可能相互补偿,因此“平均”不得。例如,假设需要通过试验对一个批量的某种型号导弹的系统误差做出估计。这个时候,既使我们的估计的确做到了无偏,但如果这一批导弹的系统误差实际上要么偏左,要么偏右,结果只能是大部分导弹都不能命中目标,不可能存在“偏左”与“偏右”相互抵消,从而“平均命中”的概念。
由此可见,具有无偏性的估计量不一定就是我们“最需要”的“恰当”估计量。
无偏估计是参数的样本估计值的期望值等于参数的真实值。估计量的数学期望等于被估计参数,则称此为无偏估计。
设A'=g(X1,X2,...,Xn)是未知参数A的一个点估计量,若A'满足 E(A')= A 则称A'为A的无偏估计量,否则为有偏估计量。
注:无偏估计就是系统误差为零的估计。
由于公式A'=g(X1,X2,...,Xn)中的X1,X2,...,Xn一般为一次抽样的结果,没有明确是怎么抽样的一个过程,所以导致不好理解为什么A'就是A的无偏估计量,特别是很难举出实例来给与证明。
经过自己的查阅资料和理解,实际上无偏估计量可以理解如下:
简单的理解,无偏估计量就是:在样本中进行n次随机的抽样,每次抽样都可以计算出一个对某一个参数的点估计量,计算n次,得到n个点估计量,然后对n个点估计量计算期望,得到的值和需要估计的总体参数相等,则称n中的任何点估计量为总体参数的无偏估计量。
举例:
比如我要对某个学校一个年级的上千个学生估计他们的平均水平(真实值,上帝才知道的数字),那么我决定抽样来计算。
我抽出一个10个人的样本,可以计算出一个均值。那么如果我下次重新抽样,抽到的10个人可能就不一样了,那么这个从样本里面计算出来的均值可能就变了,对不对?
因为这个均值是随着我抽样变化的,而我抽出哪10个人来计算这个数字是随机的,那么这个均值也是随机的。但是这个均值也会服从一个规律(一个分布),那就是如果我抽很多次样本,计算出很多个这样的均值,这么多均值们的平均数应该接近上帝才知道的真实平均水平。
如果你能理解“样本均值”其实也是一个随机变量,那么就可以理解为这个随机变量的期望是真实值,所以无偏(这是无偏的定义);而它又是一个随机变量,只是估计而不精确地等于,所以是无偏估计量。
二、计算
假设X为独立同分布的一组随机变量,总体为M,随机抽取N个随机变量构成一个样本,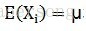
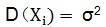
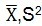
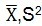
既然是随机变量,就可以观察他们的均值方差。
这里需要注意的是,由于样本是随机的,所以X1,X2,X3...都是随机的。上式中可以看出,样本均值这个变量的期望就是总体的均值,因此可以说均值是无偏的。
接下来看样本方差的均值:
根据方差公式,可以得到:
因此:
这里可以看出样本方差的期望并不是无偏的,要无偏估计,应该再乘上一个系数:
所以无偏估计的样本的方差:
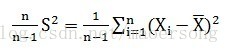
n-1既为自由度,就是说,在一个容量为n的样本里,当确定了n-1个变量以后,第n个变量就确定了,因为样本均值是无偏的。
协方差除以n-1原理和方差一样,因为方差为协方差的特殊情况。
参考:
http://www.cnblogs.com/gczr/p/8250272.html
https://blog.csdn.net/yangzhenzhen/article/details/73244592
样本方差的无偏估计与(n-1)的由来的更多相关文章
- kalman滤波(二)---扩展kalman滤波[EKF]的推导
一.状态估计的解释 我们知道每个方程都受噪声的影响,这里把位姿x和路标y看成服从某种概率分布的随机变量.因此我们关心的问题就变成了:当我们已知某些运动数据u和观测数据z时,如何确定状态量x,y的分布? ...
- 方差(variance)、标准差(Standard Deviation)、均方差、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)
方差(variance).标准差(Standard Deviation).均方差.均方根值(RMS).均方误差(MSE).均方根误差(RMSE) 2017年10月08日 11:18:54 cqfdcw ...
- 为什么样本方差的分母是n-1?为什么它又叫做无偏估计?
为什么样本方差的分母是n-1?最简单的原因,是因为因为均值已经用了n个数的平均来做估计在求方差时,只有(n-1)个数和均值信息是不相关的.而你的第n个数已经可以由前(n-1)个数和均值 来唯一确定,实 ...
- 为什么样本方差(sample variance)的分母是 n-1?
为什么样本方差(sample variance)的分母是 n-1? (補充一句哦,題主問的方差 estimator 通常用 moments 方法估計.如果用的是 ML 方法,請不要多想不是你們想的那樣 ...
- 为什么样本方差分母是n-1
https://blog.csdn.net/qq_39521554/article/details/79633207 为什么样本方差的分母是n-1?为什么它又叫做无偏估计? 至于为什么是n-1,可以看 ...
- 为什么样本方差除以(n-1)而不是n ?(自由度)
不记得第几次看见样本方差的公式,突然好奇为什么要除以(n-1)而不是n呢?看见一篇文章从定义上和无偏估计推导上讲的很清楚https://blog.csdn.net/fuming2021118535/a ...
- 为什么样本方差自由度(分母)为n-1
一.概念.条件及目的 1.概念 要理解样本方差的自由度为什么是n-1,得先理解自由度的概念: 自由度,是指附加给独立的观测值的约束或限制的个数,即一组数据中可以自由取值的个数. 2.成立条件 所谓自由 ...
- Java名字的由来
Java语言的历程丰富多彩,被现在众多程序员和企业广泛使用,不用质疑这是Java的领先技术的结果. Java是Sun公司开发的一种编程语言,Sun公司最初的方向是让Java来开发一些电器装置程序,如: ...
- Python的由来
Python的由来 Python这门语言是由C开发而来. C语言: 代码编译得到 机器码 ,机器码在处理器上直接执行,每一条指令控制CPU工作 其他语言: 代码编译得到 字节码 ,虚拟机执行字节码并转 ...
随机推荐
- Django入门--模型系统(二):常用查询及表关系的实现
1.常用查询 模型类上的管理器: ** 模型类.objects ** (1)常用一般查询 rs = Student.objects.all() # 查询所有记录,返回Queryset print(rs ...
- 干货:鲜为人用的MySQL高级特性与玩法!
上一篇文章<万字总结:学习MySQL优化原理,这一篇就够了!>文末给大家留有两个开放的问题: 有非常多的程序员在分享时都会抛出这样一个观点:尽可能不要使用存储过程,存储过程非常不容易维护, ...
- spring的几个重要类和接口
1.datasource接口是javax.sql包下的接口,不是spring,是javax.sql下的 datasource接口有个重要的方法getConnection()方法 Connection ...
- Codeforces Round #260 (Div. 1)——Civilization
题目链接 题意: n个点,m条边的森林.q次操作. 每次操作:1.询问x所在树的直径 2.合并x和y所在的树,使得合并后的直径最小 ) 分析: 没有读到图是森林.. .做的好纠结 最開始将每一个树都求 ...
- Log使用
学习参考:http://blog.csdn.net/hu_shengyang/article/details/6754031 log4j三种主要组件: logger记录对象 appender输出对象 ...
- PHP生成二维码的2种方式
二维码的用处俺也就不说了,看一下用PHP生成的二维码吧. 利用谷歌提供的API 生成二维码,如今非常多国外站点都提供了这类API 看下代码吧<=======================> ...
- lvs 负载均衡环境搭建
记录一下搭建lvs环境的步骤 当中master 10.0.0.11,backup 10.0.0.15.realserver1 10.0.0.119.realserver210.0.0.11 1.mkd ...
- 服务器未能识别http头soapaction的值
公司真是坑的一比 ,连接PDA报出这个错误 网上找的解决方案: 加什么wsdl http://www.cnblogs.com/dengxinglin/archive/2012/05/02/247868 ...
- 制作ubuntu的U盘启动盘
在制作U盘启动盘之前,请各位先格式化你的U盘. 制作U盘启动盘的工具有很多种,我们这里为大家介绍的是用软碟通制作.所有我们需要有这个软件,如果大家没有可以百度“软碟通”,下载安装一个.然后点击打开.在 ...
- 杂文 | 金沙江创投朱啸虎谈微信小程序
我一直在想怎么去描述和朱啸虎的聊天. 最简单的开头一定是说“独角兽捕手朱啸虎”看好小程序了,这个赛道蕴含了许多无比巨大.充沛的机会,所以约到朱啸虎同学深聊这个赛道的创业.但是这样的开头太平,不好玩.事 ...