HDU 2604 Queuing，矩阵高速幂

题目地址：HDU 2604 Queuing

题意： 

略

分析：

易推出:   f(n)=f(n-1)+f(n-3)+f(n-4)

构造一个矩阵：

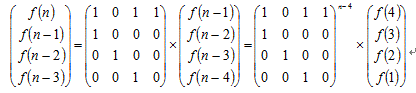
然后直接上板子：

/*
f[i] = f[i-1] + f[i-3] + f[i-4]

*/

#include<cstdio>
#include<cstring>

using namespace std;

const int N = 4;
int L, M;

struct mtx
{
    int x[N+1][N+1];
    mtx(){
        memset(x, 0, sizeof x );
    }
};

mtx operator *(const mtx &a, const mtx &b){
    mtx c;
    for(int i=0; i<N; ++i)
    {
        for(int j=0; j<N; ++j)
        {
            for(int k=0; k<N; ++k)
            {
                c.x[i][j] = (c.x[i][j] + a.x[i][k]*b.x[k][j]) % M;
            }
        }
    }
    return c;
}

mtx operator ^(mtx a, int n)
{
    mtx res;
    for(int i=0; i<N; ++i) res.x[i][i] = 1;
    for(; n; n>>=1)
    {
        if(n&1) res = res * a;
        a = a * a;
    }
    return res;
}

int f[N+1];
mtx I;

void init()
{
    f[1] = 2;
    f[2] = 4;
    f[3] = 6;
    f[4] = 9;
    I.x[0][0] = I.x[0][2] = I.x[0][3] = I.x[1][0]
              = I.x[2][1] = I.x[3][2] = 1;
}

void work()
{
    if(L<=4){
        printf("%d\n", f[L] % M);
        return ;
    }
    mtx res = I^(L-4);
    int F_n = 0;
    for(int i=0; i<N; ++i)
    {
        F_n = (F_n + res.x[0][i]*f[N-i] ) % M;
    }
    printf("%d\n", F_n);
}
int main()
{
    init();
    while(~scanf("%d%d", &L, &M))
    {
        work();
    }
    return 0;
}