特征描述子（feature descriptor） —— HOG（方向梯度直方图）

HOG（Histogram of Oriented Gradients），描述的是图像的局部特征，其命名也暗示了其计算方法，先计算图像中某一区域不同方向上梯度的值，然后累积计算频次，得到直方图，该直方图便可代表该区域了，也即从图像中抽取得到的特征向量，可以作为后续分类器的输入了。

注意，HOG 刻画的是图像的局部特征，对于一副高分辨率图像当然可以直接提取特征，效果并不理想。从信息论的角度说，一幅 640*480 的图像，约有 30 万个像素点，直接对原始图像做 HOG 特征提取的话，按照 360°，分成 360 个bins，HOG 没有表示这么大一副图像的能力。从特征工程的角度看，一般来说，只有图像区域比较小的情况，基于统计原理的直方图对于该区域才有表达能力（表达能力即为区别能力），如果图像区域比较大，那么两个完全不同的图像的HOG特征，也可能很相似。但是如果区域较小，这种可能性就很小。最后，把图像分割成很多区块，然后对每个区块计算HOG特征，这也包含了几何（位置）特性。例如，正面的人脸，左上部分的图像区块提取的HOG特征一般是和眼睛的HOG特征符合的。

1. 算法流程

• 图像分块 ⇒ patches

• 利用任意一种梯度算子，sobel、laplacian等，对每一个 patch 进行卷积，计算得到像素点的梯度方向和幅值：

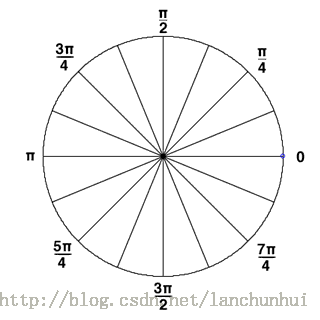
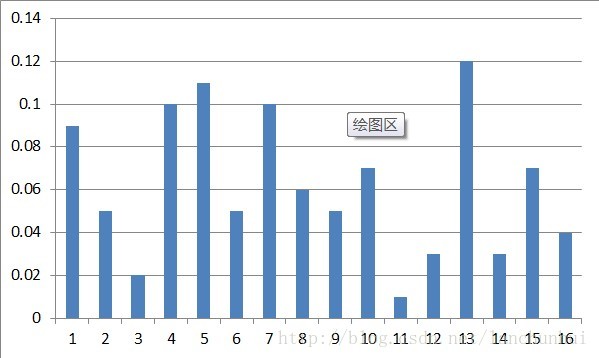
  Mx,y=I2x+I2y−−−−−−√θ(x,y)=tan−1IyIx,∈[0,360°)/[0,180°)

• 将 360° 分成若干个 bins，例如均分为 16 个 bins，如下：

  
  
  

references

• Histogram of Oriented Gridients(HOG) 方向梯度直方图
• 方向梯度直方图（HOG,Histogram of Gradient）学习笔记二 HOG正篇
• skimage 给出的 HOG 实现