P1228 地毯填补问题（分治）

题目描述

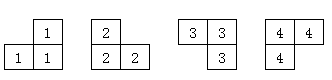
相传在一个古老的阿拉伯国家里，有一座宫殿。宫殿里有个四四方方的格子迷宫，国王选择驸马的方法非常特殊，也非常简单：公主就站在其中一个方格子上，只要谁能用地毯将除公主站立的地方外的所有地方盖上，美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住，毯子的形状有所规定，只能有四种选择(如图4-l)：

并且每一方格只能用一层地毯，迷宫的大小为(2k)^2的方形。当然，也不能让公主无限制的在那儿等，对吧？由于你使用的是计算机，所以实现时间为1s。

输入输出格式

输入格式：

输入文件共2行。

第一行：k，即给定被填补迷宫的大小为2^k(0<k≤10)；

第二行：x y，即给出公主所在方格的坐标(x为行坐标，y为列坐标)，x和y之间有一个空格隔开。

输出格式：

将迷宫填补完整的方案：每一补(行)为x y c (x，y为毯子拐角的行坐标和列坐标，c为使用毯子的形状，具体见上面的图1，毯子形状分别用1、2、3、4表示，x、y、c之间用一个空格隔开)。

输入输出样例

输入样例#1：复制

3

3 3

输出样例#1：复制

说明

事实上感觉四个的形状分别是这样（仅供参考，如果有问题联系icy）

spj报错：

1:c 越界

2:x,y 越界

3:mp[x][y] 已被占用

4:mp[x][y] 从未被使用

题解：

初看这个问题，似乎无从下手，于是我们可以先考虑最简单的情况，既n = 2时

0 0 0 1 这时，无论公主在哪个格子，我们都可以用一块毯子填满

继续考虑n = 4的情况

我们已经知道了解决2 * 2的格子中有一个障碍的情况如何解决，因此我们可以尝试构造这种情况

首先，显然可以将4 4的盘面划分成4个2 2的小盘面，其中一块已经存在一个障碍了

而我们只需在正中间的2 * 2方格中放入一块地毯，就可以使所有小盘面都有一个障碍

于是，n = 4的情况就解决了

我们可以将n = 4时的解法可以推广到一般情况，既当n = 2 k时，我们均可以将问题划分为4个n = 2 k – 1的子问题，然后分治解决即可。

下面附上代码（算法：分治）：

 #include<cstdio>

 typedef long long ll;

 ll x,y,len; int k;

 ll fun(int k)

 {

     ll sum=;

     for(int i=;i<=k;++i) sum*=;

     return sum;

 }

 void solve(ll x,ll y,ll a,ll b,ll l)

 {

     if(l==) return;

     if(x-a<=l/- && y-b<=l/-)

     {

         printf("%lld %lld 1\n",a+l/,b+l/);

         solve(x,y,a,b,l/);

         solve(a+l/-,b+l/,a,b+l/,l/);

         solve(a+l/,b+l/-,a+l/,b,l/);

         solve(a+l/,b+l/,a+l/,b+l/,l/);

     }

     else if(x-a<=l/- && y-b>l/-)

     {

         printf("%lld %lld 2\n",a+l/,b+l/-);

         solve(a+l/-,b+l/-,a,b,l/);

         solve(x,y,a,b+l/,l/);

         solve(a+l/,b+l/-,a+l/,b,l/);

         solve(a+l/,b+l/,a+l/,b+l/,l/);

     }

     else if(x-a>l/- && y-b<=l/-)

     {

         printf("%lld %lld 3\n",a+l/-,b+l/);

         solve(a+l/-,b+l/-,a,b,l/);

         solve(a+l/-,b+l/,a,b+l/,l/);

         solve(x,y,a+l/,b,l/);

         solve(a+l/,b+l/,a+l/,b+l/,l/);

     }

     else

     {

         printf("%lld %lld 4\n",a+l/-,b+l/-);

         solve(a+l/-,b+l/-,a,b,l/);

         solve(a+l/-,b+l/,a,b+l/,l/);

         solve(a+l/,b+l/-,a+l/,b,l/);

         solve(x,y,a+l/,b+l/,l/);

     }

 }

 int main()

 {

     scanf("%d %lld %lld",&k,&x,&y);

     len=fun(k);

     solve(x,y,,,len);

     return ;

 }