机器学习算法--Perceptron(感知机)算法

感知机：

假设输入空间是\(\chi\subseteq R^n\),输出空间是\(\gamma =\left( +1,-1\right)\)。输入\(\chi\in X\)表示实例的特征向量，对应于输入空间的点；输出\(y\in \gamma\)表示实例的类别。由输入空间到输出空间的如下函数：

\[f\left( x\right) =sign\left( wx+b\right)
\]

称为感知机。其中，w和b为感知机模型的参数，sign是符号函数，即：

\[sign\left( x\right) =\begin{cases}+1 &x\geq 0\\-1 &x<0 \end{cases}
\]

感知机学习策略

假设训练数据集是线性可分的，感知机学习的目标就是求得一个能够将训练集正实例点和负实例点完成正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型参数w，b，需定义损失函数并将损失函数极小化。

损失函数使用误分类点到超平面S的总距离，因此输入空间\(R^n​\)中任何一点\(x_0​\)到超平面S的距离为：

\[\dfrac {1}{\left\| w\right\| }\left| wx+b\right|
\]

在这里，\(\left\| w\right\|\)是w的\(L_2\)范数。

对于误分类的数据\(\left(x_i,y_i\right)\)来说，

\[-y_i( wx_i+b) >0
\]

成立。因为当\(wx_i + b >0\)时，\(y_i=-1\)，而当\(wx_i + b < 0\)时，\(y_i=+1\)，因此，误分类点\(x_i\)到超平面S的距离是:

\[-\dfrac {1}{\left\| w\right\| }y_i( wx_i+b)
\]

这样，假设超平面S的误分类点集合为M，那么所以误分类点到超平面S的总距离为：

\[-\dfrac {1}{\left\| w\right\| }\sum _{x_{i} \in M}y_{i}\left( wx_{i}+b\right)
\]

不考虑\(\dfrac {1}{\left\| w\right\| }\)，就得到感知机学习的损失函数：

\[L\left( w,b\right) =-\sum _{x_{i\varepsilon }n}y_i\left(wx_i+b\right)
\]

其中M为误分类点的集合。

感知机算法原始形式

感知机算法是使得损失函数\(L(w,b)\)极小化的最优化问题，可以使用随机梯度下降法来进行最优化。

假设误分类点集合M是固定的，那么损失函数\(L(w,b)\)的梯度由

\[\nabla _{w}L\left( \omega ,b\right) =-\sum _{x_{i\varepsilon }n}y_{i}x_{i}
\]

\[\nabla _{b}L\left( \omega ,b\right) =-\sum _{x_{i\varepsilon }n}y_{i}
\]

给出，随机选取一个误分类点\((x_i,y_i)\)，对w，b进行更新：

\[w\leftarrow w+\eta y_ix_i
\]

\[b\leftarrow b+\eta y_i
\]

其中\(\eta(0<\eta \leq1)\) 称为学习率(learning rate)，这样通过迭代可以使得损失函数\(L(w,b)\)不断减小，直到为0。

感知机算法原始形式的主要训练过程：

def trainPerceptron(dataMat, labelMat, eta):
    m, n = dataMat.shape
    weight = np.zeros(n)
    bias = 0

    flag = True
    while flag:
        for i in range(m):
            if np.any(labelMat[i] * (np.dot(weight, dataMat[i]) + bias) <= 0):
                weight = weight + eta * labelMat[i] * dataMat[i].T
                bias = bias + eta * labelMat[i]
                print("weight, bias: ", end="")
                print(weight, end="  ")
                print(bias)
                flag = True
                break
            else:
                flag = False

    return weight, bias

完整代码可以前往我的github查看，还有可视化过程。

https://github.com/yangliu0/MachineLearning/tree/master/Perceptron

感知机算法的对偶形式

假设\(w_0，b_0\)均初始化为0，对误分类点通过

\[w\leftarrow w+\eta y_ix_i
\]

\[b\leftarrow b+\eta y_i
\]

逐步修改\(w，b\)，设修改n次，则\(w，b\)关于\((w_i,y_i)\)的增量分为是\(\alpha_i y_ix_i\)和\(\alpha_i y_i\)，这里的\(\alpha_i=n_i \eta\)，其中\(n_i\)表示第i个点误分类的次数，这样最后学习到的\(w,b\)可以分别表示为

\[w=\sum ^{N}_{i=1}\alpha _{i}y_{i}x_{i}
\]

\[b=\sum ^{N}_{i=1}\alpha _{i}y_{i}
\]

实例点更新的次数越多，意味着它距离分离超平面越近，也就越难正确分类。

训练过程：输出\(\alpha,b\)，其中\(\alpha = (\alpha_1, \alpha_2,...,\alpha_N)^T\)

(1)\(\alpha\leftarrow0, b\leftarrow0\)

(2)在训练集中选取数据\((x_i, y_i)\)

(3)如果\(y_{i}\left( \sum ^{n}_{j=1}\alpha _{j}y_{j}x_{j}\cdot x_{i}+b\right)\leq0\)，则

\[\alpha_i \leftarrow\alpha_i + \eta
\]

\[b\leftarrow b+\eta y_i
\]

(4)转到(2)，直到没有错误。

最后通过\(w=\sum ^{N}_{i=1}\alpha _{i}y_{i}x_{i}\)计算出\(w\)，使用上述过程求出的\(b\)，即计算出模型参数。

以下就是上述感知机对偶形式的python训练代码：

def trainModel(dataMat, labelMat, alpha, b, eta):
    flag = True
    while flag:
        for i in range(m):
            if (labelMat[i, 0] * (np.sum((alpha * labelMat * np.dot(dataMat, dataMat[i].T).reshape((m, 1)))) + b)) <= 0:
                alpha[i] = alpha[i] + eta
                b = b + eta * labelMat[i]
                flag = True
                break
            else:
                flag = False
    w = np.dot(dataMat.T, alpha * labelMat)
    return w, b

以下就是结果可视化图，可以看出，训练的感知机算法对线性可分的点进行了很好的划分。

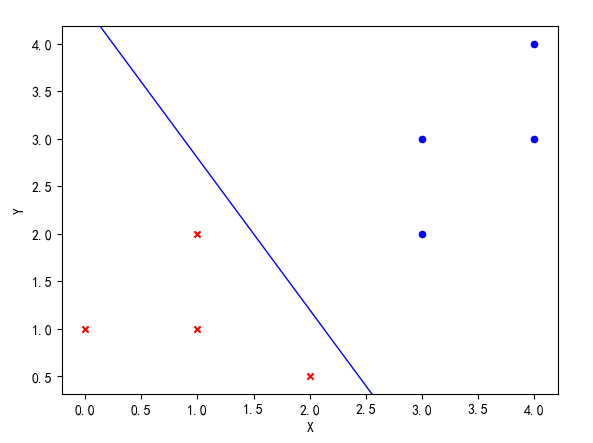
感知机算法的原始形式和对偶形式分别对应了支持向量机(SVM)的两种相应形式，是它们的基础。

上述两种形式的感知机算法完整实现可以在我的github查看，使用python实现。

https://github.com/yangliu0/MachineLearning/tree/master/Perceptron

参考文献

[1]统计学习方法.李航